Giải SGK Bài 7 Gia tốc – Chuyển động thẳng biến đổi đều Chương 3 Vật lí 10 Chân trời sáng tạo
Trong bài viết này HocThatGioi sẽ cùng bạn đi tìm đáp án và phương pháp tốt nhất giải quyết toàn bộ các câu hỏi và bài tập trong bài Gia tốc – Chuyển động thẳng biến đổi đều. Các bài tập sau đây thuộc Bài 7 Chương 3 ở các trang 40,41,42,…,47 Vật lí 10 Chân trời sáng tạo. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải SGK Câu hỏi mở đầu trang 40 Vật lí 10 Chân trời sáng tạo

Đại lượng đặc trưng cho sự thay đổi vận tốc của xe là gia tốc.
Giải SGK Mục 1 trang 40,41,42,43,44 Vật lí 10 Chân trời sáng tạo
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi luyện tập và vận dụng ở Mục 1 của các trang 40,41,42,43,44,45 trong bài Gia tốc – Chuyển động thẳng biến đổi đều ở ngay bên dưới nhé!
Giải SGK Câu hỏi 1 trang 40
Biểu thức tính vận tốc tức thời là: $v = \frac {d} {t}$
Để xác định được vận tốc tức thời, ta cần đo được độ dịch chuyển trong những khoảng thời gian ngắn bằng nhau.
Giải SGK Câu hỏi 2 trang 41
Chọn gốc tọa độ và gốc thời gian tại vị trí cổng quang điện A.
Giải SGK Câu hỏi 3 trang 41
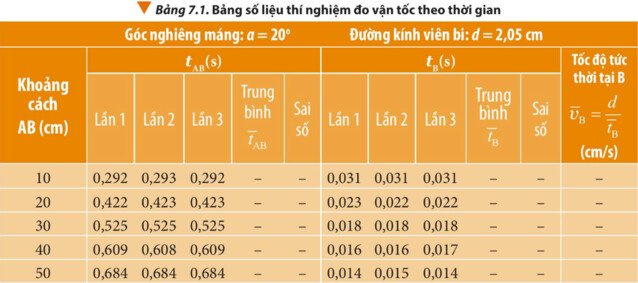
Biểu thức tính thời gian trung bình: $\bar{t}=\frac{t_1+t_2+\ldots+t_n}{n}$
Sai số tuyệt đối: $\Delta t_i=\left|\bar{t}-t_i\right|$
Sai số tuyệt đối trung bình của n lần đo: $\overline{\Delta t}=\frac{\Delta t_1+\Delta t_2+\ldots+\Delta t_n}{n}$
– Giá trị trung bình thời gian của viên bi chuyển động từ A đến B là:
$\begin{aligned} & +\mathrm{AB}=10 \mathrm{~cm}: \bar{t}=\frac{0,292+0,293+0,292}{3} \approx 0,292(\mathrm{~s}) \\ & +\mathrm{AB}=20 \mathrm{~cm}: \bar{t}=\frac{0,422+0,423+0,423}{3} \approx 0,423(\mathrm{~s}) \\ & +\mathrm{AB}=30 \mathrm{~cm}: \bar{t}=\frac{0,525+0,525+0,525}{3}=0,525(\mathrm{~s}) \\ & +\mathrm{AB}=40 \mathrm{~cm}: \bar{t}=\frac{0,609+0,608+0,609}{3} \approx 0,609(\mathrm{~s}) \\ & +\mathrm{AB}=50 \mathrm{~cm}: \bar{t}=\frac{0,609+0,608+0,609}{3} \approx 0,609(\mathrm{~s})\end{aligned}$
– Sai số của phép đo thời gian viên bi chuyển động từ A đến B:
+ AB = 10 cm:
$\begin{aligned} & \Delta t_1=|0,292-0,292|=0 \\ & \Delta t_2=|0,293-0,292|=0,001 \\ & \Delta t_3=|0,292-0,292|=0 \\ & \Rightarrow \overline{\Delta t}=\frac{0,001}{3} \approx 3,33.10^{-4}(s)\end{aligned}$
Tương tự cho các đoạn còn lại, ta có:
$\begin{aligned} & +\mathrm{AB}=20 \mathrm{~cm}: \overline{\Delta t}=3,33.10^{-4}(\mathrm{~s}) \\ & +\mathrm{AB}=30 \mathrm{~cm}: \overline{\Delta t}=0 \\ & +\mathrm{AB}=40 \mathrm{~cm}: \overline{\Delta t}=3,33.10^{-4}(\mathrm{~s}) \\ & +\mathrm{AB}=50 \mathrm{~cm}: \overline{\Delta t}=0\end{aligned}$
– Giá trị trung bình và sai số của thời gian chắn cổng quang điện tại B:
$\begin{aligned} & +\mathrm{AB}=10 \mathrm{~cm}: \bar{t}=0,031 ; \overline{\Delta t}=0 \\ & +\mathrm{AB}=20 \mathrm{~cm}: \bar{t}=0,022 ; \overline{\Delta t}=3,33.10^{-4} \\ & +\mathrm{AB}=30 \mathrm{~cm}: \bar{t}=0,018 ; \overline{\Delta t}=0 \\ & +\mathrm{AB}=40 \mathrm{~cm}: \bar{t}=0,016 ; \overline{\Delta t}=3,33.10^{-4} \\ & +\mathrm{AB}=50 \mathrm{~cm}: \bar{t}=0,014 ; \overline{\Delta t}=3,33.10^{-4}\end{aligned}$
– Tốc độ tức thời tại B:
$\begin{aligned} & +\mathrm{AB}=10 \mathrm{~cm}: \overline{v_B}=\frac{d}{\overline{t_B}}=\frac{10}{0,031} \approx 322,58(\mathrm{~cm} / \mathrm{s}) \\ & +\mathrm{AB}=20 \mathrm{~cm}: \overline{v_B}=\frac{d}{\overline{t_B}}=\frac{20}{0,022} \approx 909,09(\mathrm{~cm} / \mathrm{s}) \\ & +\mathrm{AB}=30 \mathrm{~cm}: \overline{v_B}=\frac{d}{\overline{t_B}}=\frac{30}{0,018} \approx 1666,67(\mathrm{~cm} / \mathrm{s}) \\ & +\mathrm{AB}=40 \mathrm{~cm}: \overline{v_B}=\frac{d}{\overline{t_B}}=\frac{40}{0,016}=2500(\mathrm{~cm} / \mathrm{s}) \\ & +\mathrm{AB}=50 \mathrm{~cm}: \overline{v_B}=\frac{d}{\overline{t_B}}=\frac{50}{0,014} \approx 3571,43(\mathrm{~cm} / \mathrm{s})\end{aligned}$
– Vẽ đồ thị:
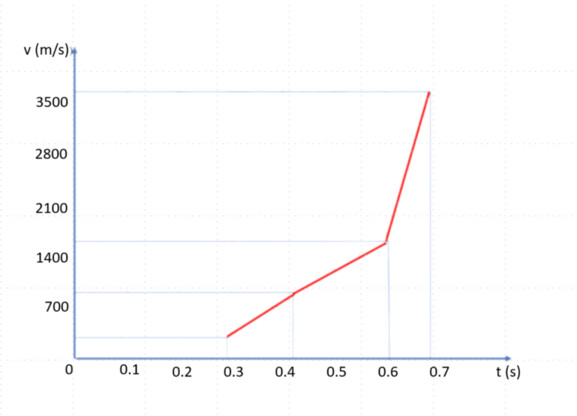
Giải SGK Câu hỏi 4 trang 42
– Một tàu hỏa bắt đầu xuất phát từ nhà ga và chuyển động nhanh dần
– Một viên bi rơi từ trên cao xuống dưới, chuyển động nhanh dần
– Một xe máy đang đi trên đường, gặp vật cản thì phanh gấp
Giải SGK Luyện tập trang 42
– Tính chất chuyển động của xe: xe đang chuyển động đều thì gặp chướng ngại vật, xe chuyển động chậm dần
– Mối liên hệ về hướng của vận tốc và gia tốc
+ Bắt đầu rời bến, xe chuyển động đều: a và v cùng hướng
+ Xe chuyển động chậm dần đều: a và v cùng phương nhưng ngược chiều.
Giải SGK Vận dụng trang 42
Trong chuyển động thẳng biến đổi đều được chia làm hai loại:
– Chuyển động thẳng nhanh dần đều, vận tốc tăng đều theo thời gian, $\overrightarrow{\mathbf{a}}$ và $\overrightarrow{\mathbf{v}}$ cùng chiều.
-Chuyển động thẳng chậm dần đều, vận tốc giảm đều theo thời gian, $\overrightarrow{\mathbf{a}}$ và $\overrightarrow{\mathbf{v}}$ ngược chiều.
Nếu $\overrightarrow{\mathbf{a}}$ và $\overrightarrow{\mathbf{v}}$ cùng chiều thì xe đi nhanh hơn do xe được tác dụng thêm một lực cùng chiều với hướng chuyển động của xe và ngược lại nếu $\overrightarrow{\mathbf{a}}$ và $\overrightarrow{\mathbf{v}}$ ngược chiều thì xe sẽ bị một lực cản trở làm xe đi chậm hơn.
Giải SGK Câu hỏi 5 trang 43
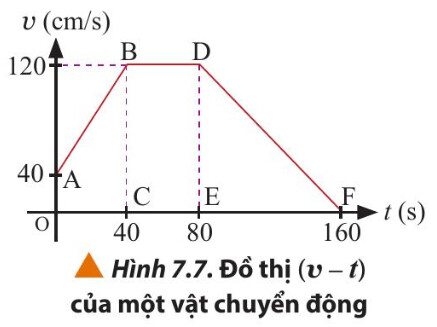
Quan sát hình vẽ
+ Độ dốc đi lên, vận tốc tăng dần theo thời gian, vật chuyển động nhanh dần đều
+ Độ dốc nằm ngang, vận tốc không thay đổi theo thời gian, vật chuyển động thẳng đều
+ Độ dốc đi xuống, vận tốc giảm dần theo thời gian, vật chuyển động chậm dần đều.
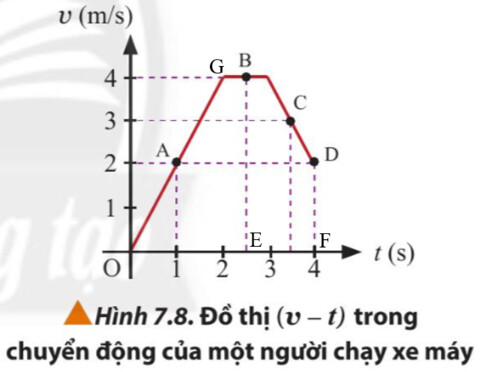
Từ A đến B, vật chuyển động nhanh dần đều
Từ B đến D, vật chuyển động thẳng đều
Từ D đến F, vật chuyển động chậm dần đều.
Giải SGK Luyện tập trang 44
a) Gia tốc của người này tại các thời điểm 1 s, 2,5 s và 3,5 s.
b) Độ dịch chuyển của người này từ khi bắt đầu chạy đến thời điểm 4 s.
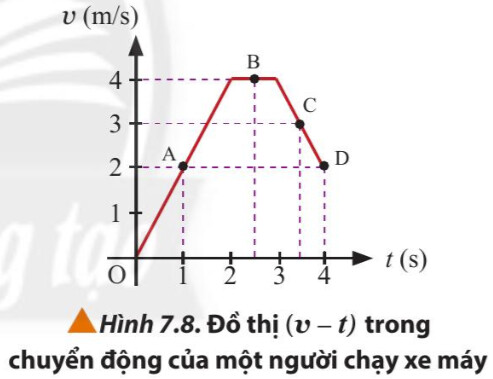
Biểu thức tính gia tốc: $a=\frac{v_2-v_1}{t_2-t_1}$
Độ dịch chuyển của vật trong khoảng thời gian từ t$_1$ đến t$_2$ được xác định bằng phần diện tích giới hạn bởi các đường v(t), v = 0, t = t$_1$, t = t$_2$ trong đồ thị (v – t).
a) Gia tốc của người này tại các thời điểm là:
+ t = 1 s: $a=\frac{v_2-v_1}{t_2-t_1} = \frac{2}{1} = 2 (m/s^2)$
+ t = 2,5 s: $a= 0 (m/s^2)$
+ t = 3,5 s: $a=\frac{v_2-v_1}{t_2-t_1} = \frac{3-4}{3,5-3} = -2 (m/s^2)$
b)
=> Độ dịch chuyển của người này là:
Giải SGK Mục 2 trang 44,45,46 Vật lí 10 Chân trời sáng tạo
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi hoạt động ở Mục 2 của các trang 44, 45,46 trong bài Gia tốc – Chuyển động thẳng biến đổi đều ở ngay bên dưới nhé!
Giải SGK Câu hỏi 6 trang 45
Phương trình liên hệ giữa gia tốc, vận tốc và độ dịch chuyển là:
$v^2-v_0^2=2 . a . d$
Trong đó:
+ $v$: vận tốc sau của vật (m/s)
+ $v_0$ : vận tốc ban đầu của vật (m/s)
+ $a$: gia tốc của vật (m/s$^2$ )
+ $d$: độ dịch chuyển (m).
Giải SGK Luyện tập trang 46
a) Tính gia tốc của tàu.
b) Tính quãng đường mà tàu đi được trong thời gian hãm phanh.
Biểu thức trong chuyển động biến đổi đều:
$v = v_0 + a.t$
$v^2 – v_0^2 = 2.a.d$
1 m/s = 3,6 km/h
a) Ta có: v$_0$ = 43,2 km/h = 12 m/s; v = 0 m/s; t = 1 phút = 60 s.
Gia tốc của tàu là:
$a=\frac{v-v_0}{t}=\frac{0-12}{60}=-0,2\left(\mathrm{~m} / \mathrm{s}^2\right)$
b) Quãng đường mà tàu đi được là:
$d=\frac{v^2-v_0^2}{2 . a}=\frac{0-12^2}{2 \cdot(-0,2)}=360(\mathrm{~m})$
Giải SGK Bài tập trang 47 Vật lí 10 Chân trời sáng tạo
Cùng HocThatGioi ôn lại các kiến thức vừa học bằng cách tìm ra đáp án chính xác nhất cho các câu hỏi bài tập ở Phần bài tập ở trang 47 trong bài Gia tốc – Chuyển động thẳng biến đổi đều ở ngay bên dưới nhé!
Giải SGK Bài 1 trang 47
Biểu thức tính gia tốc: $a = \frac {v_2 – v_1} {t_2 – t_1} $
Đổi 297 km/h = 82,5 m/s
Gia tốc trung bình của máy bay trong quá trình bay là:
$a=\frac{v_2-v_1}{t_2-t_1}=\frac{82,5}{30}=2,75\left(\mathrm{~m} / \mathrm{s}^2\right)$
Giải SGK Bài 2 trang 47

Hãy vẽ đồ thị vận tốc – thời gian và mô tả tính chất chuyển động của vận động viên này.
+ Độ dốc đi lên, vận tốc tăng dần theo thời gian, vật chuyển động nhanh dần đều
+ Độ dốc nằm ngang, vận tốc không thay đổi theo thời gian, vật chuyển động thẳng đều
+ Độ dốc đi xuống, vận tốc giảm dần theo thời gian, vật chuyển động chậm dần đều.
Đồ thị vận tốc – thời gian:
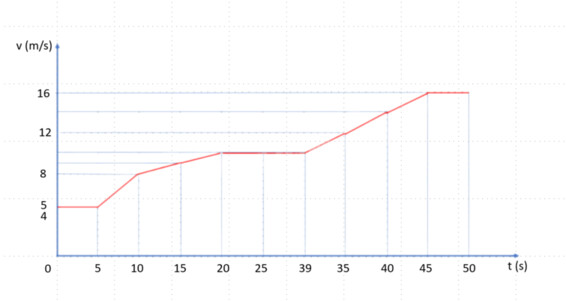
Mô tả chuyển động của vận động viên:
+ Từ 0 – 5 s đầu, vận động viên chuyển động thẳng đều
+ Từ 5 – 20 s tiếp theo, vận động viên chuyển động nhanh dần
+ Từ 20 – 30 s, vận động viên chuyển động thẳng đều
+ Từ 30 – 45 s, vận động viên chuyển động nhanh dần
+ Từ 45 – 50 s, vận động viên chuyển động thẳng đều.
Giải SGK Bài 3 trang 47
a) Hãy tính gia tốc của ô tô.
b) Xác định thời gian ô tô chạy thêm được 250 m kể từ khi bắt đầu hãm phanh.
c) Xe mất thời gan bao lâu để dừng hẳn kể từ lúc hãm phanh?
Biểu thức trong chuyển động biến đổi đều:
$v = v_0 + a.t$
$v^2 – v_0^2 = 2.a.d$
1 m/s = 3,6 km/h
Ta có v$_0$ = 54 km/h = 15 m/s; v = 5 m/s; d = 250 m
a) Gia tốc của ô tô là:
$a=\frac{v^2-v_0^2}{2 . d}=\frac{5^2-15^2}{2.250}=-0,4\left(\mathrm{~m} / \mathrm{s}^2\right)$
b) Thời gian ô tô chạy thêm được 250 m kể từ khi bắt đầu hãm phanh là:
$t=\frac{v-v_0}{a}=\frac{5-15}{-0,4}=25(s)$
c) Khi dừng hẳn thì v = 0 m/s
Thời gian kể từ lúc hãm phanh đến khi xe dừng hẳn là:
$t=\frac{v-v_0}{a}=\frac{0-15}{-0,4}=37,5(s)$
Giải SGK Bài 4 trang 47
a) Mô tả chuyển động của chất điểm.
b) Tính quãng đường mà chất điểm đi được từ khi bắt đầu chuyển động cho tới khi dừng lại.
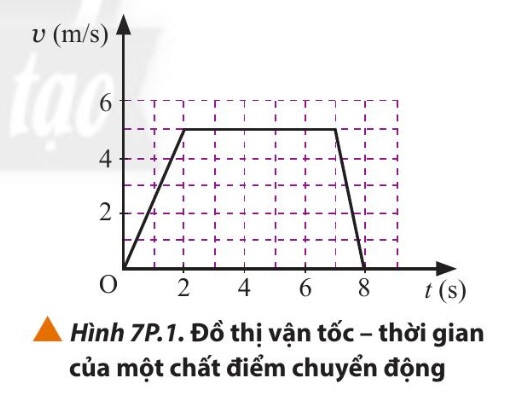
Quan sát hình
Biểu thức tính quãng đường trong chuyển động biến đổi đều
$a=\frac{v-v_0}{t} \Rightarrow s=\frac{v^2-v_0^2}{2 . a}$
Biểu thức tính quãng đường trong chuyển động thẳng đều:
$s= v . t$
a) Mô tả chuyển động của chất điểm:
+ Từ 0 – 2 s, vật chuyển động thẳng nhanh dần đều
+ Từ 2 – 7 s, vật chuyển động thẳng đều
+ Từ 7 – 8 s, vật chuyển động thẳng chậm dần đều
b) Quãng đường vật đi được trong 2 s đầu là:
$a_1=\frac{5-0}{2} = 2,5 (m/s^2) \Rightarrow s=\frac{5^2-0^2}{2 . 2}=6,25 (m)$
Quãng đường vật đi được từ 2 – 7 s là:
$s_2=5.(7−2)=25(m)$
Quãng đường vật đi được từ 7 – 8 s là:
$a_3=\frac{0-5}{8-7}=-5\left(m / s^2\right) \Rightarrow s_3=\frac{0^2-5^2}{2 \cdot(-5)}=2,5(m)$
=> Quãng đường mà chất điểm đi được từ lúc bắt đầu đến khi dừng hẳn là:
$S = 6,25 + 25 + 2,5 = 33,75 (m)$
Giải SGK Bài 5 trang 47
Biểu thức tính quãng đường trong chuyển động biến đổi đều:
$s=x_0+v_0 t+\frac{1}{2} a t^2$
Chọn gốc tọa độ và gốc thời gian là lúc xe bắt đầu xuất phát.
=> x$_0$ = 0; v$_0$ = 0
Gọi chiều dài 1 toa tàu là s
=> Chiều dài của 9 toa tàu là 9.s
Thời gian người nhìn thấy toa thứ nhất đi qua là 10 giây nên ta có:
$s=\frac{1}{2} . a . 10^2=50 . a$
=> Thời gian đi hết toa thứ 9 là:
$t=\sqrt{\frac{2 s_9}{a}}=\sqrt{\frac{2.9 . s}{a}}=\sqrt{\frac{2.9 .50 . a}{a}}=\sqrt{2.9 .50}=30(s)$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bài viết này đã giải quyết tất cả các bài tập, câu hỏi của Bài 7 Gia tốc – Chuyển động thẳng biến đổi đều thuộc Chương 3 Vật lí 10 Chân trời sáng tạo. Chúc các bạn học tốt và tiếp thu được nhiều kiến thức bổ ích nhé!





