Giải SGK bài Đường thẳng trong mặt phẳng tọa độ Toán 10 Chân trời sáng tạo
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Đường thẳng trong mặt phẳng tọa độ. Đây là bài học thuộc Bài 2 chương 9 sách Toán 10 Chân trời sáng tạo ở các trang 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi SGK bài Đường thẳng trong mặt phẳng tọa độ
Cùng HocThatGioi đi tìm đáp án cho các hoạt động khởi động, thực hành và vận dụng ở các trang 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57 trong bài Đường thẳng trong mặt phẳng tọa độ ở ngay bên dưới nhé!
Hoạt động khởi động trang 46
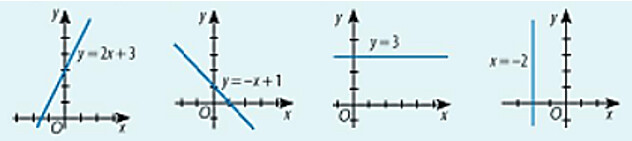
+) Hình 1: $y=2 x+3 \Rightarrow y-2 x-3=0$
Vậy $a=-1, b=1, c=-3$
+) Hình 2: $y=-x+1 \Rightarrow y+x-1=0$
Vậy $a=1, b=1, c=-1$
+) Hình 3: $y=3 \Rightarrow y-3=0$
Vậy $a=0, b=1, c=-3$
+ Hình 4: $x=-2 \Rightarrow x+2=0$
Vậy $a=1, b=0, c=2$
Hoạt động khám phá 1 trang 46
a) Tính tích vô hướng $\vec{n} \cdot \vec{u}$ và nêu nhận xét về phương của hai vectơ $\vec{n}, \vec{u}$.
b) Gọi $M(x ; y)$ là điểm di động trên $\Delta$. Chứng tỏ rằng vectơ $\overrightarrow{M_{0} M}$ luôn củng phương với vectơ $\vec{u}$ và luôn vuông góc với vectơ $\vec{n}$.
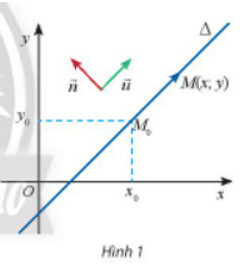
a)
+) Áp dụng ứng dụng biểu thức tọa độ của vectơ tính tích vô hướng
+) Dựa vào kết quả tích vô hướng các định phương (bằng 0 thì vuông góc)
b)
+) Xác định tỉ lệ giũa các tọa độ của hai vectơ để so sánh về phương
+) Tính tích vô hướng để chứng minh vuông góc
a) Ta có $\vec{n} \cdot \vec{u}=a \cdot b+b \cdot(-a)=0$
Tích vô hướng bằng 0 nên hai vectơ $\vec{n}, \vec{u}$ có phương vuông góc với nhau
b) Vectơ $\overrightarrow{M_0 M}$ có giá là đường thẳng $\Delta$
=> luôn cùng phương với vectơ $\vec{u}$
=> vectơ $\overrightarrow{M_0 M}$ có phương vuông góc với vectơ $\vec{n}$
Hoạt động khám phá 2 trang 47
M \text { và } M_0 \text { thuộc } \Delta \text { nên } \overrightarrow{M M}_0 \text { làm vectơ chỉ phương }
$\overrightarrow{M M}_0=\left(x_0-x ; y_0-y\right)$ mà $\Delta$ nhận $\overrightarrow{M M}_0$ làm vectơ chỉ phương nên ta có:
\left\{\begin{array} { l } { x _ { 0 } – x = u _ { 1 } } \\ { y _ { 0 } – y = u _ { 2 } } \end{array} \Rightarrow \left\{\begin{array}{l} x=x_0-u_1 \\ y=y_0-u_2 \end{array}\right.\right. \\ \text { Vậy } M\left(x_0-u_1 ; y_0-u_2\right)
Thực hành 1 trang 47
b) Tìm toạ độ điểm $P$ trên $\Delta$, biết $P$ có tung độ bằng 1 .
a) Phương trình tham số của đường thẳng $d:\left\{\begin{array}{l}x=-9+8 t \\ y=5-4 t\end{array}\right.$
b) Thay $y=1$ vào phương trình $y=5-4 t$ ta được $1=5-4 t \Rightarrow t=1$
Thay $t=1$ vào phương trình $x=-9+8 t$, ta được $x=-1$
Vậy $P(-1 ; 1)$
Vận dụng 1 trang 48
a) Viết phương trình tham số của đường thẳng $d$ biễu diễn đường đi của ô tô.
b) Tìm toạ độ của xe ứng với $t=2 ; t=4$.
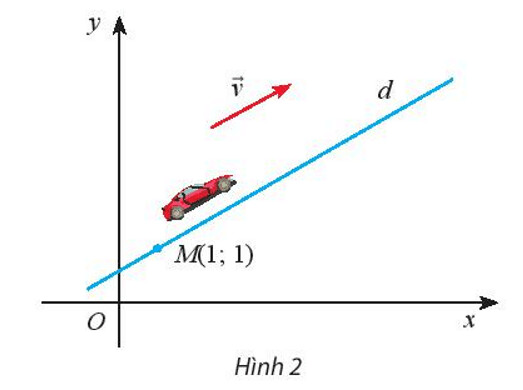
a) Phương trình tham số của đường thẳng $d:\left\{\begin{array}{l}x=1+40 t \\ y=1+30 t\end{array}\right.$
b) Thay $t=2$ vào phương trình d$:\left\{\begin{array}{l}x=1+40 t \\ y=1+30 t\end{array}\right.$ ta được $\left\{\begin{array}{l}x=1+40.2=81 \\ y=1+30.2=61\end{array}\right.$
Vậy khi $t=2$ thì tọa độ của ô tô là $(81 ; 61)$
Thay $t=4$ vào phương trìnhd $:\left\{\begin{array}{l}x=1+40 t \\ y=1+30 t\end{array}\right.$ ta được $\left\{\begin{array}{l}x=1+40.4=161 \\ y=1+30.4=121\end{array}\right.$
Vậy khi $t=4$ thì tọa độ của ô tô là $(161 ; 121)$
Hoạt động khám phá 3 trang 48
Bước 1: Tìm tọa độ điểm $M$ qua $M_0$ và $a, b$
Bước 2 : Thay vào phương trình
$\Delta$ nhận vectơ $\vec{n}=(a ; b)$ làm vectơ pháp tuyến, suy ra vectơ chỉ phương của $\Delta$ là $\vec{u}=(b ;-a)$
$M$ và $M_0$ thuộc đường thẳng $\Delta$ nên $\Delta$ nhận $\overrightarrow{M M}_0$ làm vectơ chỉ phương
\overrightarrow{M M}_0=\left(x_0-x ; y_0-y\right) \text {, suy ra } \\ \left\{\begin{array} { l } { x _ { 0 } – x = b } \\ { y _ { 0 } – y = – a } \end{array} \Rightarrow \left\{\begin{array}{l} x=x_0-b \\ y=y_0+a \end{array}\right.\right. \\ \text { Suy ra } M\left(x_0-u_1 ; y_0-u_2\right)
Thay tọa độ điểm $M$ vào phương trình $a x+b y+c=0$ ta có:
a\left(x_0-b\right)+b\left(y_0+a\right)+c=(-a b+b a)+\left(a x_0+b y_0+c\right) =0 \\ \left.\quad \text { (đúng vì }-a x_0-b y_0=c\right)
Vậy $M(x ; y)$ thỏa mãn phương trình đã cho
Thực hành 2 trang 49
a) Đường thẳng $\Delta$ đi qua điểm $A(1 ; 1)$ và có vectơ pháp tuyến $\vec{n}=(3 ; 5)$;
b) Đường thẳng $\Delta$ đi qua gốc toạ độ $O(0 ; 0)$ và có vectơ chỉ phương $\vec{u}=(2 ;-7)$;
c) Đường thẳng $\Delta$ đi qua hai điểm $M(4 ; 0), N(0 ; 3)$.
a) Đường thẳng $\Delta$ có vectơ pháp tuyến $\vec{n}=(3 ; 5)$ nên có vectơ chỉ phương $\vec{u}=(5 ;-3)$, nên ta có phương trình tham số của $\Delta$ là :
\left\{\begin{array}{l} x=1+5 t \\ y=1-3 t \end{array}\right.
Đường thẳng $\Delta$ đi qua điểm $A(1 ; 1)$ và có vectơ pháp tuyến $\vec{n}=(3 ; 5)$
Phương trình tổng quát của đường thẳng $d$ là: 3(x-1)+5(y-1)=0 \Leftrightarrow 3 x+5 y-8=0
b) Đường thẳng $\Delta$ đi qua gốc tọa độ $O(0 ; 0)$ và có vectơ chỉ phương $\vec{u}=(2 ;-7)$, nên có phương trình tham số là:
\left\{\begin{array}{l} x=2 t \\ y=-7 t \end{array}\right.
Đường thẳng $\Delta$ có vectơ chỉ phương $\vec{u}=(2 ;-7)$, nên có vectơ pháp tuyền là $\vec{n}=(7 ; 2)$ và đi qua $O(0 ; 0)$
Ta có phương trình tổng quát là:
7(x-0)+2(y-0)=0 \Leftrightarrow 7 x+2 y=0
c) Đường thẳng $\Delta$ đi qua hai điểm $M(4 ; 0), N(0 ; 3)$ nên có vectơ chỉ phương $\vec{u}=\overrightarrow{M N}=(-4 ; 3)$ và có vectơ pháp tuyến $\vec{n}=(3 ; 4)$
Phương trình tham số của $\Delta$ là: $\left\{\begin{array}{l}x=4-4 t \\ y=3 t\end{array}\right.$
Phương trình tổng quát của $\Delta$ là:
3(x-4)+4(x-0)=0 \Leftrightarrow 3 x+4 y-12=0
Vận dụng 2 trang 49
a) Viết phương trình tổng quát của đường thẳng $\Delta$ biểu diễn đường đi của điểm $M$.
b) Tìm toạ độ của điểm $M$ khi $\Delta$ cắt trục hoành.
a) Từ vectơ chỉ phương tìm vectơ pháp tuyến và viết phương trình tổng quát
VTCP $(a ; b)=>$ VTPT: $(-b ; a)$ hoặc $(b ;-a)$
b) $M$ thuộc trục hoành thì $M$ có tọa độ $(\mathrm{m} ; 0)$
a) Đường thẳng $\Delta$ có vectơ chỉ phương $\vec{v}=(3 ;-4)$,nên có vectơ pháp tuyền là $\vec{n}=(4 ; 3)$ và đi qua $A(1 ; 2)$
Ta có phương trình tổng quát là $4(x-1)+3(y-2)=0 \Leftrightarrow 4 x+3 y-10=0$
b) Điểm $M$ thuộc trục hoành nên tung độ bằng 0
Thay $y=0$ vào phương trình $4 x+3 y-10=0$ ta tìm được $x=\frac{5}{2}$
Vậy $\Delta$ cắt trục hoành tại điểm $M\left(\frac{5}{2} ; 0\right)$
Thực hành 3 trang 51
a) Ta có $3 x+5 y-8=0 \Leftrightarrow y=\frac{8}{5}-\frac{3}{5} x$
Vậy hàm số bậc ứng với đường thẳng $3 x+5 y-8=0$ là $y=\frac{8}{5}-\frac{3}{5} x$
b) Ta có $7 x+2 y=0 \Leftrightarrow y=-\frac{7}{2} x$
Vậy hàm số bậc ứng với đường thẳng $7 x+2 y=0$ là $y=-\frac{7}{2} x$
c) Ta có $3 x+4 y-12=0 \Leftrightarrow y=3-\frac{3}{4} x$
Vậy hàm số bậc ứng với đường thẳng $3 x+4 y-12=0$ là $y=3-\frac{3}{4} x$
Vận dụng 3 trang 51
a) Viết biểu thức tính thể tích $y$ của nước có trong bể sau $x$ giờ.
b) Gọi $y=f(x)$ là hàm số xác định được từ câu a). Vẽ đồ thị $d$ của hàm số này.
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng $d$.
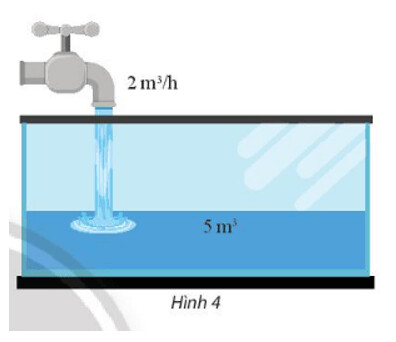
a) Thể tích nước trong bể được tính bằng công thức y=5+2x
b)
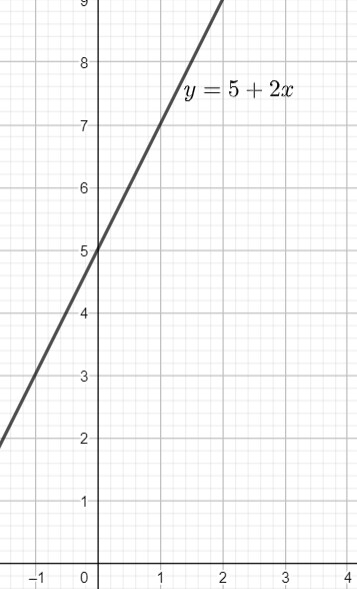
c) Ta có đồ thị hàm số bậc nhất $y=5+2 x \Leftrightarrow 2 x-y+5=0$
Vậy phương trình tổng quát của đường thẳng $d$ là $2 x-y+5=0$
Từ phương trình tổng quát ta có vectơ pháp tuyến $\vec{n}=(2 ;-1)$, từ đó ta có vectơ chỉ phương $\vec{u}=(1 ; 2)$
Khi $x=0$ thì $y=5$ nên đường thẳng đó đi qua điểm $(0 ; 5)$
Ta có phương trình tham số của đường thẳng d là $\left\{\begin{array}{l}x=t \\ y=5+2 t\end{array}\right.$
Hoạt động khám phá 4 trang 51
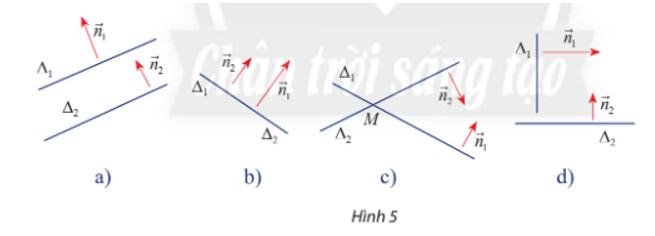
Nêu nhận xét về vị trí tương đối giữa $\Delta_{1}$ và $\Delta_{2}$ trong các trường hợp sau:
a) $\vec{n}_{1}$ và $\vec{n}_{2}$ cùng phương (Hình $5 \mathrm{a}, \mathrm{b}$ );
b) $\vec{n}_{1}$ và $\vec{n}_{2}$ không cùng phương (Hình $5 \mathrm{c}, \mathrm{d}$ );
c) $\vec{n}_{1}$ và $\vec{n}_{2}$ vuông góc (Hình $5 \mathrm{~d}$ ).
Dựa vào hình vẽ ta có
a) $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cùng phương thì hai đường thẳng $\Delta_1$ và $\Delta_2$ song song
b) $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ không cùng phương thì hai đường thẳng $\Delta_1$ và $\Delta_2$ cắt nhau
c) $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ vuông góc thì hai đường thẳng $\Delta_1$ và $\Delta_2$ vuông góc
Thực hành 4 trang 53
a) $d_{1}: x-5 y+9=0$ và $d_{2}: 10 x+2 y+7=10$,
b) $d_{1}: 3 x-4 y+9=0$ và $d_{2}:\left\{\begin{array}{l}x=1+4 t \\ y=1+3 t\end{array}\right.$
c) $d_{1}:\left\{\begin{array}{l}x=5+4 t \\ y=4+3 t\end{array}\right.$ và $d_{2}:\left\{\begin{array}{l}x=1+8 t \\ y=1+6 t\end{array}\right.$
Bước 1: Xác định cặp vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng
Bước 2:
+) Nếu 2 vecto cùng phương: Lấy điểm A thuộc d1. Kiểm tra A có thuộc d2 hay không.
=> KL: 2 đường thẳng song song nếu A không thuộc d2.
2 đường thẳng trùng nhau nếu A thuộc d2.
+) Nếu 2 vecto không cùng phương: Tính tích vô hướng
Nếu bằng 0 thì hai đường thẳng vuông góc, nếu khác 0 thì 2 đường thẳng chỉ cắt nhau.
=> Giải hệ phương trình từ hai đường thẳng để tìm giao điểm
a) $d_1$ và $d_2$ có vectơ pháp tuyến lần Iượt là $\overrightarrow{n_1}=(1 ;-5), \overrightarrow{n_2}=(10 ; 2)$
Ta có $\overrightarrow{n_1} \cdot \overrightarrow{n_2}=1.10+(-5) \cdot 2=0$ nên $\overrightarrow{n_1} \perp \overrightarrow{n_2}$
Giải hệ phương trình $\left\{\begin{array}{l}x-5 y+9=0 \\ 10 x+2 y+7=10\end{array}\right.$ ta được nghiệm $\left\{\begin{array}{l}x=-\frac{3}{52} \\ y=\frac{93}{52}\end{array}\right.$
Suy ra hai đường thẳng $d_1$ và $d_2$ vuông góc và cắt nhau tại $M\left(-\frac{3}{52} ; \frac{93}{52}\right)$
b) $d_1$ và $d_2$ có vectơ pháp tuyến lần lượt là
$\overrightarrow{n_1}=(3 ;-4), \overrightarrow{n_2}=(3,-4)$
$\overrightarrow{n_1}, \overrightarrow{n_2}$ trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra $d_1$ và $d_2$ song song hoặc trùng nhau
Lấy điểm $A(1 ; 1)$ thuộc $d_2$, thay tọa độ của $A$ vào phương trình $d_1$, ta được $3.1-4.1+9=8 \neq 0$, suy ra $A$ không thuộc đường thẳng $d_1$
Vậy hai đường thẳng $d_1$ và $d_2$ song song
c) $d_1$ và $d_2$ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}=(3 ;-4), \overrightarrow{n_2}=(6 ;-8)$
Ta có $a_1 b_2-a_2 b_1=3 \cdot(-8)-(-4) \cdot 6=0$ suy ra hai vectơ pháp tuyến cùng phương. Suy ra $d_1$ và $d_2$ song song hoặc trùng nhau
Lấy điểm $A(1 ; 1)$ thuộc $d_2$, thay tọa độ của $A$ vào phương trình $d_1$, ta được $\left\{\begin{array}{l}1=5+4 t \\ 1=4+3 t\end{array} \Leftrightarrow t=-1\right.$, suy ra $A$ thuộc đường thẳng $d_1$
Vậy hai đường thẳng $d_1$ và $d_2$ trùng nhau
Vận dụng 4 trang 53
a) Đi qua điểm $A(2 ; 3)$ và song song với đường thẳng $d_{2}: x+3 y+2=0$;
b) Đi qua điểm $B(4 ;-1)$ và vuông góc với đường thẳng $d_{3}: 3 x-y+1=0$.
Bước 1: Từ đường thẳng đã cho xác định vectơ pháp tuyến hoặc vectơ chỉ phương
Bước 2: Viết phương trình tổng quát hoặc phương trình tham số
a) $d_1$ song song với đường thẳng $d_2: x+3 y+2=0$ nên nhận vectơ pháp tuyến của đường thẳng $d_2$ làm vectơ pháp tuyến là $\vec{n}=(1 ; 3)$
$d_1$ đi qua điểm $A(2 ; 3)$ nên ta có phương trình tổng quát
(x-2)+3 \cdot(y-3)=0 \Leftrightarrow x+3 y-11=0
b) $d_1$ vuông góc với đường thẳng $d_3: 3 x-y+1=0$ nên nhận vectơ pháp tuyến của đường thẳng $d_3$ làm vectơ chỉ phương là $\vec{u}=(3 ;-1)$
$d_1$ đi qua điểm $B(4 ;-1)$ nên ta có phương trình tham số:
\left\{\begin{array}{l} x=4+3 t \\ y=-1-t \end{array}\right.
Hoạt động khám phá 5 trang 54
Tính số đo các góc $\widehat{x O t}, \widehat{t O y}$ và $\widehat{y O z}$.
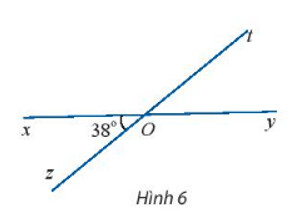
Ta có hai góc $\widehat{x O z}$ và $\widehat{t O y}$ đối đỉnh nên $\widehat{x O z}=\widehat{t O y}=38^{\circ}$ hai góc $\widehat{x O t}$ và $\widehat{y O z}$ đối đỉnh nên $\widehat{x O t}=\widehat{y O z}$
$\widehat{x O z}$ và $\widehat{x O t}$ bù nhau nên $\widehat{x O t}=180^{\circ}-\widehat{x O z}=180^{\circ}-38^{\circ}=142^{\circ}$
Vậy $\widehat{x O z}=\widehat{t O y}=38^{\circ}$ và $\widehat{x O t}=\widehat{y O z}=142^{\circ}$
Hoạt động khám phá 6 trang 54
\Delta_{1}: a_{1} x+b_{1} y+c_{1}=0\left(a_{1}^{2}+b_{1}^{2}>0\right) \text { và } \Delta_{2}: a_{2} x+b_{2} y+c_{2}=0\left(a_{2}^{2}+b_{2}^{2}>0\right)
có vectơ pháp tuyến lần lượt là $\vec{n}_{1}$ và $\vec{n}_{2}$.
Tìm toạ độ của $\vec{n}_{1}, \vec{n}_{2}$ và tính $\cos \left(\vec{n}_{1}, \vec{n}_{2}\right)$.
+) Tọa độ của $\overrightarrow{n_1}, \overrightarrow{n_2}$ được xác định từ phương trình tổng quát của hai đường thẳng
+) Áp dụng biểu thức tọa độ của vectơ trong mặt phẳng
+) Từ phương trình $\Delta_1: a_1 x+b_1 y+c_1=0$ ta xác định được tọa độ của vectơ $\overrightarrow{n_1}$ là $\left(a_1 ; b_1\right)$
+) Từ phương trình $\Delta_2: a_2 x+b_2 y+c_2=0$ ta xác định được tọa độ của vectơ $\overrightarrow{n_2}$ là $\left(a_2 ; b_2\right)$
\text { +) } \cos \left(\overrightarrow{n_1}, \overrightarrow{n_2}\right)=\frac{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right| \cdot \overrightarrow{\vec{n}_2} \mid}=\frac{a_1 a_2+b_1 b_2}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2{ }^2}}
Thực hành 5 trang 56
a) $\Delta_{1}: x+3 y-7=0$
và $\Delta_{2}: x-2 y+3=0$
b) $\Delta_{1}: 4 x-2 y+5=0$
và $\Delta_{2}:\left\{\begin{array}{l}x=t \\ y=13+2 t\end{array}\right.$
c) $\Delta_{1}:\left\{\begin{array}{l}x=1+t \\ y=3+2 t\end{array}\right.$
và $\Delta_{2}:\left\{\begin{array}{l}x=-7+2 t \\ y=1-t .\end{array}\right.$
Bước 1: Xác định vectơ pháp tuyến của hai đường thẳng đã cho
Bước 2: Tính số đo góc giữa hai đường thẳng bằng công thức
\cos \left(\Delta_1, \Delta_2\right)=\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1{ }^2+b_1{ }^2} \sqrt{a_2{ }^2+b_2{ }^2}}
a) Ta có vectơ pháp tuyến của hai đường thẳng $\Delta_1$ và $\Delta_2$ lần lượt là $\overrightarrow{n_1}=(1 ; 3), \overrightarrow{n_2}=(1 ;-2)$
Ta có $\cos \left(\Delta_1, \Delta_2\right)=\frac{|1.1+3 .(-2)|}{\sqrt{1^2+3^2} \sqrt{1^2+(-2)^2}} \approx 0,93 \Rightarrow\left(\Delta_1, \Delta_2\right) \approx 22^{\circ} 8^{\prime}$
b) Ta có vectơ pháp tuyến của hai đường thẳng $\Delta_1$ và $\Delta_2$ lần lượt là $\overrightarrow{n_1}=(4 ;-2), \overrightarrow{n_2}=(2 ;-1)$
Ta có $\cos \left(\Delta_1, \Delta_2\right)=\frac{|4 \cdot 2+(-2) \cdot(-1)|}{\sqrt{4^2+(-2)^2} \sqrt{2^2+(-1)^2}}=1 \Rightarrow\left(\Delta_1, \Delta_2\right)=0^{\circ}$
c) Ta có vectơ pháp tuyến của hai đường thẳng $\Delta_1$ và $\Delta_2$ lần lượt là $\overrightarrow{n_1}=(2 ;-1), \overrightarrow{n_2}=(1 ; 2)$
Ta có $a_1 a_2+b_1 b_2=2.1+(-1) \cdot 2=0$
Suy ra $\left(\Delta_1, \Delta_2\right)=90^{\circ}$
Vận dụng 5 trang 56
Bước 1: Viết phương trình tổng quat từ đồ thị của hai hàm số đã cho
Bước 2: Xác định vectơ pháp tuyền
Bước 3: \cos \left(\Delta_1, \Delta_2\right)=\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1{ }^2+b_1{ }^2} \sqrt{a_2{ }^2+b_2{ }^2}}
Từ đồ thị hàm số ta có phương trình tổng quát
y=x \Leftrightarrow d_1: x-y=0, y=2 x+1 \Leftrightarrow 2 x-y+1=0
Từ đó ta có vectơ pháp tuyến lần lượt là
\overrightarrow{n_1}=(1 ;-1), \overrightarrow{n_2}=(2 ;-1) \\ \cos \left(d_1, d_2\right)=\frac{|1.2+(-1) \cdot(-1)|}{\sqrt{1^2+(-1)^2} \sqrt{2^2+(-1)^2}}=\frac{3 \sqrt{10}}{10} \Rightarrow\left(d_1, d_2\right) \approx 18^{\circ} 26^{\prime}
Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng $18^{\circ} 26^{\prime}$
Hoạt động khám phá 7
a) Chứng minh rằng hai vectơ $\vec{n}$ và $\overrightarrow{H M_{0}}$ cùng phương và tìm toạ độ của chúng.
b) Gọi $p$ là tích vô hướng của hai vectơ $\vec{n}$ và $\overrightarrow{H M_{0}}$. Chứng minh rằng $p=a x_{0}+b y_{0}+c$.
c) Giải thích công thức $\left|\overrightarrow{H M_{0}}\right|=\frac{|p|}{|\vec{n}|}$.
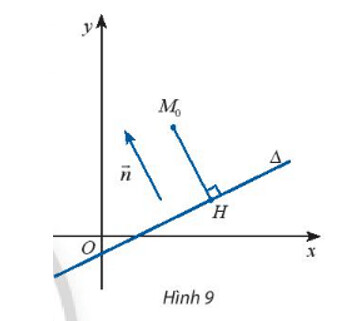
a) So sánh phương với vectơ chỉ phương
b)
Bước 1: Nhân tích vô hướng của hai vectơ
Bước 2: Thay tọa độ điẻm H vào đường thẳng tìm mối liên hệ
c) Thay vào công thức kết quả đã tìm được ở câu b)
a) Ta có: $\vec{n}$ và $\overrightarrow{H M_0}=\left(x_0-x_H ; y_0-y_H\right)$
Mà $H$ là hình chiếu vuông góc của $M_0$ trên $\Delta$ nên $H M_0 \perp \Delta$
Mặt khác vectơ pháp tuyến $\vec{n}$ cùng vuông góc với $\Delta$
Suy ra $\vec{n}$ và $\overrightarrow{H M_0}$ cùng phương (đpcm)
b) Ta có: $\vec{n}=(a ; b)$ và $\overrightarrow{H M_0}=\left(x_0-x_H ; y_0-y_H\right)$
Suy ra
p=\vec{n} \cdot \overrightarrow{H M_0}=a\left(x_0-x_H\right)+b\left(y_0-y_H\right)=a x_0+b y_0 \\ -\left(a x_H+b y_H\right)(1)
Mà $H$ thuộc đường thẳng $\Delta$ nên tọa độ điểm $H$ thỏa mãn phương trình đường thẳng $\Delta$
Thay tọa độ điểm $H$ vào phương trình $\Delta: a x+b y+c=0\left(a^2+b^2>0\right)$ ta có: $a x_H+b y_H+c=0 \Leftrightarrow c=-\left(a x_H+b y_H\right)$
Thay $c=-\left(a x_H+b y_H\right)$ vào (1) ta có $p=a x_0+b y_0+c \quad$ (đpcm)
c) Ta có:
p=\vec{n} \cdot \overrightarrow{H M_0} \Leftrightarrow \overrightarrow{H M_0}=\frac{p}{\vec{n}} \Rightarrow\left|\overrightarrow{H M_0}\right|=\left|\frac{p}{\vec{n}}\right| \Rightarrow\left|\overrightarrow{H M_0}\right|=\frac{|p|}{|\vec{n}|}
Thực hành 6 trang 57
Bước 1: Viết phương trình tổng quat của các đường thẳng $A B, A C$, $B C$
Bước 2: Đường của kẻ từ $A$ chính là khoảng cách từ điểm $A$ đến đường thẳng $B C$ (tương tự các đường cao còn lại)
Ta có: $\overrightarrow{A B}=(4 ; 1), \overrightarrow{A C}=(3 ; 3), \overrightarrow{B C}=(-1 ; 2)$
+) Đường thẳng $A B$ nhận vectơ $\overrightarrow{A B}=(4 ; 1)$ làm phương trình chỉ phương nên có vectơ pháp tuyến là $\overrightarrow{n_1}=(1 ;-4)$ và đi qua điểm $A(1 ; 1)$, suy ra ta có phương trình tổng quát của đường thẳng $A B$ là:
(x-1)-4(y-1)=0 \Leftrightarrow x-4 y+3=0
Độ dài đường cao kẻ từ $C$ chính là khoảng cách từ điểm $C$ đến đường thẳng $A B$
d(C, A B)=\frac{|4-4.4+3|}{\sqrt{1^2+4^2}}=\frac{9 \sqrt{17}}{17}
+) Đường thẳng $B C$ nhận vectơ $\overrightarrow{B C}=(-1 ; 2)$ làm phương trình chỉ phương nên có vectơ pháp tuyến là $\overrightarrow{n_2}=(2 ; 1)$ và đi qua điểm $B(5 ; 2)$, suy ra ta có phương trình tổng quát của đường thẳng $\mathrm{BC}$ là: $2(x-5)+(y-2)=0 \Leftrightarrow 2 x+y-12=0$
Độ dài đường cao kẻ từ $A$ chính là khoảng cách từ điểm $A$ đến đường thẳng $B C$
d(A, B C)=\frac{|2.1+1-12|}{\sqrt{2^2+1^2}}=\frac{9 \sqrt{5}}{5}
+) Đường thẳng $A C$ nhận vectơ $\overrightarrow{A C}=(3 ; 3)$ làm phương trình chỉ phương nên có vectơ pháp tuyến là $\overrightarrow{n_3}=(1 ;-1)$ và đi qua điểm $A(1 ; 1)$, suy ra ta có phương trình tổng quát của đường thẳng $A C$ là:
(x-1)-(y-1)=0 \Leftrightarrow x-y=0
Độ dài đường cao kẻ từ $B$ chính là khoảng cách từ điểm $B$ đến đường thẳng $A C$
d(B, A C)=\frac{|5-2|}{\sqrt{1^2+1^2}}=\frac{3 \sqrt{2}}{2}
Vận dụng 6 trang 57
Khoảng cách giữa hai đường thẳng song song là khoảng cách một điềm bất kì từ đường thẳng này tới đường thẳng còn lại
Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm $A(0 ; 4) \in d_2$, suy ra $d\left(d_1, d_2\right)=d\left(A, d_1\right)=\frac{|4.0-3.4+2|}{\sqrt{4^2+3^2}}=2$
Vậy khoảng cách giữa hai đường thẳng $d_1: 4 x-3 y+2=0$ và $d_2: 4 x-3 y+12=0$ là 2
Giải bài tập SGK trang 57, 58 bài Đường thẳng trong mặt phẳng tọa độ
Những bài tập SGK ở cuối bài Đường thẳng trong mặt phẳng tọa độ trang 56, 57 sách Toán 10 Chân trời sáng tạo sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 1 trang 57
a) $d$ đi qua điểm $A(-1 ; 5)$ và có vectơ chỉ phương $\vec{u}=(2 ; 1)$;
b) $d$ đi qua điểm $B(4 ;-2)$ và có vectơ pháp tuyến là $\vec{n}=(3 ;-2)$;
c) $d$ đi qua $P(1 ; 1)$ và có hệ số góc $k=-2$;
d) $d$ đi qua hai điểm $Q(3 ; 0)$ và $R(0 ; 2)$.
a) Đường thẳng $d$ đi qua điểm $A(-1 ; 5)$ và có vectơ chỉ phương $\vec{u}=(2 ; 1)$, nên có phương trình tham số là:
\left\{\begin{array}{l} x=-1+2 t \\ y=5+t \end{array}\right.
Đường thẳng $d$ có vectơ chỉ phương $\vec{u}=(2 ; 1)$, nên có vectơ pháp tuyền là $\vec{n}=(1 ;-2)$ và đi qua $A(-1 ; 5)$
Ta có phương trình tổng quát là
(x+1)-2(y-5)=0 \Leftrightarrow x-2 y+11=0
b) Đường thẳng $d$ có vectơ pháp tuyến $\vec{n}=(3 ;-2)$ nên có vectơ chỉ phương $\vec{u}=(2 ; 3)$, và đi qua điểm $B(4 ;-2)$ nên ta có phương trình tham số của $d$ là :
\left\{\begin{array}{l} x=4+2 t \\ y=-2+3 t \end{array}\right.
Đường thẳng $d$ đi qua điểm $B(4 ;-2)$ và có vectơ pháp tuyến $\vec{n}=(3 ;-2)$
Phương trình tổng quát của đường thẳng $d$ là:
3(x-4)-2(y+2)=0 \Leftrightarrow 3 x-2 y-16=0
c) Đường thẳng $d$ có dạng $y=a x+b$
$d$ đi qua $P(1 ; 1)$ và có hệ số góc $k=-2$ nên ta có:
$1=-2.1+b \Rightarrow b=3$
Suy ra đồ thị đường thẳng $d$ có dạng $y=-2 x+3$
Vậy đường thẳng $d$ có phương trình tổng quát là $y+2 x-3=0$
Suy ra đường thẳng $d$ có vectơ pháp tuyến $\vec{n}=(2 ; 1)$, nên có vectơ chỉ phương là $\vec{u}=(1 ;-2)$ và đi qua điểm $P(1 ; 1)$ nên ta có phương trình tham số của $d$ là :
\left\{\begin{array}{l} x=1+t \\ y=1-2 t \end{array}\right.
d) Đường thằng $d$ đi qua hai điểm $Q(3 ; 0)$ và $R(0 ; 2)$ nên có vectơ chỉ phương $\vec{u}=\overrightarrow{Q R}=(-3 ; 2)$ và có vectơ pháp tuyến $\vec{n}=(2 ; 3)$
Phương trình tham số của $\Delta$ là: $\left\{\begin{array}{l}x=3-3 t \\ y=2 t\end{array}\right.$
Phương trình tổng quát của $\Delta$ là:
2(x-3)+3(x-0)=\Leftrightarrow 2 x+3 y-6=0
Bài 2 trang 57
a) Lập phương trình tổng quát của đường thẳng $B C$.
b) Lập phương trình tham số của trung tuyến $A M$.
c) Lập phương trình của đường cao $A H$.
a) Ta có: $\overrightarrow{B C}=(4 ; 2) \Rightarrow V T P T: \overrightarrow{n_{B C}}=(2 ;-4)$
Phương trình tổng quát của đường thẳng $B C$ đi qua điểm $B(1 ; 2)$ và nhận vectơ $\vec{n}=(2 ;-4)$ làm VTPT là:
2(x-1)-4(y-2)=0 \Leftrightarrow 2 x-4 y+6=0
b) $M$ là trung điểm của $B C$ nên ta có tọa độ điểm $M$ là $M(3 ; 3)$
Đường thẳng $A M$ đi qua điểm $A(2 ; 5)$ và nhận vectơ $\overrightarrow{A M}=(1 ;-2)$ làm vectơ chỉ phương nên ta có phương trình tham số của trung tuyến $A M$ là:
\left\{\begin{array}{l} x=2+t \\ y=5-2 t \end{array}\right.
c) Ta có: $A H \perp B C$ nên đường cao $A H$ nhận vectơ $\overrightarrow{B C}=(4 ; 2)$ làm vectơ pháp tuyến
Đường thẳng $A H$ đi qua $A(2 ; 5)$ và nhận vectơ $\overrightarrow{B C}=(4 ; 2)$ làm vectơ pháp tuyến, suy ta phương trình tổng quát của đường cao $A H$ là:
4(x-2)+2(y-5)=0 \Leftrightarrow 4 x+2 y-18=0
Bài 3 trang 57
a) $\triangle$ đi qua $A(2 ; 1)$ và song song với đường thẳng $3 x+y+9=0$;
b) $\Delta$ đi qua $B(-1 ; 4)$ và vuông góc với đường thẳng $2 x-y-2=0$.
Bước 1: Từ đường thẳng đã cho xác định vectơ pháp tuyến hoặc vectơ chỉ phương
Bước 2: Viết phương trình tổng quát và phương trình tham số
a) $\Delta$ song song với đường thẳng $3 x+y+9=0$ nên nhận vectơ pháp tuyến của đường thẳng này làm vectơ pháp tuyến là $\vec{n}=(3 ; 1)$
$\Delta$ đi qua điểm $A(2 ; 1)$ nên ta có phương trình tổng quát
3(x-2)+(y-1)=0 \Leftrightarrow 3 x+y-7=0
$\Delta$ có vectơ pháp tuyến $\vec{n}=(3 ; 1)$ nên có vectơ chỉ phương là $\vec{u}=(1 ;-3)$
Phương trình tham số của đường thẳng $\Delta$ là:
\left\{\begin{array}{l} x=2+t \\ y=1-3 t \end{array}\right.
b) $\Delta$ vuông góc với đường thẳng $2 x-y-2=0$ nên nhận vectơ pháp tuyến của đường thẳng này làm vectơ chỉ phương là $\vec{u}=(2 ;-1)$
$\Delta$ đi qua điểm $B(-1 ; 4)$ nên ta có phương trình tham số: $\left\{\begin{array}{l}x=-1+2 t \\ y=4-t\end{array}\right.$
$\Delta$ có vectơ chỉ phương $\vec{u}=(2 ;-1)$ nên có vectơ pháp tuyến là $\vec{n}=(1 ; 2)$
Phương trình tổng quát của đường thẳng $\Delta$ là:
(x+1)+2(y-4)=0 \Leftrightarrow x+2 y-7=0
Bài 4 trang 57
a) $d_{1}: x-y+2=0$ và $d_{2}: x+y+4=0$,
b) $d_{1}:\left\{\begin{array}{l}x=1+2 t \\ y=3+5 t\end{array}\right.$ và $d_{2}: 5 x-2 y+9=0$,
c) $d_{1}:\left\{\begin{array}{l}x=2-t \\ y=5+3 t\end{array}\right.$ và $d_{2}: 3 x+y-11=0$.
Bước 1: Xác định cặp vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng: $\left(a_1 ; b_1\right)$ và $\left(\mathrm{a}_2 ; \mathrm{b}_2\right)$
Bước 2:
+) Nếu 2 vecto cùng phương: Lấy điểm $A$ thuộc d1. Kiểm tra A có thuộc $\mathrm{d} 2$ hay không.
=> KL: 2 đường thẳng song song nếu $\mathrm{A}$ không thuộc $\mathrm{d} 2$.
2 đường thẳng trùng nhau nếu $A$ thuộc $\mathrm{d} 2$.
+) Nếu 2 vecto không cùng phương: Tính tích vô hướng
Nếu bằng 0 thì hai đường thẳng vuông góc, nếu khác 0 thì 2 đường thẳng chỉ cắt nhau.
=> Giải hệ phương trình từ hai đường thẳng để tìm giao điểm
a) $d_1$ và $d_2$ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}=(1 ;-1), \overrightarrow{n_2}=(1 ; 1)$
Ta có $\overrightarrow{n_1} .\overrightarrow{n_2}=1.1+(-1) .1=0$ nên $\overrightarrow{n_1} \perp \overrightarrow{n_2}$
Giải hệ phương trình $\left\{\begin{array}{l}x-y+2=0 \\ x+y+4=0\end{array}\right.$ ta được nghiệm $\left\{\begin{array}{l}x=-3 \\ y=-1\end{array}\right.$
Suy ra hai đường thẳng $d_1$ và $d_2$ vuông góc và cắt nhau tại $M(-3 ;-1)$
b) $d_1$ và $d_2$ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}=(5 ;-2), \overrightarrow{n_2}=(5 ;-2)$
$\overrightarrow{n_1}, \overrightarrow{n_2}$ trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra $d_1$ và $d_2$ song song hoặc trùng nhau
Lấy điểm $A(1 ; 3)$ thuộc $d_1$, thay tọa độ của $A$ vào phương trình $d_2$, ta được $5.1-2.3+9=8 \neq 0$, suy ra $A$ không thuộc đường thẳng $d_2$
Vậy hai đường thẳng $d_1$ và $d_2$ song song
c) $d_1$ và $d_2$ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}=(3 ; 1), \overrightarrow{n_2}=(3 ; 1)$
Suy ra hai vectơ pháp tuyến cùng phương. Suy ra $d_1$ và $d_2$ song song hoặc trùng nhau
Lấy điểm $A(2 ; 5)$ thuộc $d_1$, thay tọa độ của $A$ vào phương trình $d_2$, ta được $3.2+5-11=0$, suy ra $A$ thuộc đường thẳng $d_2$
Vậy hai đường thẳng $d_1$ và $d_2$ trùng nhau
Bài 5 trang 58
Tìm giao điểm của $d$ với hai trục toạ độ.
+) A là giao của d với $O x=>A(a ; 0)$ thuộc $d$.
+) A là giao của d với $O y=>A\left(0 ; a^{\prime}\right)$ thuộc $d$.
+) Gọi $A$ là giao điểm của đường thẳng $d$ với trục tung
Suy ra tọa độ của $A$ là: $A(0 ; y)$
Thay $x=0$ vào phương trình $\left\{\begin{array}{l}x=2-t \\ y=5+3 t\end{array}\right.$ ta có:
\left\{\begin{array} { l } { 0 = 2 – t } \\ { y = 5 + 3 t } \end{array} \Leftrightarrow \left\{\begin{array}{l} t=2 \\ y=11 \end{array}\right.\right.
Vậy giao điểm của $d$ với trục tung là $A(0 ; 11)$
+) Gọi $B$ là giao điểm của đường thẳng $d$ với trục hoành
Suy ra tọa độ của $B$ là: $B(x ; 0)$
Thay $y=0$ vào phương trình $\left\{\begin{array}{l}x=2-t \\ y=5+3 t\end{array}\right.$ ta có:
\left\{\begin{array} { l } { x = 2 – t } \\ { 0 = 5 + 3 t } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=\frac{11}{3} \\ t=-\frac{5}{3} \end{array}\right.\right.
Vậy giao điểm của $d$ với trục hoành là $B\left(\frac{11}{3} ; 0\right)$
Bài 6 trang 58
a) $d_{1}: x-2 y+3=0 \quad$ và $d_{2}: 3 x-y-11=0$;
b) $d_{1}:\left\{\begin{array}{l}x=t \\ y=3+5 t\end{array} \quad\right.$ và $d_{2}: x+5 y-5=0$,
c) $d_{1}:\left\{\begin{array}{l}x=3+2 t \\ y=7+4 t\end{array} \quad\right.$ và $\quad d_{2}:\left\{\begin{array}{l}x=t \\ y=-9+2 t \text {. }\end{array}\right.$
Bước 1: Xác định 2 vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng đã cho: $\left(a_1 ; b_1\right),\left(a_2 ; b_2\right)$
Bước 2: Tính cos góc giữa hai đường thẳng bằng công thức $\cos \left(d_1, d_2\right)=\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}=>$ suy ra góc giữa 2 đt.
a) Ta có vectơ pháp tuyến của hai đường thẳng $d_1$ và $d_2$ lần lượt là $\overrightarrow{n_1}=(1 ;-2), \overrightarrow{n_2}=(3 ;-1)$
Ta có $\cos \left(d_1, d_2\right)=\frac{|1 \cdot 3+(-2) \cdot(-1)|}{\sqrt{1^2+(-2)^2} \sqrt{3^2+(-1)^2}}=\frac{\sqrt{2}}{2} \Rightarrow\left(d_1, d_2\right)$ $=45^{\circ}$
b) Ta có vectơ pháp tuyến của hai đường thẳng $d_1$ và $d_2$ lần lượt là $\overrightarrow{n_1}=(5 ;-1), \overrightarrow{n_2}=(1 ; 5)$
Ta có $a_1 a_2+b_1 b_2=5.1+(-1) .5=0$
Suy ra $\left(d_1, d_2\right)=90^{\circ}$
c) Ta có vectơ chỉ phương của hai đường thẳng $\Delta_1$ và $\Delta_2$ lần lượt là $\overrightarrow{u_1}=(2 ; 4), \overrightarrow{u_2}=(1 ; 2)$
\cos \left(d_1, d_2\right)=\frac{|2.1+4.2|}{\sqrt{2^2+4^2} \sqrt{1^2+2^2}}=1 \Rightarrow\left(d_1, d_2\right)=0^{\circ}
Bài 7 trang 58
a) $M(1 ; 2)$ và $\Delta: 3 x-4 y+12=0$;
b) $M(4 ; 4)$ và $\Delta:\left\{\begin{array}{l}x=t \\ y=-t\end{array}\right.$
c) $M(0 ; 5)$ và $\Delta:\left\{\begin{array}{l}x=t \\ y=\frac{-19}{4}\end{array}\right.$
d) $M(0 ; 0)$ và $\Delta: 3 x+4 y-25=0$.
Bước 1: Xác định phương trình tổng quát của $\Delta: a x_0+b y_0+c=0$
Bước 2: khoảng cách từ $A\left(x_0 ; y_0\right)$ đến d là: $d(A, \Delta)=\frac{\left|a x_0+b y_0+c\right|}{\sqrt{a^2+b^2}}$
a) Khoảng cách từ $M(1 ; 2)$ đến $\Delta: 3 x-4 y+12=0$ là:
d(M, \Delta)=\frac{|3.1-4.2+12|}{\sqrt{3^2+4^2}}=\frac{7}{5}
b) $\Delta$ có phương trình tham số $\Delta:\left\{\begin{array}{l}x=t \\ y=-t\end{array}\right.$ nên có phương trình tổng quát là
(x-0)+(y-0)=0 \Leftrightarrow x+y=0
Suy ra khoảng cách từ điểm $M(4 ; 4)$ đến đường thẳng $\Delta$ là
d(M, \Delta)=\frac{|1.4+1.4|}{\sqrt{1^2+1^2}}=2 \sqrt{2}
c) $\Delta$ có phương trình tham số $\Delta:\left\{\begin{array}{l}x=t \\ y=\frac{-19}{4}\end{array}\right.$ nên có phương trình tổng quát là
$0 .(x-0)+\left(y+\frac{19}{4}\right)=0 \Leftrightarrow y+\frac{19}{4}=0$
Suy ra khoảng cách từ điểm $M(0 ; 5)$ đến đường thẳng $\Delta$ là
d(M, \Delta)=\frac{\left|5+\frac{19}{4}\right|}{\sqrt{0^2+1^2}}=\frac{39}{4}
d) Khoảng cách từ $M(0 ; 0)$ đến $\Delta: 3 x+4 y-25=0$ là:
d(M, \Delta)=\frac{|3.0+4.0-25|}{\sqrt{3^2+4^2}}=5
Bài 8 trang 58
+) Khoảng cách giữa hai đường thẳng song song là khoảng cách một điểm bất kì từ đường thẳng này tới đường thẳng còn lại
+) khoảng cách từ $A\left(x_0 ; y_0\right)$ đến d là:
d(A, \Delta)=\frac{\left|a x_0+b y_0+c\right|}{\sqrt{a^2+b^2}}
Ta có vectơ pháp tuyến của hai đường thẳng là $\overrightarrow{n_1}=(3 ; 4), \overrightarrow{n_2}=(6 ; 8)$ suy ra hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm $A\left(0 ; \frac{5}{2}\right) \in \Delta$, suy ra
d\left(\Delta, \Delta^{\prime}\right)=d\left(A, \Delta^{\prime}\right)=\frac{\left|6.0+8 \cdot \frac{5}{2}-1\right|}{\sqrt{6^2+8^2}}=\frac{19}{10}
Vậy khoảng cách giữa hai đường thẳng
$\Delta: 3 x+4 y-10=0$ và $\Delta^{\prime}: 6 x+8 y-1=0$ là $\frac{19}{10}$
Bài 9 trang 58
Khi M nằm trên đường thẳng d thì khoảng ngắn nhất là đoạn vuông góc
Điểm $S$ nằm trên đường thẳng $d$, nên khi $S$ di động trên đoạn thẳng $d$ thì $S M$ ngắn nhất khi $S M \perp d$
Nên khoảng cách ngắn nhất từ điểm $M(5 ; 10)$ đến điểm $S$ là khoảng cách từ điểm $M(5 ; 10)$ đến d Khoảng cách đó là: $d(M, d)=\frac{|12.5-5.10+16|}{\sqrt{12^2+5^2}}=2$
Vậy khi $S$ di động trên đường thẳng $d$ thì khoảng cách ngắn nhất từ điểm $M(5 ; 10)$ đến điểm $S$ là 2.
Bài 10 trang 58
a) Viết phương trình các đường thẳng $A B, A C, B C$.
b) Tính góc hợp bởi hai đường thẳng $A B$ và $A C$.
c) Tính khoảng cách từ điểm $A$ đến đường thẳng $B C$.
a) Tìm VTPT (hoặc VTCP) => Lập PT tổng quát (hoặc tham số) của đt.
b) Xác định góc giữa hai đường thẳng thông qua cặp VTPT ( hoặc VTCP): $\left(a_1 ; b_1\right),\left(a_2 ; b_2\right)$
\cos \left(d_1, d_2\right)=\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1{ }^2} \sqrt{a_2{ }^2+b_2{ }^2}}
c) Khoảng cách từ $A\left(x_0 ; y_0\right)$ đến $B C$ : $a x_0+b y_0+c=0$ là
d(A, \Delta)=\frac{\left|a x_0+b y_0+c\right|}{\sqrt{a^2+b^2}}
a) Ta có:
$\overrightarrow{A B}=(10 ; 5), \overrightarrow{A C}=(6 ;-4), \overrightarrow{B C}=(-4 ;-9)$
+) Đường thẳng $A B$ nhận vectơ $\overrightarrow{A B}=(10 ; 5)$ làm
phương trình chỉ phương và đi qua điểm $A(-1 ; 1)$ nên có
phương trình tham số là: $\left\{\begin{array}{l}x=-1+10 t \\ y=1+5 t\end{array}\right.$
+) Đường thẳng $A C$ nhận vectơ $\overrightarrow{A C}=(6 ;-4)$ làm
phương trình chỉ phương và đi qua điểm $A(-1 ; 1)$ nên có
phương trình tham số là: $\left\{\begin{array}{l}x=-1+6 t \\ y=1-4 t\end{array}\right.$
+) Đường thẳng $B C$ nhận vectơ $\overrightarrow{B C}=(-4 ;-9)$ làm
phương trình chỉ phương và đi qua điểm $B(9 ; 6)$ nên có
phương trình tham số là: $\quad\left\{\begin{array}{l}x=9-4 t \\ y=6-9 t\end{array}\right.$
b) Ta có vectơ pháp tuyến của hai đường thẳng $A B$ và $A C$ lần lượt là: $\overrightarrow{n_1}=(1 ;-2), \overrightarrow{n_2}=(2 ; 3)$
\cos (A B, A C)=\cos \left(\overrightarrow{n_1}, \overrightarrow{n_2}\right)=\frac{|1.2+(-2) \cdot 3|}{\sqrt{1^2+(-2)^2} \sqrt{2^2+3^2}} \\ =\frac{4 \sqrt{65}}{65} \Rightarrow(A B, A C)=60^{\circ} 15^{\prime}
Vậy góc giữa hai đường thẳng $A B$ và $A C$ là $60^{\circ} 15^{\prime}$
c) Đường thẳng $B C$ nhận vectơ $\overrightarrow{B C}=(-4 ;-9)$ làm vectơ chỉ phương nên có vectơ pháp tuyến là
$\vec{n}=(9 ;-4)$ và đi qua $B(9 ; 6)$, suy ra phương trình tổng quát của đường thẳng $B C$ là:
9. $(x-9)-4(y-6)=0 \Leftrightarrow 9 x-4 y-57=0$
Khoảng cách từ $A(-1 ; 1)$ đến đường thẳng $B C$ là:
d(A, B C)=\frac{|9 .(-1)-4.1-57|}{\sqrt{9^2+(-4)^2}}=\frac{70 \sqrt{97}}{97}
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Đường thẳng trong mặt phẳng tọa độ Toán 10 Chân trời sáng tạo ở các trang 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





