Giải SGK bài Tọa độ vecto Toán 10 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Tọa độ Vecto. Đây là bài học thuộc bài 1 chương 9 trang 38, 39, 40, 41, 42, 43, 44, 45 sách Toán 10 Chân trời sáng tạo tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi SGK bài Tọa độ Vecto Toán 10 Chân trời sáng tạo
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 38, 39, 40, 41, 42, 43, 44, trong bài Tọa độ Vecto. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động khởi động trang 38

Bàn cờ được chia thành 8 hàng (1-8) và 8 cột (a-h) đánh số như hình vẽ.
Do đó mỗi quân cờ xác định khi biết số hàng và số cột, tương ứng với cặp số (x;y) trong đó x là số hàng, y là số cột.
Khi đó hai mã đen có vị trí là (8;b) và (4;e)
Hai mã trắng có vị trí là (3;c) và (3;f)
*Cách 2:
Đặt gốc tọa độ tại góc dưới, bên trái của bàn cờ. Coi mỗi ô vuông là 1 đơn vị.
Ta xác định được tọa độ của các con mã như sau:
Hai mã đen có tọa độ lần lượt là (2;8), (5;4)
Hai mã trắng có tọa độ lần lượt là (3;3) và (6;3)
Hoạt động khám phá 1 trang 38

+) Vectơ có độ lớn bằng 1 đơn vị, phương song song với trục Ox và cùng chiều với Ox
+) Vectơ \vec j có độ lớn bằng 1 đơn vị, phương song song với trục Oy và cùng chiều với Oy
Hoạt động khám phá 2 trang 38
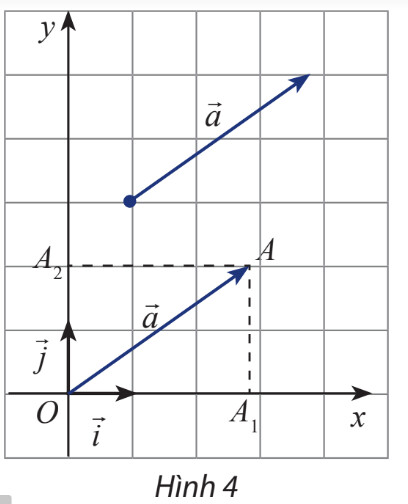
– Bước 1: Áp dụng quy tắc hình bình hành $\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{A D}$
– Bước 2: Dựa vào hình vẽ tìm $x, y$
– Bước 3: Biểu diễn vectơ $\vec{a}$
Áp dụng quy tắc hình bình hành ta có $\overrightarrow{O A}=\overrightarrow{O A_1}+\overrightarrow{O A_2}$
Dựa vào hình vẽ ta thấy $\overrightarrow{O A}_1=3 \vec{i}$ và $\overrightarrow{O A}_2=2 \vec{j}$
Vậy $\vec{a}=\overrightarrow{O A}=\overrightarrow{O A_1}+\overrightarrow{O A_2}=3 \vec{i}+2 \vec{j}$
Hoạt động khám phá 3 trang 39
Bước 1: Từ điểm $M(x ; y)$ xác định $M_1, M_2$ lần lượt là hình chiếu vuông góc của $M$ xuống trục hoành và trục tung
Bước 2: Tìm m, n sao cho $\overrightarrow{O M_1}=m .\vec{i} ; \overrightarrow{O M_2}=n .\vec{j}$
Bước 3: Dựa vào quy tắc hình bình hành, suy ra tọa độ của vectơ $\overrightarrow{O M}$ theo $\vec{i} ; \vec{j}$
Cho điểm $M(x ; y)$ bất kì, xác định $M_1, M_2$ lần lượt là hình chiếu vuông góc của $M$ xuống trục hoành và trục tung
Dễ thấy $\overrightarrow{O M_1}=x \vec{i} ; \overrightarrow{O M_2}=y \vec{j}$
Áp dụng quy tắc hình bình hành ta có $\overrightarrow{O M}=\overrightarrow{O M_1}+\overrightarrow{O M_2}=x \vec{i}+y \vec{j}$
Vậy tọa độ của vectơ $\overrightarrow{O M}$ là $(\mathrm{x} ; \mathrm{y})$, trùng với tọa độ điểm $\mathrm{M}$.
Thực hành 1 trang 40
a) Vẽ các điểm $D, E, F$ trên mặt phẳng $O x y$.
b) Tìm toạ độ của các vectoo $\overrightarrow{O D}, \overrightarrow{O E}, \overrightarrow{O F}$.
c) Vẽ và tìm toạ độ hai vectơ đơn vị $\vec{i}$ và $\vec{j}$ lần lượt trên hai trục toạ độ $O x$ và $O y$.
a)
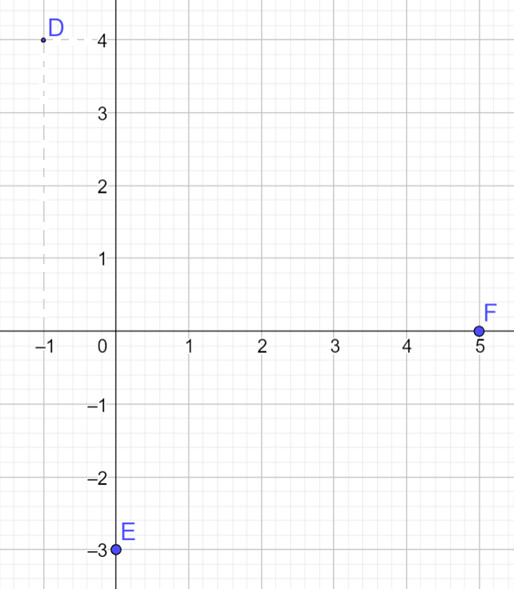
b) Vi tọa độ vectơ $\overrightarrow{O M}$ chính là tọa độ của điểm $M$ (với mọi $M$ ) nên ta có:
\overrightarrow{O D}=(-1 ; 4), \overrightarrow{O E}=(0 ;-3), \overrightarrow{O F}=(5 ; 0)
c)
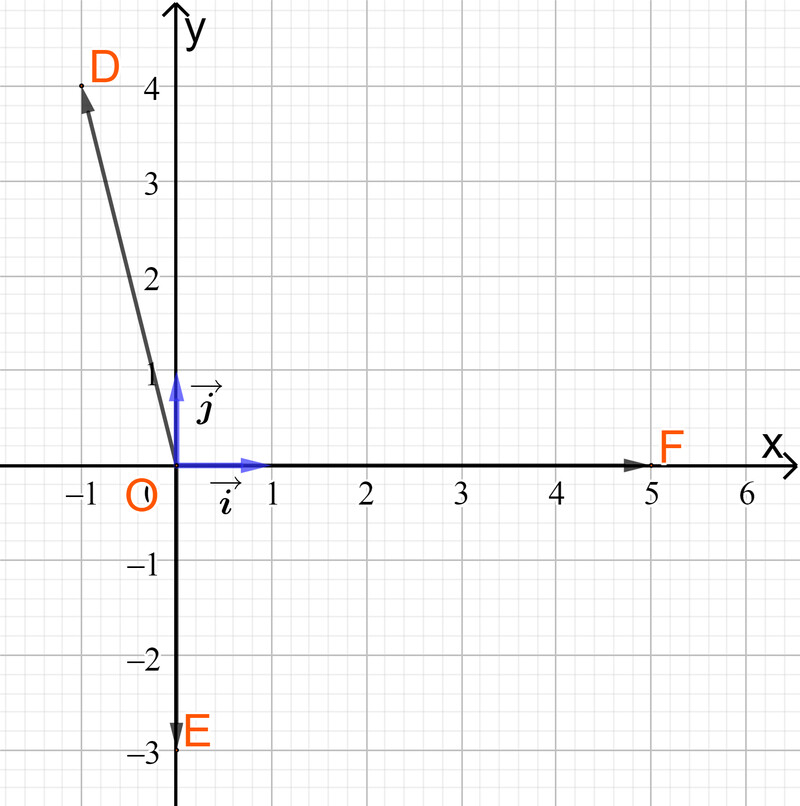
Từ hình vẽ ta có tọa độ của hai vectơ $\vec{i}$ và $\vec{j}$ là \vec{i}=(1 ; 0) và
\vec{j}=(0 ; 1)
Vận dụng 1 trang 40
a) Tính độ dài mỗi cạnh của hình chữ nhật $A B C D$.
b) Biểu diễn vectơ vận tốc $\vec{v}$ theo hai vectơ $\vec{i}$ và $\vec{j}$.
c) Tìm toạ độ của $\vec{v}$.
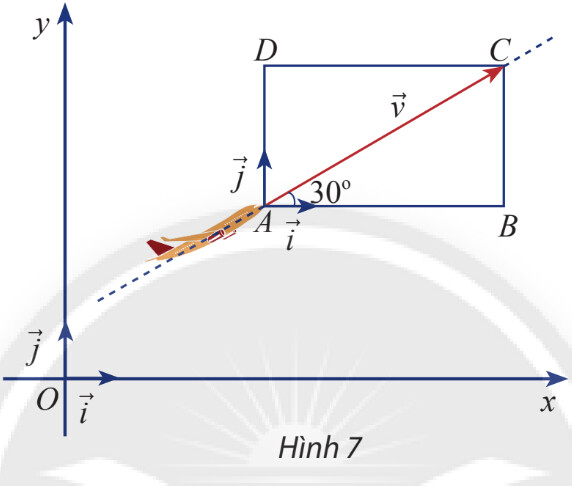
a) Vận tốc $240 \mathrm{~km} / \mathrm{h}$ nên $|\vec{v}|=A C=240$
Áp dụng các tính chất trong tam giác vuông ta có
A B=D C=A C .\cos (\widehat{C A B})=240 .\cos \left(30^{\circ}\right)=120 \frac{\sqrt{3}}{2} \\ A D=B C=A C .\sin (\widehat{C A B})=240 .\sin \left(30^{\circ}\right)=120
b) Xem $\mathrm{A}$ là gốc tọa độ nên ta có
\overrightarrow{A B}=120 \vec{i}, \overrightarrow{A D}=120 \frac{\sqrt{3}}{2} \vec{j}, \vec{v}=\overrightarrow{A C}=120 \vec{i}+120
c)
Ta có $\vec{v}=120 \vec{i}+120 \frac{\sqrt{3}}{2} \vec{j}$
Vậy tọa độ của vectơ $\vec{v}$ là $\left(120 ; 120 \frac{\sqrt{3}}{2}\right)$
Hoạt động khám phá 4 trang 40
a) Biểu diễn từng vectơ: $\vec{a}+\vec{b}, \vec{a}-\vec{b}, k \vec{a}$ theo hai vectơ $\vec{i}, \vec{j}$.
b) Tìm $\vec{a} \cdot \vec{b}$ theo toạ độ của hai vectơ $\vec{a}$ và $\vec{b}$.
a) Ta có
\vec{a}+\vec{b}=\left(a_1+a_2 \vec{j}\right)+\left(b_1+b_2 \vec{j}\right)=\left(a_1+b_1\right)+\left(a_2+b_2\right) \\ \vec{a}-\vec{b}=\left(a_1+a_2 \vec{j}\right)-\left(b_1+b_2 \vec{j}\right)=\left(a_1-b_1\right)+\left(a_2-b_2\right) \\ k \vec{a}=k\left(a_1+a_2 \vec{j}\right)=k a_1+k a_2 \vec{j}
b) Ta có
\vec{a} \cdot \vec{b}=\left(a_1 \vec{i}+a_2 \vec{j}\right) \cdot\left(b_1 \vec{i}+b_2 \vec{j}\right) \\ =a_1 b_1 \vec{i}^2+a_1 b_2 \vec{i} \cdot \vec{j}+a_2 b_1 \vec{i} \vec{j}+a_2 b_2 \vec{j}^2 \\ =a_1 b_1+a_2 b_2 \\ v_i \vec{i}^2=|\vec{i}|^2=1, \vec{j}^2=|\vec{j}|^2=1, \vec{i} \vec{j}=0
Thực hành 2 trang 41
a) Tìm toạ độ của các vectơ $\vec{m}+\vec{n}, \vec{m}-\vec{n}, 10 \vec{m},-4 \vec{n}$.
b) Tính các tích vô hướng $\vec{m} \cdot \vec{n},(10 \vec{m}) \cdot(-4 \vec{n})$.
Cho hai vectơ $\vec{a}=\left(a_1 ; a_2\right), \vec{b}=\left(b_1 ; b_2\right)$ và số thực $k$. Khi đó:
1) $\vec{a}+\vec{b}=\left(a_1+b_1 ; a_2+b_2\right)$;
3) $k \vec{a}=\left(k a_1 ; k a_2\right)$;
2) $\vec{a}-\vec{b}=\left(a_1-b_1 ; a_2-b_2\right)$
4) $\vec{a} \cdot \vec{b}=a_1 b_1+a_2 b_2$.
a) Ta có
\vec{m}+\vec{n}=((-6+0) ; 1+2)=(-6 ; 3) \\ \vec{m}-\vec{n}=((-6-0) ;(1-2))=(-6 ;-1) \\ 10 \vec{m}=(10 .(-6) ; 10 .1)=(-60 ; 10) \\ -4 \vec{n}=((-4) .0 ;(-4) .2)=(0 ;-8)
b) Ta có
\vec{m} .\vec{n}=(-6) .0+1.2=0+2=2
Ta có $10 \vec{m}=(-60 ; 10)$ và $-4 \vec{n}=(0 ;-8)$ nên
(10 \vec{m}) .(-4 \vec{n})=(-60) .0+10 .(-8)=0-80=-80
Vận dụng 2 trang 41
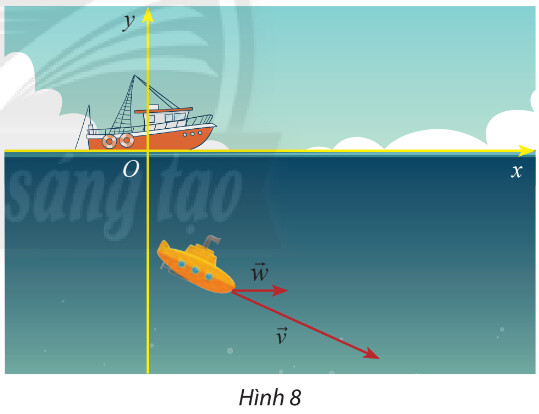
\text {Với } \vec{v}=\left(v_1 ; v_2\right), \vec{w}=\left(w_1 ; w_2\right) \text { thì } \vec{v}+\vec{w} \text { là } \\ \left(v_1+w_1 ; v_2+w_2\right)
\vec{v}+\vec{w}=(10+3,5 ;(-8)+0)=(13,5 ;-8)
Vậy tọa độ của vectơ tổng hai vận tốc $\vec{v}$ và $\vec{w}$ là $(13,5 ;-8)$
Hoạt động khám phá 5 trang 41
\text {Với } \vec{v}=\left(v_1 ; v_2\right), \vec{w}=\left(w_1 ; w_2\right) \text { thì } \vec{v}+\vec{w} \text { là } \\ \left(v_1+w_1 ; v_2+w_2\right)
Ta có tọa độ vectơ $\overrightarrow{O B}, \overrightarrow{O A}$ chính là tọa độ điểm $\mathrm{B}$ và $\mathrm{A}$
Nên ta có $\overrightarrow{O B}=\left(x_B ; y_B\right), \overrightarrow{O A}=\left(x_A ; y_A\right)$
\overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{O A}=\left(x_B ; y_B\right)-\left(x_A ; y_A\right)=\left(x_B-x_A ; y_B-y_A\right)
Thực hành 3 trang 42
\overrightarrow{A B}=\left(x_B-x_A ; y_B-y_A\right)
\overrightarrow{F E}=\left(x_E-x_F ; y_E-y_F\right)=(9-8 ; 9-(-7))=(1 ; 16) \\ \overrightarrow{F G}=\left(x_G-x_F ; y_G-y_F\right)=(0-8 ;(-6)-(-7))=(-8 ; 1) \\ \overrightarrow{E G}=\left(x_G-x_E ; y_G-y_E\right)=(0-9 ;(-6)-9)=(-9 ;-15)
Hoạt động khám phá 6 trang 42
a) Biểu thị vectơ $\overrightarrow{O M}$ theo hai vectơ $\overrightarrow{O A}$ và $\overrightarrow{O B}$.
b) Biểu thị vectơ $\overrightarrow{O G}$ theo ba vectơ $\overrightarrow{O A}, \overrightarrow{O B}$ và $\overrightarrow{O C}$.
c) Từ các kết quả trên, tìm toạ độ điểm $M$ và $G$ theo toạ độ của các điểm $A, B, C$.
a) Sử dụng tính chất trung điểm $\overrightarrow{O M}=\frac{1}{2}(\overrightarrow{O A}+\overrightarrow{O B})$ (với M là trung điểm của đoạn thẳng $A B$ )
b) Sử dụng tính chất trọng tâm $\overrightarrow{O G}=\frac{1}{3}(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})$ (với G là trọng tâm của tam giác $A B C$ )
c) Thay tọa độ các điểm vào và xác định
a) $\mathrm{M}$ là trung điểm của đoạn thẳng $A B$, áp dụng tính chất trung điểm
ta có:
\overrightarrow{O M}=\frac{1}{2}(\overrightarrow{O A}+\overrightarrow{O B})
b) G là trọng tâm của tam giác $A B C$, áp dụng tính chất trọng tâm của tam giác ta có:
\overrightarrow{O G}=\frac{1}{3}(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})
c) Ta có $\overrightarrow{O A}=\left(x_A ; y_A\right), \overrightarrow{O B}=\left(x_B ; y_B\right), \overrightarrow{O C}=\left(x_C ; y_C\right)$
Suy ra:
\overrightarrow{O M}=\frac{1}{2}(\overrightarrow{O A}+\overrightarrow{O B})=\frac{1}{2}\left[\left(x_A ; y_A\right)+\left(x_B ; y_B\right)\right] \\ =\left(\frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2}\right) \\ \overrightarrow{O G}=\frac{1}{3}(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})
=\frac{1}{3}\left[\left(x_A ; y_A\right)+\left(x_B ; y_B\right)+\left(x_c ; y_c\right)\right] \\ =\left(\frac{x_A+x_B+x_C}{3} ; \frac{y_A+y_B+y_C}{3}\right)
Mà ta có tọa độ vectơ $\overrightarrow{O M}$ chính là tọa độ điểm $\mathrm{M}$, nên ta có Tọa độ điểm $\mathrm{M}$ là $\left(x_M ; y_M\right)=\left(\frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2}\right)$
Tọa độ điểm $\mathrm{G}$ là $\left(\frac{x_A+x_B+x_C}{3} ; \frac{y_A+y_B+y_C}{3}\right)$
Thực hành 4 trang 43
a) Tìm toạ độ trung điểm $M$ của cạnh $Q S$.
b) Tìm toạ độ trọng tâm $G$ của tam giác $Q R S$.
Tọa độ điểm $\mathrm{M}$ là $\left(\frac{x_Q+x_S}{2} ; \frac{y_Q+y_S}{2}\right)$
Tọa độ điểm G là $\left(\frac{x_Q+x_R+x_S}{3} ; \frac{y_Q+y_R+y_S}{3}\right)$
a)
x_M=\frac{x_Q+x_S}{2}=\frac{7+(-2)}{2}=\frac{5}{2} ; \\ y_M=\frac{y_Q+y_S}{2}=\frac{(-2)+8}{2}=3
b)
x_G=\frac{x_Q+x_S+x_R}{3}=\frac{7+(-2)+(-4)}{3}=\frac{1}{3} ; \\ y_M=\frac{y_Q+y_S+y_R}{3}=\frac{(-2)+8+9}{3}=5 \\ \text { Vậy } G\left(\frac{1}{3} ; 5\right)
Hoạt động khám phá 7 trang 43
a) $\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} .\vec{b}=0 \Leftrightarrow a_{1} b_{1}+a_{2} b_{2}=?$.
b) $\vec{a}$ và $\vec{b}$ cùng phương $\Leftrightarrow\left\{\begin{array}{l}a_{1}=t b_{1} \\ a_{2}=t b_{2}\end{array}\right.$ hay $\left\{\begin{array}{l}b_{1}=k a_{1} \\ b_{2}=k a_{2}\end{array} \Leftrightarrow a_{1} b_{2}-a_{2} b_{1}=. ?\right.$.;
c) $|\vec{a}|=\sqrt{(\vec{a})^{2}}=\sqrt{?}$
d) $\overrightarrow{A B}=\left(x_{B}-x_{A} ; y_{B}-y_{A}\right) \Rightarrow A B=\sqrt{(\overrightarrow{A B})^{2}}=\sqrt{?}$.
e) $\cos (\vec{a}, \vec{b})=\frac{\vec{a} .\vec{b}}{|\vec{a}| .|\vec{b}|}=\frac{?}{\sqrt{a_{1}^{2}+a_{2}^{2}} \cdot \sqrt{b_{1}^{2}+b_{2}^{2}}}(\vec{a}, \vec{b}$ khác $\overrightarrow{0})$
a) $\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} .\vec{b}=\overrightarrow{0} \Leftrightarrow a_1 b_1+a_2 b_2=0$
b) $\vec{a}$ và $\vec{b}$ cùng phương $\Leftrightarrow\left\{\begin{array}{l}a_1=t b_1 \\ a_2=t b_2\end{array}\right.$ hay $\left\{\begin{array}{l}b_1=k a_1 \\ b_2=k a_2\end{array}\right.$ $\Leftrightarrow a_1 b_2-a_2 b_1=a_1 .k a_2-a_2 .k a_1=0$
c) $|\vec{a}|=\sqrt{(\vec{a})^2}=\sqrt{a_1^2+a_2^2}$
d) $\overrightarrow{A B}=\left(x_B-x_A ; y_B-y_A\right) \Rightarrow A B=\sqrt{(\overrightarrow{A B})^2}$ $=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}$
\text { e) } \cos (\vec{a}, \vec{b})=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot|\vec{b}|}=\frac{a_1 b_1+a_2 b_2}{\sqrt{a_1{ }^2+a_2^2} \cdot \sqrt{b_1^2+b_2^2}}
Thực hành 5 trang 44
a) Tìm toạ độ điểm $H$ là chân đường cao của tam giác $D E F$ kẻ từ $D$.
b) Giải tam giác $D E F$.
Bước 1: Tìm tọa độ các vectoo $\overrightarrow{D H}, \overrightarrow{E F}$
Bước 2: Dựa vào ứng dụng tọa độ của các phép toán vectơ (tính chất vuông góc)
a) Ta có: $\overrightarrow{E F}=(-2 ; 4)$
Gọi tọa độ điểm H là $(x ; y)$ ta có
\overrightarrow{D H}=(x-2 ; y-2), \overrightarrow{E H}=(x-6 ; y-2)
$\mathrm{H}$ là chân đường cao nên $\overrightarrow{D H} \perp \overrightarrow{E F}$
\overrightarrow{D H} \perp \overrightarrow{E F} \Leftrightarrow(x-2) \cdot(-2)+(y-2) .4=0 \\ \Leftrightarrow-2 x+4 y-4=0
Hai vectơ $\overrightarrow{E H}, \overrightarrow{E F}$ cùng phương
\Leftrightarrow(x-6) \cdot(-2)-(y-2) \cdot 4=0 \Leftrightarrow-2 x-4 y+20=0 (2)
Từ (1) và (2) ta có hệ phương trình
\left\{\begin{array} { l } { – 2 x + 4 y – 4 = 0 } \\ { – 2 x – 4 y + 2 0 = 0 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=4 \\ y=3 \end{array}\right.\right.
Vậy $H(4 ; 3)$
b) Ta có: $\overrightarrow{D E}=(4 ; 0), \overrightarrow{D F}=(0 ; 4), \overrightarrow{E F}=(-4 ; 4)$
Suy ra:
D E=|\overrightarrow{D E}|=\sqrt{4^2+0^2}=4, D F=|\overrightarrow{D F}|=\sqrt{0^2+4^2}=4 \\ \quad E F=|\overrightarrow{E F}|=\sqrt{(-4)^2+4^2}=4 \sqrt{2} \\ \cos D=\cos (\overrightarrow{D E}, \overrightarrow{D F})=\frac{\overrightarrow{D E} .\overrightarrow{D F}}{D E .D F}=\frac{4 .0+0.4}{4 .4}=0 \Rightarrow \widehat{D}=90^{\circ} \\ \cos E=\cos (\overrightarrow{E D}, \overrightarrow{E F})=\frac{\overrightarrow{E D} .\overrightarrow{E F}}{E D .E F}=\frac{(-4) .(-4)+0 .4}{4 .4 \sqrt{2}}=\frac{\sqrt{2}}{2} \Rightarrow \widehat{E} = 45^o
Vận dụng 3 trang 44
a) Tính số đo của $\widehat{B A C}$.
b) Cho biết một đơn vị trên hệ trục toạ độ tương ứng với $1 \mathrm{~km}$. Tính khoảng cách từ con tàu đến mỗi hòn đảo.
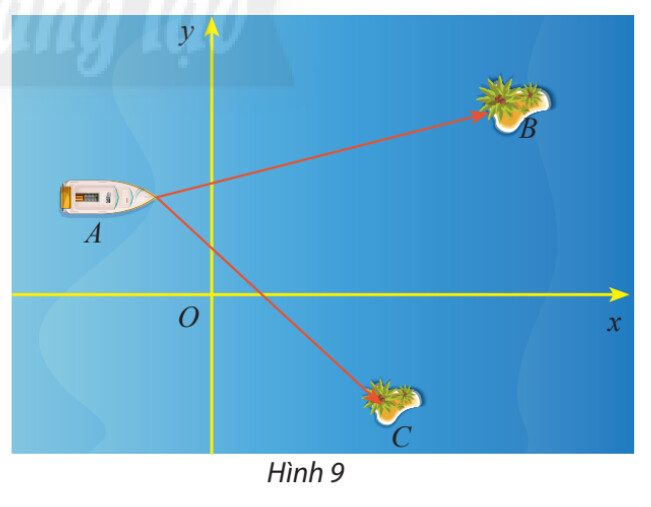
Bước 1: Xác định tọa độ các vectơ $\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{B C}$
Bước 2:
a) $\cos \widehat{B A C}=\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{\overrightarrow{A B} \cdot \overrightarrow{A C}}{A B \cdot A C}$
b) $A B=|\overrightarrow{A B}|=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}$
\text {a) Ta có: } \overrightarrow{A B}=(60 ; 10), \overrightarrow{A C}=(42 ;-43), \overrightarrow{B C}=(-18 ;-53) \\ \cos \widehat{B A C}=\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{\overrightarrow{A B} \cdot \overrightarrow{A C}}{A B \cdot A C}=\frac{60.42+10 \cdot(-43)}{\sqrt{60^2+10^2} \cdot \sqrt{42^2+(-43)^2}} \\ \simeq 0,572 \Rightarrow \widehat{B A C} \approx 55^{\circ} 8^{\prime}
b)
Khoảng cách từ tàu đến đảo B là A B=|\overrightarrow{A B}|=\sqrt{60^2+10^2}=10 \sqrt{37}(\mathrm{~km})
Khoảng cách từ tàu đến đảo $\mathrm{B}$ làA C=|\overrightarrow{A C}|=\sqrt{42^2+(-43)^2}=\sqrt{3613}(\mathrm{~km})
Giải bài tập SGK bài Tọa độ Vecto Toán 10 Chân trời sáng tạo
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 44, 45 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Tọa độ vecto ở trên.
Bài 1 trang 44
a) Vẽ trục và biểu diễn các điểm đã cho lên trên trục đó.
b) Hai vectơ $\overrightarrow{A B}$ và $\overrightarrow{C D}$ cùng hướng hay ngược hướng?
Bước 1: Tìm tọa độ $\overrightarrow{A B}$ và $\overrightarrow{C D}$
Bước 2: Xác định tỉ lệ tọa độ của các vectơ $\overrightarrow{A B}=k \overrightarrow{C D}$
Nếu $k>0$ thì hai vectơ cùng hướng
Nếu $k<0$ thì hai vectơ ngược hướng
a)

b) Ta có: Tọa độ các vectơ $\overrightarrow{A B}$ và $\overrightarrow{C D}$ lần lượt là: $-5 ; 5$
Ta có $\overrightarrow{A B}=-\overrightarrow{C D}$
Vậy hai vectơ $\overrightarrow{A B}$ và $\overrightarrow{C D}$ ngược hướng
Bài 2 trang 45
a) $\vec{a}=(4 ;-6)$ và $\vec{b}=(-2 ; 3)$ là hai vectơ ngược hướng.
b) $\vec{a}=(-2 ; 3)$ và $\vec{b}=(-8 ; 12)$ là hai vectơ cùng hướng.
c) $\vec{a}=(0 ; 4)$ và $\vec{b}=(0 ;-4)$ là hai vectơ đối nhau.
Cho $\overrightarrow{A B}=k \overrightarrow{C D}$
Nếu $k>0$ thì hai vectơ cùng hướng
Nếu $k<0$ thì hai vectơ ngược hướng
Nếu $k=-1$ thì hai vectơ đối nhau
a) Ta thấy
$4=(-2) .(-2) ;-6=(-2) .3 \Rightarrow \vec{a}=-2 \vec{b}$
$-20$ nên hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng (đpcm)
c) Ta thấy $0=-1.0 ; 4=(-1) .(-4) \Rightarrow \vec{a}=-\vec{b}$
Suy ra hai vectơ $\vec{a}$ và $\vec{b}$ đối nhau (đpcm)
Bài 3 trang 45
a) $\vec{a}=2 \vec{i}+7 \vec{j}$
b) $\vec{b}=-\vec{i}+3 \vec{j}$;
c) $\vec{c}=4 \vec{i}$
d) $\vec{d}=-9 \vec{j}$
\text { Vectơ } \vec{a}=a_1 \vec{i}+a_2 \vec{j} \text { có tọa độ là }\left(a_1 ; a_2\right)
a) Tọa độ của vectơ $\vec{a}$ là $(2 ; 7)$
b) Tọa độ của vectơ $\vec{b}$ là $(-1 ; 3)$
c) Tọa độ của vectơ $\vec{c}$ là $(4 ; 0)$
d) Tọa độ của vectơ $\vec{d}$ là $(0 ;-9)$
Bài 4 trang 45
a) Thuộc trục hoành;
b) Thuộc trục tung;
c) Thuộc đường phân giác của góc phần tư thứ nhất.
a) Điểm thuộc trục hoành có tung độ bằng 0
b) Điểm thuộc trục tung có hoành độ bằng 0
c) Điểm thuộc góc phần tư thứ nhất có tung độ bằng hoành độ
a) Vì điểm thuộc hoành độ có tung độ bằng 0 nên ta có điểm B thuộc trục hoành
b) Vì điểm thuộc tung độ có hoành độ bằng 0 nên ta có điểm C thuộc trục tung
c) Vì điểm thuộc góc phần tư thứ nhất có tung độ bằng hoành độ nên ta có điểm thuộc đường phân giác góc phần tư thứ nhất là điểm D
Bài 5 trang 45
a) Điểm $H$ là hình chiếu vuông góc của điểm $M$ trên trục $O x$;
b) Điểm $M^{\prime}$ đối xứng với $M$ qua trục $O x$;
c) Điểm $K$ là hình chiếu vuông góc của điểm $M$ trên trục $O y$;
d) Điểm $M^{\prime \prime}$ dối xứng với $M$ qua trục $O y$;
e) Điểm $C$ dối xứng với $M$ qua gốc toạ độ.
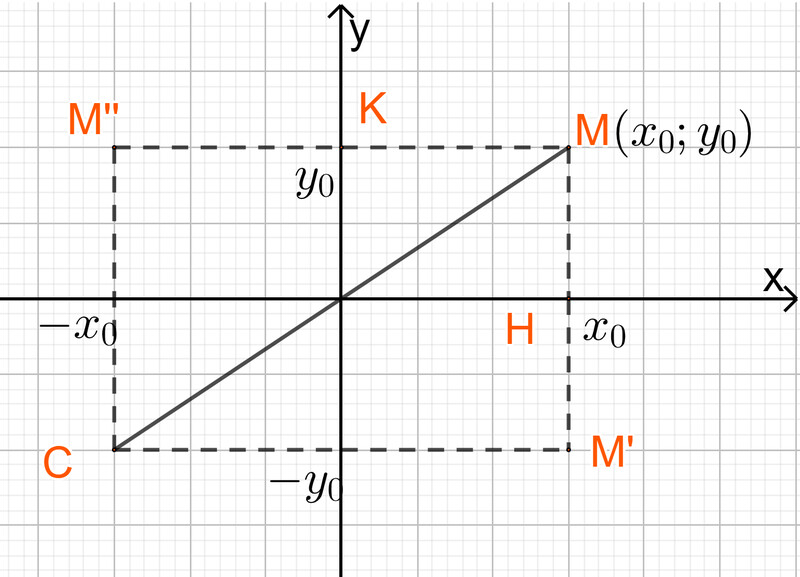
a) $\mathrm{H}$ là hình chiếu vuông góc của $M$ trên trục $O x$ nên tọa độ điểm H là $H\left(x_0 ; 0\right)$
b) $\mathrm{M}^{\prime}$ đối xứng với $\mathrm{M}$ qua trục $\mathrm{Ox}$ nên $\mathrm{H}$ là trung điểm của $\mathrm{MM}^{\prime}$
Suy ra $x_{M^{\prime}}=2 x_H-x_M=2 x_0-x_0=x_0 ; y_{M^{\prime}}=2 y_H-y_M$ $=2.0-y_0=-y_0$
Vậy tọa độ điểm $\mathrm{M}^{\prime}$ là $\left(x_0 ;-y_0\right)$
c) $K$ là hình chiếu vuông góc của $M$ trên trục Oy nên tọa độ điểm K là $K\left(0 ; y_0\right)$
d) $\mathrm{M}^{\prime \prime}$ đối xứng với $\mathrm{M}$ qua trục Oy nên $\mathrm{K}$ là trung điểm của $\mathrm{MM}^{\prime \prime}$
Suy ra
x_{M^{\prime \prime}}=2 x_K-x_M=2.0-x_0=-x_0 ; y_{M^{\prime \prime}}=2 y_K -y_M=2 y_0-y_0=y_0
Vậy tọa độ điểm $\mathrm{M}^{\prime \prime}$ là $\left(-x_0 ; y_0\right)$
e) C đối xứng với $\mathrm{M}$ qua gốc tọa độ nên $\mathrm{O}$ là trung điểm của MC
Suy ra
x_C=2 x_O-x_M=2.0-x_0=-x_0 ; y_C=2 y_O-y_M =2.0-y_0=-y_0
Vậy tọa độ điểm C là $\left(-x_0 ;-y_0\right)$
Bài 6 trang 45
a) Tìm toạ độ điểm $D$ sao cho $A B C D$ là một hình bình hành.
b) Tìm toạ độ giao điểm hai đường chéo của hình bình hành $A B C D$.
c) Giải tam giác $A B C$.
a) Bước 1: Xác định tọa độ vectơ $\overrightarrow{A B}, \overrightarrow{D C}$
Bước 2: Áp dụng quy tắc hình bình hành $\overrightarrow{A B}=\overrightarrow{D C}$ (hai vectơ bằng nhau thì tọa độ tương ứng của chúng bằng nhau)
b) Áp dụng tính chất trung điểm
c) Sử dụng ứng dụng biểu thức tọa độ của các phép toán vectơ
a) Gọi tọa độ của điểm D là $(x ; y)$ ta có: $\overrightarrow{A B}=(1 ; 3)$, $\overrightarrow{D C}=(5-x ; 5-y)$
Để $A B C D$ là hình bình hành thì $\overrightarrow{A B}=\overrightarrow{D C}$
Suy ra $\left\{\begin{array}{l}5-x=1 \\ 5-y=3\end{array} \Rightarrow\left\{\begin{array}{l}x=4 \\ y=2\end{array}\right.\right.$
Vậy để $A B C D$ là hình bình hành thì tọa độ điểm $D$ là $D(4 ; 2)$
b) Gọi M à giao điểm của hai đường chéo, suy ra M là trung điểm của $A C$
Suy ra:
x_M=\frac{x_A+x_C}{2}=\frac{2+5}{2}=\frac{7}{2} ; y_M=\frac{y_A+y_C}{2}=\frac{2+5}{2}=\frac{7}{2}
Vậy tọa đọ giao điểm của hai đường chéo hình bình hành $\mathrm{ABCD}$ là $M\left(\frac{7}{2} ; \frac{7}{2}\right)$
\text { c) Ta có: } \overrightarrow{A B}=(1 ; 3), \overrightarrow{A C}=(3 ; 3), \overrightarrow{B C}=(2 ; 0) \\ \text { Suy ra: } \\ A B=|\overrightarrow{A B}|=\sqrt{1^2+3^2}=\sqrt{10}, A C=|\overrightarrow{A C}| \\ =\sqrt{3^2+3^2}=3 \sqrt{2} \\ B C=|\overrightarrow{B C}|=\sqrt{2^2+0^2}=2 \\ \cos A=\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{\overrightarrow{A B} \cdot \overrightarrow{A C}}{A B \cdot A C}=\frac{1 \cdot 3+3 \cdot 3}{\sqrt{10} \cdot 3 \sqrt{2}}=\frac{2 \sqrt{5}}{5} \\ \Rightarrow \widehat{A} \approx 26^{\circ} 33^{\prime} \\ \cos B=\cos (\overrightarrow{B A}, \overrightarrow{B C})=\frac{\overrightarrow{B A} \cdot \overrightarrow{B C}}{B A \cdot B C}=\frac{(-1) \cdot 2+(-3) 0}{\sqrt{10} \cdot 2}= \\ -\frac{\sqrt{10}}{10} \Rightarrow \widehat{B}=108^{\circ} 26^{\prime} \\ \widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-26^{\circ} 33^{\prime}-108^{\circ} 26^{\prime} \\ =45^{\circ} 1^{\prime} \\
Bài 7 trang 45
a) Tìm toạ độ các đỉnh của tam giác $A B C$.
b) Chứng minh rằng trọng tâm của các tam giác $A B C$ và $M N P$ trùng nhau.
c) Giải tam giác $A B C$.
a) Tọa độ trung điểm $\mathrm{M}$ của $\mathrm{AB}$ là:
M=\left(\frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2}\right)
b) Tọa độ trọng tâm của tam giác $A B C$ là:
G=\left(\frac{x_A+x_B+x_C}{3} ; \frac{y_A+y_B+y_C}{3}\right)
Tọa độ trọng tâm của tam giác MNP là:
G^{\prime}=\left(\frac{x_M+x_N+x_P}{3} ; \frac{y_M+y_N+y_P}{3}\right)
a) Gọi tọa độ các điểm như sau:
$A\left(x_A ; y_A\right), B\left(x_B ; y_B\right), C\left(x_C ; y_C\right)$
$M(2 ; 2), N(3 ; 4), P(5 ; 3)$ lần lượt là trung điểm của các cạnh $A B, B C$ và $C A$ nên ta có:
\left\{\begin{array} { l } { x _ { A } + x _ { B } = 2 x _ { M } = 4 } \\ { x _ { A } + x _ { C } = 2 x _ { P } = 1 0 } \\ { x _ { C } + x _ { B } = 2 x _ { N } = 6 } \\ { y _ { A } + y _ { B } = 2 y _ { M } = 4 } \\ { y _ { A } + y _ { C } = 2 y _ { P } = 8 } \\ { y _ { C } + y _ { B } = 2 y _ { N } = 6 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x_A+x_B=4 \\ x_C-x_B=6 \\ x_C+x_B=6 \\ y_A+y_B=4 \\ y_C-y_B=4 \\ y_C+y_B=6 \end{array}\right.\right.
\Leftrightarrow\left\{\begin{array}{l} x_A=4 \\ x_B=0 \\ x_C=6 \\ y_A=3 \\ y_B=1 \\ y_C=5 \end{array}\right.
Vậy các đỉnh của tam giác có tọa độ là $A(4 ; 3), B(0 ; 1), C(6 ; 5)$
b) Gọi $G\left(x_G ; y_G\right), G^{\prime}\left(x_{G^{\prime}} ; y_{G^{\prime}}\right)$ là trọng tâm của hai tam giác $A B C$ và $M N P$
Áp dụng tính chất trọng tâm ta có:
x_G=\frac{x_A+x_B+x_C}{3} =\frac{4+0+6}{3}=\frac{10}{3} \\ y_G=\frac{y_A+y_B+y_C}{3} =\frac{3+1+5}{3}=3 \\ x_{G^{\prime}}=\frac{x_M+x_N+x_P}{3} =\frac{2+3+5}{3}=\frac{10}{3} \\ y_{G^{\prime}}=\frac{y_M+y_N+y_P}{3} =\frac{2+4+3}{3}=3
Suy ra $G\left(\frac{10}{3} ; 3\right)$ và $G^{\prime}\left(\frac{10}{3} ; 3\right)$, tọa độ của chúng bằng nhau nên hai điểm $G$ và $G^{\prime}$ trùng nhau (đpcm)
c) Ta có: $\overrightarrow{A B}=(-4 ;-2), \overrightarrow{A C}=(2 ; 2), \overrightarrow{B C}=(6 ; 4)$
Suy ra:
A B=|\overrightarrow{A B}|=\sqrt{(-4)^2+(-2)^2}=2 \sqrt{5}, \\ AC=|\overrightarrow{A C}|=\sqrt{2^2+2^2}=2 \sqrt{2} \\ B C=|\overrightarrow{B C}|=\sqrt{6^2+4^2}=2 \sqrt{13} \\ \cos A=\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{\overrightarrow{A B} .\overrightarrow{A C}}{A B .A C}=\frac{(-4) .2+(-2) .2}{2 \sqrt{5} .2 \sqrt{2}}= -\frac{3 \sqrt{10}}{10} \Rightarrow \widehat{A} \approx 161^{\circ} 33^{\prime} \\ \cos B=\cos (\overrightarrow{B A}, \overrightarrow{B C})=\frac{\overrightarrow{B A} \cdot \overrightarrow{B C}}{B A .B C}=\frac{4.6+2.4}{2 \sqrt{5} .2 \sqrt{13}} =\frac{8 \sqrt{65}}{65} \Rightarrow \widehat{B}=7^{\circ} 7^{\prime} \\ \widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-161^{\circ} 33^{\prime}-7^{\circ} 7^{\prime} =11^{\circ} 20^{\prime} \\
Bài 8 trang 45
a) Tìm toạ độ điểm $D$ nằm trên trục $O x$ sao cho $D A=D B$.
b) Tính chu vi tam giác $O A B$.
c) Chứng minh rằng $O A$ vuông góc với $A B$ và từ đó tính diện tích tam giác $O A B$.
a) Gọi tọa độ điểm $D$ là $(x ; 0)$
Ta có:
\overrightarrow{D B}=(4-x ; 2) \Rightarrow D B=|\overrightarrow{D B}|=\sqrt{(4-x)^2+2^2} \\ D A=D B \Leftrightarrow \sqrt{(1-x)^2+3^2}=\sqrt{(4-x)^2+2^2} \\ \Rightarrow(1-x)^2+3^2=(4-x)^2+2^2 \\ \Rightarrow x^2-2 x+10=x^2-8 x+20 \\ \Rightarrow 6 x=10 \\ \Rightarrow x=\frac{5}{3}
Thay $x=\frac{5}{3}$ ta thấy thảo mãn phương trình
Vậy khi $D\left(\frac{5}{3} ; 0\right)$ thì $D A=D B$
b) Ta có:
\overrightarrow{O A}=(1 ; 3) \Rightarrow OA=|\overrightarrow{OA}|= \sqrt{1^2+3^2}=\sqrt{10}
\overrightarrow{O B}=(4 ; 2) \Rightarrow O B=|\overrightarrow{O B}|=\sqrt{4^2+2^2}=2 \sqrt{5}
\overrightarrow{A B}=(3 ;-1) \Rightarrow A B=|\overrightarrow{A B}|=\sqrt{3^2+(-1)^2} \\ =\sqrt{10}
Chu vi tam giác $O A B$ là
C_{O A B}=O A+O B+A B=\sqrt{10}+2 \sqrt{5}+\sqrt{10} \\ =2 \sqrt{10}+2 \sqrt{5}
c) $\overrightarrow{O A} \cdot \overrightarrow{A B}=1 \cdot 3+3 \cdot(-1)=0 \Rightarrow O A \perp A B$
Tam giác $O A B$ vuông tại $A$ nên diện tích của tam giác là
S_{O A B}=\frac{1}{2} O A \cdot A B=\frac{1}{2} \sqrt{10} \cdot \sqrt{10}=5
Bài 9 trang 45
a) $\vec{a}=(2 ;-3), \vec{b}=(6 ; 4)$;
b) $\vec{a}=(3 ; 2), \vec{b}=(5 ;-1)$
c) $\vec{a}=(-2 ;-2 \sqrt{3}), \vec{b}=(3 ; \sqrt{3})$.
\text { +) } \cos (\vec{a}, \vec{b})=\frac{\vec{a} .\vec{b}}{|\vec{a}| .|\vec{b}|} \\ \text { +) } \vec{a} .\vec{b}=x_a .x_b+y_a .y_b \\ \text { +) }|\vec{a}|=\sqrt{x_a^2+y_a^2}
a)\cos (\vec{a}, \vec{b})=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| .|\vec{b}|}=\frac{2 .6+(-3) .4}{\sqrt{2^2+(-3)^2} .\sqrt{6^2+4^2}}=0 \Rightarrow \vec{a} \perp \vec{b} \\ b) \cos (\vec{a}, \vec{b})=\frac{\vec{a} .\vec{b}}{|\vec{a}| .|\vec{b}|}=\frac{3 .5+2 .(-1)}{\sqrt{3^2+2^2} . \sqrt{5^2+(-1)^2}}=\frac{\sqrt{2}}{2} \\ \Rightarrow(\vec{a}, \vec{b})=45^{\circ}\\ c) \cos (\vec{a}, \vec{b})=\frac{\vec{a} .\vec{b}}{|\vec{a}| .|\vec{b}|}=\frac{(-2) .3+(-2 \sqrt{3}) .\sqrt{3}}{\sqrt{(-2)^2+(-2 \sqrt{3})^2} .\sqrt{3^2+\sqrt{3}^2}}=-\frac{\sqrt{3}}{2} \\ \Rightarrow(\vec{a}, \vec{b})=150^{\circ}
Bài 10 trang 45
Bước 1: Tính độ dài các cạnh thông qua độ dài vecto => tứ giác là hình thoi
Bước 2: Chỉ ra một góc vuông thông qua tích vô hướng => đpcm
Ta có: $\overrightarrow{A B}=(1 ; 7), \overrightarrow{A D}=(-7 ; 1), \overrightarrow{C D}=(-1 ;-7)$ $\overrightarrow{B C}=(-7 ; 1)$
Suy ra
A B=\overrightarrow{A B}=\sqrt{1^2+7^2}=5 \sqrt{2}, A D=\overrightarrow{A D} \\ =\sqrt{(-7)^2+1^2}=5 \sqrt{2}, \\ \quad C D=\overrightarrow{C D}=\sqrt{(-1)^2+(-7)^2}=5 \sqrt{2}, \\ B C=\overrightarrow{B C}=\sqrt{(-7)^2+(-1)^2}=5 \sqrt{2} \\ \Rightarrow A B=B C=C D=D A=5 \sqrt{2}(1)
Mặt khác ta có
\cos (\overrightarrow{A B}, \overrightarrow{A D})=\frac{\overrightarrow{A B} .\overrightarrow{A D}}{A B .A D}=\frac{1 .(-7)+7.1}{5 \sqrt{2} .5 \sqrt{2}}=0 \Rightarrow \widehat{A} \\ =90^{\circ}
Từ (1) và( 2 ) suy ra $A B C D$ là hình vuông (đpcm)
Bài 11 trang 45
Vectơ tổng hai vận tốc $\vec{v}$ và $\overrightarrow{\mathrm{w}}$ là:
\vec{v}+\overrightarrow{\mathrm{w}}=(-222 ;-46)
Khi đó độ dài của hai vectơ là $|\overrightarrow{\mathrm{v}}+\overrightarrow{\mathrm{w}}|=\sqrt{(-222)^2+(-46)^2}=10 \sqrt{514}(\mathrm{~km})$.
Vậy độ dài tổng hai vẫn tốc $\vec{v}$ và $\overrightarrow{\mathrm{w}}$ là $10 \sqrt{514}(\mathrm{~km})$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Tọa độ vecto Toán 10 Chân trời sáng tạo tập 2 ở các trang 38, 39, 40, 41, 42, 43, 44, 45. Chúc các bạn có một buổi học thật thú vị và bổ ích!





