Giải SGK bài Xác suất của biến cố Toán 10 Chân trời sáng tạo tập 2
Xác suất của biến cố là bài học thuộc bài 2 chương 10 Toán 10 Chân trời sáng tạo tập 2. Dưới đây là những lời giải cực chi tiết của HocThatGioi cho những hoạt động khám phá, thực hành, vận dụng cũng như bài tập sách giáo khoa ở các trang 81, 82, 83, 84, 85 mà các bạn sẽ được học trong bài này. Cùng theo dõi ngay nhé!
Trả lời câu hỏi SGK bài Xác suất của biến cố
Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng ở các trang 81, 82, 83, 84 sẽ giúp bạn tiếp thu kiến thức về bài học Xác suất của biến cố một cách dễ dàng hơn rất nhiều. Tham khảo ngay lời giải của HocThatGioi nhé!
Hoạt động khám phá 1 trang 81
A: “Mặt xuất hiện có số chấm là số chẵn”,
B: “Mặt xuất hiện có số chấm là số lẻ”.
Vî con xúc xắc cân đối và đồng chất nên các mặt có khả năng xuất hiện như nhau
Tập hợp mô tả biến cố $A$ là: 2, 4, 6 suy ra có 3 kết quả thuận lợi cho biến cố $A$
Tập hợp mô tả biến cố $B$ là: 1, 3, 5 suy ra có 3 kết quả thuận lợi cho biến cố $B$
Vậy khả năng xảy ra của hai biến cố $A$ và $B$ là như nhau
Thực hành 1 trang 82
a) “Hai mặt xuất hiện có cùng số chấm”;
b) “Tổng số chấm trên hai mặt xuất hiện bằng 9 “.
Bước 1: Xác định không gian mẫu
Bước 2: Xác định số kết quả thuận lợi của biến cố
Bước 3: Tính xác xuất bằng công thức $P(A)=\frac{n(A)}{n(\Omega)}$
Kết quả của mỗi lần thử là một cặp $(i ;$ j $)$ với i và j lần lượt là số chấm xuất hiện trên hai xúc xắc, hai con xúc xắc gieo đồng thời nên không quan tâm thứ tự, ta có không gian mẫu là:
\Omega = \{(1 ; 1),(1 ; 2),(1 ; 3),(1 ; 4),(1 ; 5),(1 ; 6),\\ (2 ; 2),(2 ; 3),(2 ; 4), (2 ; 5),(2 ; 6),\\ (3 ; 3),(3 ; 4),(3 ; 5),(3 ; 6), \\ (4 ; 4),(4 ; 5),(4 ; 6),\\ (5 ; 5),(5 ; 6),(6 ; 6)\}
Không gian mẫu gồm có 21 kết quả, tức là $n(\Omega)=21$
a) Ta có tập hợp miêu tả biến cố $A$
A=\{(1 ; 1),(2 ; 2),(3 ; 3),(4 ; 4),(5 ; 5),(6 ; 6)\} \Rightarrow n(A)=6
Do đó, xác suất của biến cố $A$ là: $\quad P(A)=\frac{n(A)}{n(\Omega)}=\frac{6}{21}=\frac{2}{7}$
b) Ta có tập hợp miêu tả biến cố $B$
B=\{(6 ; 3),(5 ; 4)\} \Rightarrow n(B)=2
Do đó, xác suất của biến cố $B$ là: $\quad P(B)=\frac{n(B)}{n(\Omega)}=\frac{2}{21}$
Vận dụng trang 83
Bước 1: Xác định không gian mẫu
Bước 2: Xác định số kết quả thuận Iợi của biến cố
Bước 3: Tính xác xuất bằng công thức $P(A)=\frac{n(A)}{n(\Omega)}$
Do các viên bi có cùng kích thước và trọng lượng nên số kết quả cho việc lấy 2 viên bi từ hộp có 10 viên bi có $C_{10}^2$ cách
Gọi $A$ là biến cố “Lấy được hai viên bi cùng màu”
Việc lấy được hai viên bi cùng màu có hai khả năng
+) Khả năng thứ nhất: hai viên bi cùng màu xanh có $C_5^2$ cách
+) Khả năng thứ hai: hai viên bi cùng màu đỏ có $C_5^2$ cách
Suy ra có $2 C_5^2=20$ kết quả thuận lợi cho biến cố $A$
Vậy xác suất của biến cố $A$ là: $P(A)=\frac{n(A)}{n(\Omega)}=\frac{20}{C_{10}^2}=\frac{4}{9}$ Gọi Blà biến cố “Lấy được hai viên bi khác màu”
Việc lấy được hai viên bi khác màu có hai công đoạn
+) Công đoạn thứ nhất: Lấy 1 viên bi màu xanh có 5 cách
+) Công đoạn thứ hai: Lấy 1 viên bi màu đỏ có 5 cách
Suy ra có $5.5=25$ kết quả thuận lợi cho biến cố $B$
Vậy xác suất của biến cố $B$ là: $P(B)=\frac{n(B)}{n(\Omega)}=\frac{25}{C_{10}^2}=\frac{5}{9}$
Thực hành 2 trang 83
Gọi A là biến cố “Không bạn nào lấy đúng thẻ của mình”
Các kết quả có thể xảy ra khi các bạn lần lượt lấy thẻ được thể hiện ở sơ đồ hình cây như hình dưới
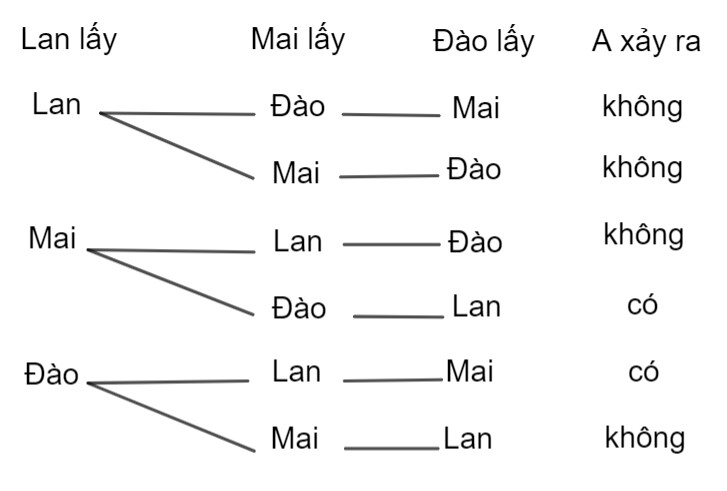
Có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho $A$, do đó:
P(A)=\frac{2}{6}=\frac{1}{3}
Hoạt động khám phá 2 trang 84
Bước 1: Xác định không gian mẫu
Bước 2: Xác định số kết quả thuận lợi của biến cố
Bước 3: Tính xác xuất bằng công thức $P(A)=\frac{n(A)}{n(\Omega)}$
Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có $C_{10}^3=120$ cách, suy ra $n(\Omega)=120$
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố $A$ ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có
5. $C_5^2=50$ khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có $C_5^2 .5=50$ khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có $C_5^3=10$ khả năng
Suy ra $n(A)=50+50+10=110$
Vậy xác suất của biến cố $\mathrm{A}$ là: $P(A)=\frac{110}{120}=\frac{11}{12}$
Thực hành 3 trang 84
a) “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3 “;
b) “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc lớn hơn 4 “.
Bước 1: Xác định biến cố đối của biến cố đã cho
Bước 2: Xác định xác suất của biến cố đã xác định ở bước 1
Bước 3: Xác định biến cố ban đầu
a) Gọi biến cố $A$ : “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc không chia hết cho 3″ là biến cố đối của biến cố ‘Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3”
Tổng số kết quả của phép thử có thể xảy ra là $n(\Omega)=6^3$
$A$ xảy ra khi mặt xuất hiện trên ba con xúc xắc đều xuất hiện số chấm không chi hết cho 3. Số kết quả thuận lợi cho $\mathrm{A}$ là: $n(A)=4^3$
Xác suất của biến cố $A$ là: $P(A)=\frac{n(A)}{n(\Omega)}=\frac{4^3}{6^3}=\frac{8}{27}$
Vậy xác suất của biến cố “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho $3^{\prime \prime}$ là $1-\frac{8}{27}=\frac{19}{27}$
b) Gọi biến cố B: “Tổng các số chấm ở mặt xuất hiện trên ba con súc sắc nhỏ hơn hoặc bằng 4” là biến cố đối của biến cố “Tổng các số chấm ở mặt xuất hiện trên ba con súc sắc lớn hơn $4^{\prime \prime}$
Tổng số kết quả của phép thử có thể xảy ra là $n(\Omega)=6^3$
Ta có tập hợp kết quả thuận lợi cho biến cố $B$ như sau: $B=\{(1 ; 1 ; 1),(1 ; 1 ; 2)\}$. Số kết quả thuận lợi cho $B$ là: $n(A)=2$
Xác suất của biến cố $A$ là: $P(A)=\frac{n(A)}{n(\Omega)}=\frac{2}{6^3}=\frac{1}{108}$
Vậy xác suất của biến cố “Tổng các số chấm ở mặt xuất hiện trên ba con súc sắc lớn hơnn $4^{\prime \prime}$ là $1-\frac{1}{108}=\frac{107}{108}$
Thực hành 4 trang 84
a) có it nhất 1 bi xanh.
b) có ít nhất 2 bi đỏ.
Bước 1: Xác định biến cố đối của biến cố đã cho
Bước 2: Xác định xác suất của biến cố đã xác định ở bước 1
Bước 3: Xác định biến cố ban đầu
Tổng số kết quả của phép thử có thể xảy ra là $n(\Omega)=C_{12}^4=495$
a) Gọi biến cố $A$ : “Trong 4 viên bi lấy ra có ít nhất 1 bi xanh”, suy ra biến cố đối của biến cố $A$ là $\bar{A}$ : “Trong 4 viên bi lấy ra không có viên bi xanh nào”
$\bar{A}$ xảy ra khi 4 viên bi lấy ra chỉ có màu đỏ hoặc vàng. Số kết quả thuận lợi cho $\bar{A}$ là: $n(A)=C_9^4=126$
Xác suất của biến cố $\bar{A}$ là: $P(\bar{A})=\frac{n(\bar{A})}{n(\Omega)}=\frac{126}{495}=\frac{14}{55}$
Vậy xác suất của biến cố $A$ là $P(A)=1-P(\bar{A})=1-\frac{14}{55}=\frac{41}{55}$
b) Gọi biến cố $A$ : “Trong 4 viên bi lấy ra có ít nhất 2 bi đỏ “, suy ra biến cố đối của biến cố $A$ là $\bar{A}$ : “Trong 4 viên bi lấy ra có nhiều hơn 2 bi đỏ”
$\bar{A}$ xảy ra khi 4 viên bi lấy ra có 3 hoặc 4 bi đỏ. Số kết quả thuận lợi cho $\bar{A}$ là: $n(A)=C_4^3 .8+C_4^4=33$
Xác suất của biến cố $\bar{A}$ là: $P(\bar{A})=\frac{n(\bar{A})}{n(\Omega)}=\frac{33}{495}=\frac{1}{15}$
Vậy xác suất của biến cố $A$ là $P(A)=1-P(\bar{A})=1-\frac{1}{15}=\frac{14}{15}$
Hoạt động khám phá 3 trang 84
Vì 10 kg gạo tẻ có rất nhiều hạt, trong khi lấy 1 hạt từ rất rất nhiều thì khả năng lấy được hạt gạo nếp rất nhỏ, có thể xem như không xảy ra. Nên theo em, hạt gạo được lấy ra là gạo tẻ.
Giải bài tập SGK bài Xác suất của biến cố
Những bài tập SGK ở cuối bài Xác suất của biến cố trang 85 sách Toán 10 Chân trời sáng tạo sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 1 trang 85
a) “Xuất hiện ba mặt sấp”;
b) “Xuất hiện it nhất một mặt sấp”.
a) Biến cố đối của biến cố “Xuất hiện ba mặt sấp” là biến cố: “Xuất hiện ba mặt ngửa”
b) Biến cố đối của biến cố “Xuất hiện ít nhất một mặt sấp” là biến cố “Không xuất hiện mặt sấp nào”
Bài 2 trang 85
a) “Tổng số chấm xuất hiện nhỏ hơn 10 “;
b) “Tích số chấm xuất hiện chia hết cho 3 “.
Bước 1: Xác định không gian mẫu
Bước 2: Xác định biến cố đối
Bước 3: Tính xác suất của biến cố đối bằng công thức $P(A)=\frac{n(A)}{n(\Omega)}$
Bước 4: Xác định xác suất của biến cố ban đầu
Tổng số kết quả có thể xảy ra của phép thứ là $n(\Omega)=6^2$
a) Gọi biến cố $A$ “Tổng số chấm xuất hiện lớn hơn hoặc bằng 10″ là biến cố đối của biến cố “Tổng số chấm xuất hiện nhỏ hơn 10”
A xảy ra khi số chấm xuất hiện là 5 hoặc 6 . Số kết quả thuận lợi cho $A$ là $n(A)=2^2$
Xác suất của biến cố $A$ là $P(A)=\frac{2^2}{6^2}=\frac{1}{9}$
Vậy xác suất của biến cố “Tổng số chấm xuất hiện nhỏ hơn $10^{\prime \prime}$ là $1-\frac{1}{9}=\frac{8}{9}$
b) Gọi biến cố $A$ : “Tích số chấm xuất hiện không chia hết cho 3” là biến cố đối của biến cố ““Tích số chấm xuất hiện chia hết cho 3”
$A$ xảy ra khi mặt xuất hiện trên hai con xúc xắc đều xuất hiện số chấm không chia hết cho 3. Số kết quả thuận lợi cho $\mathrm{A}$ là: $n(A)=4^2$
Xác suất của biến cố $A$ là: $P(A)=\frac{n(A)}{n(\Omega)}=\frac{4^2}{6^2}=\frac{4}{9}$
Vậy xác suất của biến cố “Tích số chấm xuất hiện chia hết cho $3^{\prime \prime}$ là $1-\frac{4}{9}=\frac{5}{9}$
Bài 3 trang 85
a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thế xảy ra.
b) Tính xác suất của biến cố “Trong 2 thẻ lấy ra có it nhất 1 thẻ màu đỏ”.
a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
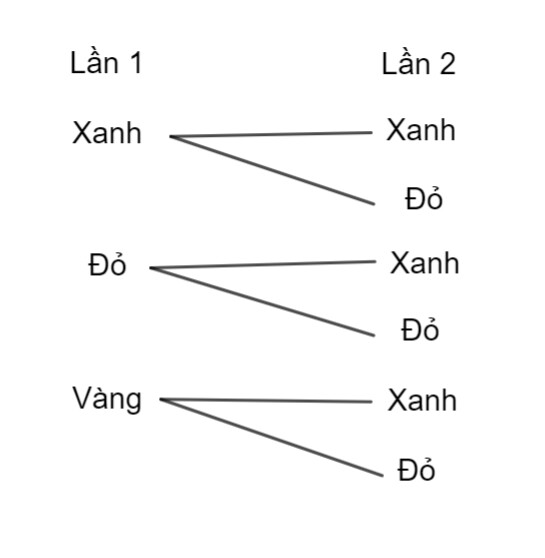
b)
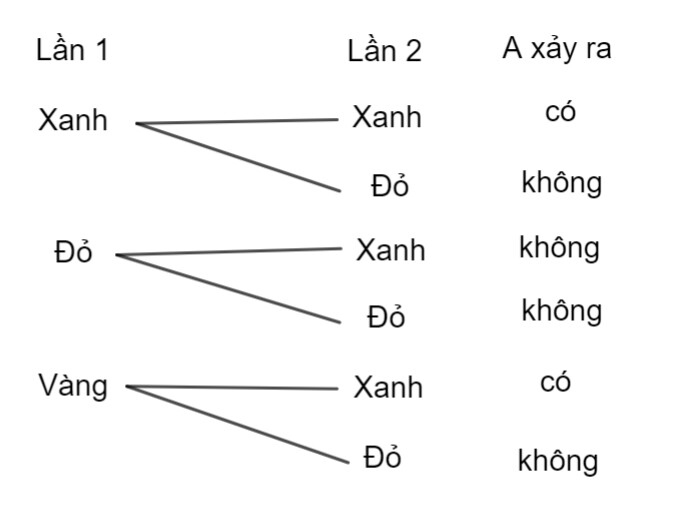
Gọi $A$ là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho $I$. Do đó:
P(A)=\frac{2}{6}=\frac{1}{3}
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là $1-\frac{1}{3}=\frac{2}{3}$
Bài 4 trang 85
Ta thấy hai biến cố :”Hai quả bóng lây ra cùng màu” và “Hai quả bóng lấy ra khác màu” là hai biến cố đối
Suy ra xác suất của biến cố “Hai quả bóng lây ra cùng màu” là $1-0,6=0,4$
Bài 5 trang 85
a) “Nhân và Tín không đứng cạnh nhau”;
b) “Trí không đứng ở đầu hàng”.
Bước 1: Xác định không gian mẫu
Bước 2 : Xác định biến cố đối
Bước 3: Tính xác suất của biến cố đối bằng công thức $P(A)=\frac{n(A)}{n(\Omega)}$
Bước 4:Xác định xác suất của biến cố ban đầu
Tổng số kết quả có thể xảy ra của phép thử là $n(\Omega)=5$ !
a) Gọi biến cố $A$ “Nhân và Tín đứng cạnh nhau” là biến cố đối của biến cố “Nhân và Tín không đứng cạnh nhau” Số kết quả thuận lợi cho $A$ là: $n(A)=2 ! \cdot 3 ! \cdot 2^3$
Xác suất của biến cố $A$ là: $P(A)=\frac{n(A)}{n(\Omega)}=\frac{2 ! .3 ! .2^3}{5 !}=\frac{4}{5}$
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là $1-\frac{4}{5}=\frac{1}{5}$
b) Gọi biến cố $A$ “Trí đứng ở đầu hàng” là biến cố đối của biến cố “Trí không đứng ở đầu hàng”
Số kết quả thuận Iợi cho $\mathrm{A}$ là: $n(A)=4 ! .2$
Xác suất của biến cố $A$ là: $P(A)=\frac{n(A)}{n(\Omega)}=\frac{4 ! .2}{5 !}=\frac{2}{5}$
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là $1-\frac{2}{5}=\frac{3}{5}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Xác suất của biến cố Toán 10 Chân trời sáng tạo tập 2 ở các trang 81, 82, 83, 84, 85. Hi vọng các bạn sẽ có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





