Giải SGK bài Ba đường Conic Toán 10 Cánh diều tập 2
Trong bài viết này, HocThatGioi sẽ giải đáp những câu hỏi và bài tập trong bài Ba đường Conic. Đây là bài học thuộc Bài 6 Chương VII trang 93, 94, 95, 96, 97, 98, 99, 100, 101, 102 sách Toán 10 Cánh diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Ba đường Conic Toán 10 Cánh diều tập 2
Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng sẽ giúp bạn dễ dàng tiếp thu kiến thức về bài học Ba đường Conic.
Câu hỏi khởi động trang 93
Đường conic gồm những loại đường nào và được xác định như thế nào?
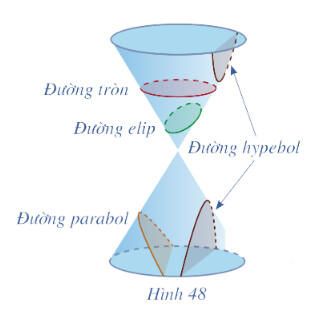
Đường conic gồm 3 loại đường đó là: elip, hypebol, parabol
Luyện tập vận dụng 1 trang 95
Elip có phương trình chính tắc là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$
Do Elip đi qua điểm $\mathrm{M}(0 ; 3)$ nên $b=3$
Điểm $N\left(3 ;-\frac{12}{5}\right)$ thuộc (E) nên ta có: $\frac{3^2}{a^2}+\frac{\left(-\frac{12}{5}\right)^2}{3^2}=1 \Leftrightarrow a=5$
Vậy Elip có phương trình chính tắc là: $\frac{x^2}{25}+\frac{y^2}{9}=1$
Hoạt động 4 trang 97
Tương tự elip, ta chọn trục $O x$ là đường thẳng $F_{1} F_{2}$, trục $O y$ là đường trung trực của đoạn thẳng $F_{1} F_{2}=2 c(c>0)$, gốc toạ độ $O$ là trung điểm của đoạn thẳng $F_{1} F_{2}$ (Hình 54).
a) Tìm tọa độ của hai tiêu điểm $F_{1}, F_{2}$.
b) Nêu dự đoán thích hợp cho ? trong bảng sau:

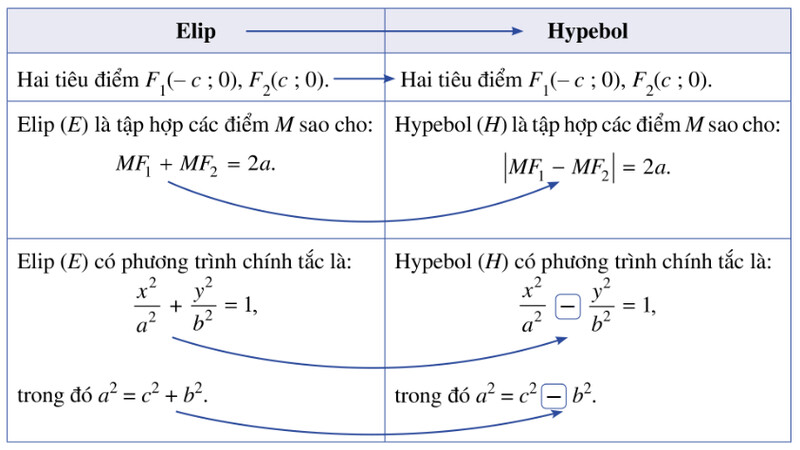
Luyện tập vận dụng 2 trang 98
Ta có: $4 x^2-9 y^2=1 \Leftrightarrow \frac{x^2}{\left(\frac{1}{4}\right)^2}-\frac{y^2}{\left(\frac{1}{9}\right)^2}=1$
Vậy phương trình chính tắc của hypebol là: $\frac{x^2}{\left(\frac{1}{4}\right)^2}-\frac{y^2}{\left(\frac{1}{9}\right)^2}=1$
Luyện tập vận dụng 3 trang 100
a) $x=\frac{y^2}{4}$
b) $x-y^2=0$
a) $x=\frac{y^2}{4} \Leftrightarrow y^2=4 x$
Vậy dạng chính tắc của parabol là: $y^2=4 x$
b) $x-y^2=0 \Leftrightarrow y^2=x$
Vậy dạng chính tắc của parabol là: $y^2=x$
Giải bài tập SGK bài Ba đường Conic Toán 10 Cánh diều tập 2
Sau khi đã tìm hiểu phần nội dung của bài học, cùng ôn lại những kiến thức đã học qua phần giải đáp chi tiết các bài tập trong SGK Toán 10 Cánh diều tập 2 trang 102 dưới đây nhé.
Bài tập 1 trang 102
$a)\frac{x^{2}}{64}+\frac{y^{2}}{64}=1$
$b)\frac{x^{2}}{64}-\frac{y^{2}}{64}=1$
$c)\frac{x^{2}}{64}+\frac{y^{2}}{25}=1$
$d)\frac{x^{2}}{25}+\frac{y^{2}}{64}=1$
Elip (E) có phương trình chính tắc là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$
Phương trình chính tắc của elip là: c) $\frac{x^2}{64}+\frac{y^2}{25}=1$.
a) Không là PTCT vì $a=b=8$
b) Không là PTCT
d) Không là PTCT vì $\mathrm{a}=5<\mathrm{b}=8$.
Bài tập 2 trang 102
Elip (E) giao với 2 trục tọa độ Ox, Oy tại bốn điểm $A_1(-a ; 0),$ $A_2(a ; 0),$ $B_1(0 ;-b),$ $B_2(0 ; b)$
Elip (E) có 2 tiêu điểm là $F_1(-c ; 0)$ và $F_2(c ; 0)$ trong đó $a^2=c^2+b^2$
Từ phương trình chính tắc của (E) ta có: $a=7, b=5
Ta có: $c^2=a^2-b^2=7^2-5^2=24$
Suy ra: c= \sqrt{24} =2 \sqrt{6}
Vậy ta có tọa độ các giao điểm của (E) với trục $O x$, Oy là: $A_1(-7 ; 0),$ $A_2(7 ; 0),$ $B_1(0 ;-5),$ $B_2(0 ; 5)$
Hai tiêu điểm của (E) có tọa độ là: $F_1(-2 \sqrt{6} ; 0), F_2(2 \sqrt{6} ; 0)$
Bài tập 3 trang 102
Elip (E) giao với 2 trục tọa độ Ox, Oy tại bốn điểm $A_1(-a ; 0),$ $A_2(a ; 0),$ $B_1(0 ;-b),$ $B_2(0 ; b)$
Do (E) giao với $\mathrm{Ox}$ tại $A_1(-5 ; 0)$ nên ta có: $a=5$
Do (E) giao với Oy tại $B_2(0 ; \sqrt{10})$ nên ta có: $b=\sqrt{10}$
Vậy phương trình chính tắc của (E) là: $\frac{x^2}{25}+\frac{y^2}{10}=1$
Bài tập 4 trang 102
Viết phương trình chính tắc của elip đó.
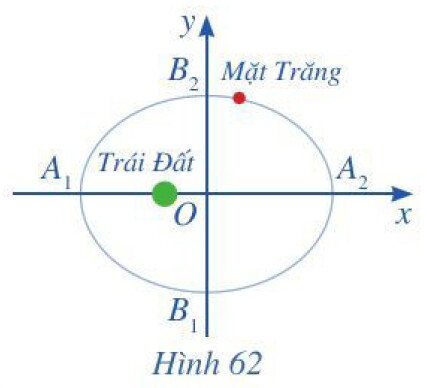
Elip (E) có phương trình chính tắc là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$, trong đó: $A_1 A_2=2 a, B_1 B_2=2 b$
Ta có:
$$A_1 A_2=2 a \Rightarrow 2 a=768800 \Rightarrow a=384400 \text { và } B_1 B_2=2 b \Rightarrow 767619=2 b \Rightarrow b=383809,5$$
Vậy phương trình chính tắc của (E) là: $\frac{x^2}{384400^2}+\frac{y^2}{383809,5}=1$
Bài tập 5 trang 102
a) $\frac{x^{2}}{9}+\frac{y^{2}}{9}=1$
b) $\frac{x^{2}}{9}-\frac{y^{2}}{9}=1$
c) $\frac{x^{2}}{9}-\frac{y^{2}}{64}=1$
d) $\frac{x^{2}}{64}-\frac{y^{2}}{9}=1$.
Hypebol (H) có phương trình chính tắc là: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó $a^2=c^2-b^2$
Những phương trình là phương trình chính tắc của $(\mathrm{H})$ là: b), c), d).
Bài tập 6 trang 102
a) $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$
b) $\frac{x^{2}}{36}-\frac{y^{2}}{25}=1$.
Hypebol $(\mathrm{H})$ có phương trình chính tắc là: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó $a^2=c^2-b^2$
a) Ta có: $a=3, b=4 \Rightarrow c=\sqrt{3^2+4^2}=5$
Vậy tiêu điểm của (E) là: $F_1(-5 ; 0), F_2(5 ; 0)$
b) Ta có: $a=6 ; b=5 \Rightarrow c=\sqrt{6^2+5^2}=\sqrt{61}$
Vậy tiêu điểm của (E) là: $F_1(-\sqrt{61} ; 0), F_2(\sqrt{61} ; 0)$
Bài tập 7 trang 102
Hypebol (H) có phương trình chính tắc là: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó $a^2=c^2-b^2$ Hypebol (H) giao với trục Ox tại hai tiêu điểm.
Do hypebol (H) giao với trục $\mathrm{Ox}$ tại điểm có hoành độ bằng 3 nên ta có: $F_1(3 ; 0) \Rightarrow c=3 \Rightarrow a^2+b^2=9(1)$
Do $N(\sqrt{10} ; 2) \in(H)$ nên ta có: $\frac{10}{a^2}-\frac{4}{b^2}=1(2)$
Từ $(1),(2)$ ta có: $a=\sqrt{5}, b=2$
Vậy phương trình chính tắc của $(\mathrm{H})$ là: $\frac{x^2}{5}-\frac{y^2}{4}=1$
Bài tập 8 trang 102
a) $y^{2}=-2 x$
b) $y^{2}=2 x$;
c) $x^{2}=-2 y$
d) $y^{2}=\sqrt{5} x$.
Phương trình chính tắc của parabol là: $y^2=2px(p \gt 0)$
Những phương trình chính tắc của parabol là: b), d)
Bài tập 9 trang 102
a) $y^{2}=\frac{5 x}{2}$
b) $y^{2}=2 \sqrt{2} x$
Phương trình chính tắc của parabol là: $y^2=2 p x(p>0)$, trong đó tiêu điểm là $F\left(\frac{p}{2} ; 0\right)$ và phương trình đường chuẩn là: $x+\frac{p}{2}=0$.
a) Tiêu điểm của parabol là: $F\left(\frac{5}{4} ; 0\right)$
Phương trình đường chuẩn là: $x+\frac{5}{4}=0$
b) Tiêu điểm của parabol là: $F(\sqrt{2} ; 0)$
Phương trình đường chuẩn là: $x+\sqrt{2}=0$
Bài tập 10 trang 102
Phương trình chính tắc của parabol là: $y^2=2 p x(p>0)$, trong đó tiêu điểm là $F\left(\frac{p}{2} ; 0\right)$ và phương trình đường chuẩn là: $x+\frac{p}{2}=0$.
Do parabol có tiêu điểm là $F(6 ; 0)$ nên ta có $\frac{p}{2}=6 \Leftrightarrow p=12$
Vậy phương trình chính tắc của parabol là: $y^2=24 x$
Bài tập 11 trang 102
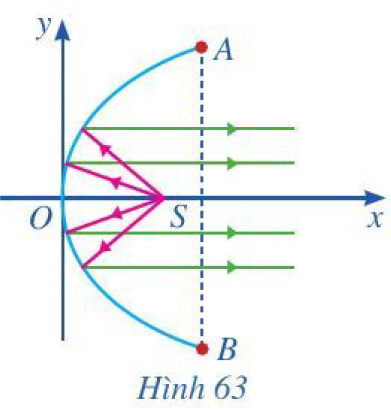
Phương trình chính tắc của parabol là: $y^2=2 p x(p>0)$, trong đó tiêu điểm là $F\left(\frac{p}{2} ; 0\right)$ và phương trình đường chuẩn là: $x+\frac{p}{2}=0$.
Gọi phương trình chính tắc của parabol là: $y^2=2 p x(p>0)$
Vì $A B=40 \mathrm{~cm}$ và $h=30 \mathrm{~cm}$ nên $A(30 ; 20)$
Do $A(30 ; 20)$ thuộc parabol nên ta có: $20^2=2 p .30 \Rightarrow p=\frac{20}{3}$
Vậy parabol có phương trình chính tắc là: $y^2=\frac{40}{3} x$
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài 6 Chương VII Phương pháp toạ độ trong mặt phẳng trang 93, 94, 95, 96, 97, 98, 99, 100, 101, 102 sách Toán 10 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!





