SGK Toán 7 – Kết Nối Tri Thức
Giải SGK Bài tập cuối chương 3 trang 59 Toán 7 Kết nối tri thức tập 1
Các bài tập cuối chương 3 trang 59 SGK Toán 7 kết nối tri thức tập 1 sẽ giúp các bạn ôn tập lại các kiến thức về Góc và đường thẳng song song một cách chi tiết nhất. Cùng xem HocThatGioi giải quyết các bài toán này nhé!
Bài 3.32 trang 59 Toán 7 Toán 7 Kết nối tri thức tập 1
Chứng minh rằng: Cho điểm $A$ và đường thẳng $d$ thì có duy nhất đường thẳng đi qua $A$ vuông góc với $d$, tức là nếu có hai đường thẳng đi qua $A$ vuông góc với $d$ thì chủng phải trùng nhau.
Phương pháp giải:
Giả sử có 2 đường thẳng đi qua A và vuông góc với d. Ta sẽ chứng minh 2 đường này trùng nhau.
Giả sử có 2 đường thẳng đi qua A và vuông góc với d. Ta sẽ chứng minh 2 đường này trùng nhau.
Lời giải chi tiết:
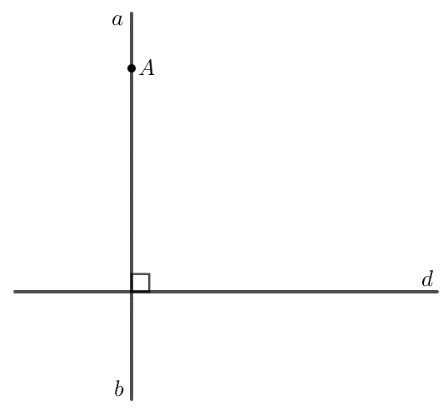
Gọi $a$ và $b$ lần lượt là hai đường thẳng đi qua $\mathrm{A}$ và vuông góc với $d$.
Do $a$ và $b$ cùng vuông góc với $d$ nên $a / / b$ hoặc $a$ trùng $b$.
Mà $a$ và $b$ cắt nhau tại $A$ nên $a$ không thể song song với $b$.
Do đó $a$ trùng $b$.
Vậy cho điểm $\mathrm{A}$ và đường thẳng $\mathrm{d}$ thì có duy nhất đường thẳng đi qua $\mathrm{A}$ vuông góc với d.

Gọi $a$ và $b$ lần lượt là hai đường thẳng đi qua $\mathrm{A}$ và vuông góc với $d$.
Do $a$ và $b$ cùng vuông góc với $d$ nên $a / / b$ hoặc $a$ trùng $b$.
Mà $a$ và $b$ cắt nhau tại $A$ nên $a$ không thể song song với $b$.
Do đó $a$ trùng $b$.
Vậy cho điểm $\mathrm{A}$ và đường thẳng $\mathrm{d}$ thì có duy nhất đường thẳng đi qua $\mathrm{A}$ vuông góc với d.
Bài 3.33 trang 59 Toán 7 Toán 7 Kết nối tri thức tập 1
Vẽ ba đường thẳng phân biệt $a, b, c$ sao cho $a / / b, b / / c$ và hai đường thẳng phân biệt $m, n$ cùng vuông góc với $a$. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?
Lời giải chi tiết:
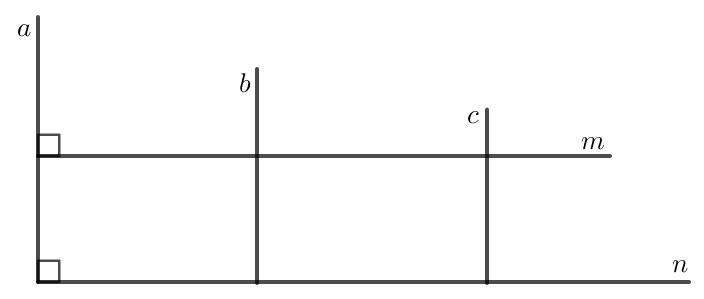
Do $a / / b, b / / c$ nên $a / / c$.
Do $m \perp a, n \perp a$ nên $m / / \mathrm{n}$.
Các cặp đường thẳng song song là: $\mathrm{a}-\mathrm{b}, \mathrm{b}-\mathrm{c}, \mathrm{a}-\mathrm{c}, \mathrm{m}-\mathrm{n}$.
Do đó trên hình có 4 cặp đường thẳng song song.
Do a$ // b$, $m \perp a$ nên $m \perp b$.
Do $a / / c$, $m \perp a$ nên $m \perp c$.
Do $a // b$, $n \perp a$ nên $n \perp b$.
Do $a // c$, $n \perp a$ nên $n \perp c$.
Các cặp đường thẳng vuông góc là: $m-a, m-b, m-c, n-a, n-b, n-c$.
Do đó trên hình có 6 cặp đường thẳng vuông góc.

Do $a / / b, b / / c$ nên $a / / c$.
Do $m \perp a, n \perp a$ nên $m / / \mathrm{n}$.
Các cặp đường thẳng song song là: $\mathrm{a}-\mathrm{b}, \mathrm{b}-\mathrm{c}, \mathrm{a}-\mathrm{c}, \mathrm{m}-\mathrm{n}$.
Do đó trên hình có 4 cặp đường thẳng song song.
Do a$ // b$, $m \perp a$ nên $m \perp b$.
Do $a / / c$, $m \perp a$ nên $m \perp c$.
Do $a // b$, $n \perp a$ nên $n \perp b$.
Do $a // c$, $n \perp a$ nên $n \perp c$.
Các cặp đường thẳng vuông góc là: $m-a, m-b, m-c, n-a, n-b, n-c$.
Do đó trên hình có 6 cặp đường thẳng vuông góc.
Bài 3.34 trang 59 Toán 7 Toán 7 Kết nối tri thức tập 1
Cho Hình 3.50 , trong đó hai tia $A x, B y$ nằm trên hai đường thẳng song song. Chứng minh rằng $\widehat{C}=\widehat{A}+\widehat{B}$.
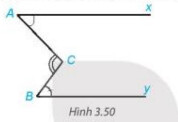
Lời giải chi tiết:
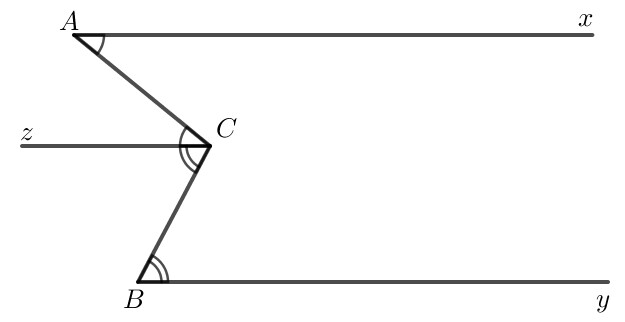
Kẻ tia $Cz$ song song với $A x$, do đó $C z$ song song với $By$.
Do $\mathrm{Ax}$ song song với $\mathrm{Cz}$ nên $\widehat{C A x}=\widehat{A C z}$ (2 góc so le trong).
Do By song song với $\mathrm{Cz}$ nên $\widehat{C B y}=\widehat{B C z}$ (2 góc so le trong).
Khi đó $\widehat{A C \mathrm{z}}+\widehat{B C \mathrm{z}}=\widehat{C A x}+\widehat{C B y}$.
hay $\widehat{C}=\widehat{A}+\widehat{B}$.
Vậy ta có điều phải chứng minh.

Kẻ tia $Cz$ song song với $A x$, do đó $C z$ song song với $By$.
Do $\mathrm{Ax}$ song song với $\mathrm{Cz}$ nên $\widehat{C A x}=\widehat{A C z}$ (2 góc so le trong).
Do By song song với $\mathrm{Cz}$ nên $\widehat{C B y}=\widehat{B C z}$ (2 góc so le trong).
Khi đó $\widehat{A C \mathrm{z}}+\widehat{B C \mathrm{z}}=\widehat{C A x}+\widehat{C B y}$.
hay $\widehat{C}=\widehat{A}+\widehat{B}$.
Vậy ta có điều phải chứng minh.
Bài 3.35 trang 59 Toán 7 Toán 7 Kết nối tri thức tập 1
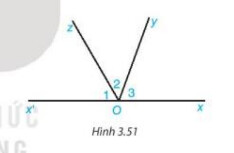
Cho Hình 3.51 , trong đó $O x$ và $O x^{\prime}$ là hai tia đối nhau.
a) Tính tổng số đo ba góc $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$.
Gơi ý: $\widehat{O_{1}}+\widehat{O_{2}}+\widehat{O_{3}}=\left(\widehat{O_{1}}+\widehat{O_{2}}\right)+\widehat{O_{3}}$,
trong đó $\widehat{O_{1}}+\widehat{O_{2}}=\widehat{x^{\prime} O y}$.
b) Cho $\widehat{O_{1}}=60^{\circ}, \widehat{O_{3}}=70^{\circ}$. Tinh $\widehat{O_{2}}$.
a) Tính tổng số đo ba góc $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$.
Gơi ý: $\widehat{O_{1}}+\widehat{O_{2}}+\widehat{O_{3}}=\left(\widehat{O_{1}}+\widehat{O_{2}}\right)+\widehat{O_{3}}$,
trong đó $\widehat{O_{1}}+\widehat{O_{2}}=\widehat{x^{\prime} O y}$.
b) Cho $\widehat{O_{1}}=60^{\circ}, \widehat{O_{3}}=70^{\circ}$. Tinh $\widehat{O_{2}}$.
Lời giải chi tiết:
a) Do $O x$ và $O x^{\prime}$ là hai tia đối nhau nên $\widehat{x O x^{\prime}}=180^{\circ}$.
Oy là tia nằm giữa hai tia $\mathrm{Ox}$ và $\mathrm{Ox}$ ‘ nên $\widehat{x^{\prime} O y}+\widehat{\mathrm{yOx}}=180^{\circ}$.
Khi đó $\widehat{x^{\prime} O_y}+\widehat{\mathrm{yOx}}=\left(\widehat{O_1}+\widehat{O_2}\right)+\widehat{O_3}=\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180^{\circ}$.
Vậy tổng ba góc $\mathrm{O}_1, \mathrm{O}_2, \mathrm{O}_3$ bằng $180^{\circ}$.
b) Ta có: $\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180^{\circ}$ nên $\widehat{O_2}=180^{\circ}-\widehat{O_1}-\widehat{O_3}=180^{\circ}-60^{\circ}-70^{\circ}=50^{\circ}$.
Vậy $\widehat{O_2}=50^{\circ}$.
a) Do $O x$ và $O x^{\prime}$ là hai tia đối nhau nên $\widehat{x O x^{\prime}}=180^{\circ}$.
Oy là tia nằm giữa hai tia $\mathrm{Ox}$ và $\mathrm{Ox}$ ‘ nên $\widehat{x^{\prime} O y}+\widehat{\mathrm{yOx}}=180^{\circ}$.
Khi đó $\widehat{x^{\prime} O_y}+\widehat{\mathrm{yOx}}=\left(\widehat{O_1}+\widehat{O_2}\right)+\widehat{O_3}=\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180^{\circ}$.
Vậy tổng ba góc $\mathrm{O}_1, \mathrm{O}_2, \mathrm{O}_3$ bằng $180^{\circ}$.
b) Ta có: $\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180^{\circ}$ nên $\widehat{O_2}=180^{\circ}-\widehat{O_1}-\widehat{O_3}=180^{\circ}-60^{\circ}-70^{\circ}=50^{\circ}$.
Vậy $\widehat{O_2}=50^{\circ}$.
Bài 3.36 trang 59 Toán 7 Toán 7 Kết nối tri thức tập 1
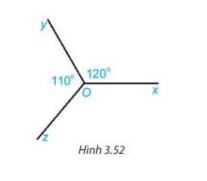
Cho Hình 3.52 , biết $\widehat{x O y}=120^{\circ}, \widehat{y O z}=110^{\circ}$.
Tính số đo góc zOx.
Gợi ý: Kẻ thêm tia đối của tia $O y$.
Tính số đo góc zOx.
Gợi ý: Kẻ thêm tia đối của tia $O y$.
Lời giải chi tiết:
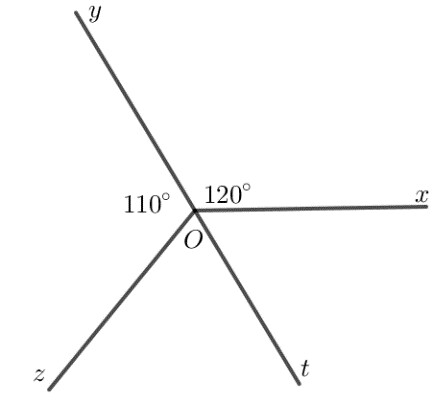
Kẻ $Ot$ là tia đối của tia $Oy$.
Do $Ot$ là tia đối của $Oy$ nên $\widehat{t O y}=180^{\circ}$.
hay $\widehat{y \mathrm{O} z}+\widehat{z O t}=180^{\circ}$.
Do đó $\widehat{z O t}=180^{\circ}-\widehat{y O} z=180^{\circ}-110^{\circ}=70^{\circ}$.
Có $\widehat{t O y}=180^{\circ}$ hay $\widehat{y \mathrm{Ox}}+\widehat{x O t}=180^{\circ}$.
Do đó $\widehat{x O t}=180^{\circ}-\widehat{y \mathrm{Ox}}=180^{\circ}-120^{\circ}=60^{\circ}$.
Do đó $\widehat{x O z}=\widehat{z O t}+\widehat{x O t}=70^{\circ}+60^{\circ}=130^{\circ}$.
Vậy $\widehat{x O z}=130^{\circ}$.

Kẻ $Ot$ là tia đối của tia $Oy$.
Do $Ot$ là tia đối của $Oy$ nên $\widehat{t O y}=180^{\circ}$.
hay $\widehat{y \mathrm{O} z}+\widehat{z O t}=180^{\circ}$.
Do đó $\widehat{z O t}=180^{\circ}-\widehat{y O} z=180^{\circ}-110^{\circ}=70^{\circ}$.
Có $\widehat{t O y}=180^{\circ}$ hay $\widehat{y \mathrm{Ox}}+\widehat{x O t}=180^{\circ}$.
Do đó $\widehat{x O t}=180^{\circ}-\widehat{y \mathrm{Ox}}=180^{\circ}-120^{\circ}=60^{\circ}$.
Do đó $\widehat{x O z}=\widehat{z O t}+\widehat{x O t}=70^{\circ}+60^{\circ}=130^{\circ}$.
Vậy $\widehat{x O z}=130^{\circ}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài tập cuối chương 3 trang 59 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





