Giải SGK bài 8 trang 30 Toán 6 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các hoạt động, vận dụng, luyện tập cũng như bài tập trong bài Quan hệ chia hết và tính chất. Đây là bài học thuộc Bài 8 chương 2 SGK Toán 6 Kết nối tri thức tập 1 trang 30, 31, 32, 33. Mong rằng các bạn đã cố gắng thử sức với những bài tập này trước khi xem lời giải của HocThatGioi và có một buổi học thật vui vẻ!
Trả lời câu hỏi SGK trang 30, 31, 32 Toán 6 Kết nối tri thức tập 1
Cùng HocThatGioi đi tìm đáp án cho các hoạt động, luyện tập và vận dụng ở các trang 30, 31, 32 SGK Toán 6 Kết nối tri thức tập 1 trong bài Quan hệ chia hết và tính chất ở ngay bên dưới nhé!
Câu hỏi 1 trang 30
$24$ ? $6$
$45$ ? $10$
$35$ ? $5$
$42$ ? $4$
+) Số $24$ chia hết cho $6$ vì $24 : 6 = 4$ và không có dư nên $24 \vdots 6$
+) Số $45$ không chia hết cho $10$ vì $45$ chia $10$ bằng $4$ và dư $5$ nên $45 \not \vdots 10$
+) Số $35$ chia hết cho $5$ vì $35 : 5 = 7$ và không có dư nên $35 \not \vdots 5$
+) Số $42$ không chia hết cho $4$ vì $42$ chia $4$ bằng $10$ và dư $2$ nên $42 \not \vdots 4$.
Câu hỏi 2 trang 30

Ta có:
$15 : 5 = 3$ và không có dư nên $15 \vdots 3$
$15 : 6 = 2$ và dư 3 nên $15 \not \vdots 6$
Do đó $5$ là ước của $15$ và $6$ không là ước của $15$.
Vậy bạn Vuông đúng.
Hoạt động 1 trang 31
Ta sẽ thực hiện phép chia $12$ cho các số từ $1$ đến $12$
Ta có bảng sau:
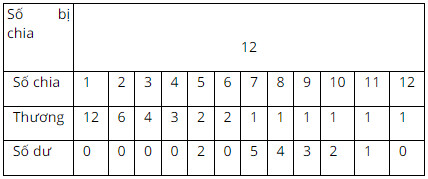
Qua bảng trên ta thấy: phép chia có số dư bằng $0$ là phép chia hết, do đó $12$ chia hết cho các số: $1; 2; 3; 4; 6; 12$
Hay $1; 2; 3; 4; 6; 12$ là các ước của $12$.
Vậy $Ư(12) = {1; 2; 3; 4; 6; 12}$
Hoạt động 2 trang 31
Ta sẽ thực hiện phép nhân $8$ với các số từ $0;1; 2; 3; 4$….
Ta có bảng sau:
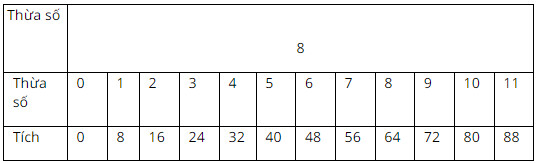
Từ bảng trên ta thấy các bội của $8$ nhỏ hơn $80$ là: $0; 8; 16; 24; 32; 40; 48; 56; 64; 72$
Nên ta viết: $B(8) = {0; 8; 16; 24; 32; 40; 48; 56; 64; 72}$
Luyện tập 1 trang 31
b) Hãy tìm tất cả các bội nhỏ hơn $50$ của $4$.
a) Lần lượt chia $20$ cho các số tự nhiên từ $1$ đến $20$, ta thấy $20$ chia hết cho $1; 2; 4; 5; 10; 20$ nên
$Ư(20) = {1; 2; 4; 5; 10; 20}.$
b) Lần lượt nhân $4$ với $0; 1; 2; 3; 4; 5;$ … ta được các bội của $4$ là: $0; 4; 8; 12; 16; 20; 24; 28; 32; 36; 40; 44; 48; 52;…$
Các bội của $4$ nhỏ hơn $50$ là: $B(4) = {0; 4; 8; 12; 16; 20; 24; 28; 32; 36; 40; 44; 48}$
Thử thách nhỏ trang 31
Ba ước khác nhau của $12$ có tổng là $12$ là: $2; 4; 6.$
Hoạt động 3 trang 31
Ta chọn hai số chia hết cho $5$ là: $10$ và $15$
Tổng của chúng là: $10 + 15 = 25$
Vì $25: 5 = 5$
Nên $25$ chia hết cho $5$ nên tổng $(10 + 15)$ chia hết cho $5.$
Hoạt động 4 trang 31
Ta chọn ba số chia hết cho $7$ là: $7; 14; 21$
Tổng của chúng là: $7 + 14 + 21 = 42$
Vì $42 : 7 = 6$
Nên $42$ chia hết cho $7$ nên tổng $(7 + 14 + 21)$ chia hết cho $7$.
Luyện tập 2 trang 32
a) $24 + 48$ có chia hết cho $4$ không. Vì sao?
b) $48 + 12 – 36$ có chia hết cho $6$ không. Vì sao?
a) Vì $24 ⋮ 4$ và $48 ⋮ 4$ nên theo tính chất chia hết của một tổng $(24 + 48) ⋮ 4$
b) Vì $48 ⋮ 6$; $12 ⋮ 6$ và $36 ⋮ 6$ nên $(48 + 12 – 36) ⋮ 6$
Vận dụng 1 trang 32
Vì $(21 + x) ⋮ 7$ mà $21⋮ 7$ nên theo tính chất chia hết của một tổng thì $x ⋮7$
Mà $x$ thuộc tập ${1; 14; 16; 22; 28}$ do đó $x = 14$ hoặc $x = 28$
Hoạt động 5 trang 32
Ta chọn hai số: $10$ chia hết cho $5$ và $6$ không chia hết cho $5$
Tổng của chúng là: $10 + 6 = 16$
Vì $16 : 5 = 3$ (dư $1$)
Do đó $16$ không chia hết cho $5$ nên tổng $(10 + 6)$ không chia hết cho $5$.
Hoạt động 6 trang 32
Ta chọn ba số trong đó hai số $4; 8$ chia hết cho $4$ và $5$ không chia hết cho $4$
Tổng của chúng là: $4 + 8 + 5 = 17$
Vì $17 : 4 = 4$ (dư $1$)
Do đó $17$ không chia hết cho $4$ nên tổng $(4 + 8 + 5)$ không chia hết cho $4.$
Luyện tập 3 trang 33
a) $20 + 81$ có chia hết cho $5$ không. Vì sao?
b) $34 + 28 – 12$ có chia hết cho $4$ không. Vì sao?
a) Vì $20 ⁝ 5$ và $81 ⁝ 5$ nên $(20 + 81 \not \vdots 5$
Vậy $20 + 81$ không chia hết cho $5$.
b) Vì $28 ⁝ 4, 12 ⁝ 4$ và $34 \not \vdots 4$ nên $(34 + 28 – 12) \not \vdots 4.$
Vậy $34 + 28 – 12$ không chia hết cho $4.$
Vận dụng 2 trang 33
Vì $20 ⁝ 5; 45⁝5$, để $(20 + 45 + x) \not \vdots 5$ thì $x \not \vdots 5$.
Mà x thuộc tập ${5; 25; 39; 54}$ do đó $x = 39$ hoặc $x = 54$
Vậy $x ∈ {39;54}.$
Tranh luận trang 33

Theo mình, hai số không chia hết cho $4$ thì tổng của chúng có thể chia hết cho $4$ hoặc không chia hết cho $4$.
Ví dụ:
$5$ và $7$ là hai số không chia hết cho $4$ nhưng $(5 + 7) = 12 ⁝ 4$
$5$ và $9$ là hai số không chia hết cho $4$ nhưng $(5 + 9) = 14 \not \vdots 4$
Vậy hai số không chia hết cho $4$ thì chưa kết luận được tổng có chia hết cho $4$ hay không.
Giải bài tập SGK trang 33 Toán 6 Kết nối tri thức tập 1
Những bài tập SGK ở cuối bài Quan hệ chia hết và tính chất trang 33 SGK Toán 6 Kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 2.1 trang 33
+) Lần lượt chia $30$ cho các số tự nhiên từ $1$ đến $30$, ta thấy $30$ chia hết cho $1; 2; 3; 5; 6; 10; 15; 30$ nên $Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.$
+) Lần lượt chia $35$ cho các số tự nhiên từ $1$ đến $35$, ta thấy $35$ chia hết cho $1; 5; 7; 35 $ nên
$Ư(35) = {1; 5; 7; 35}. $
+) Lần lượt chia $17$ cho các số tự nhiên từ $1$ đến $17$, ta thấy $17$ chia hết cho $1; 17$ nên
$Ư(17) = {1; 17}.$
Bài 2.2 trang 33
Vì $16 : 4 = 4$, $24 : 4 = 6$, $35 : 4 = 8$ (dư $3$)
Nên $16 ⁝ 4$; $24 ⁝ 4$;
Vậy các số là bội của $4$ là: $16; 24$.
Bài 2.3 trang 33
a) $x ∈ B(7)$ và $x 5$
a) Lần lượt nhân $7$ với$ 0; 1; 2; 3; 4; 5;$ … ta được các bội của $7$ là: $0; 7; 14; 21; 28; 35; 42; 49; 56; 63; 70;$…
Ta được $B(7) = {0; 7; 14; 21; 28; 35; 42; 49; 56; 63; 70;…}$
Mà $x ∈ B(7)$ và $x $ 5 nên $y ∈ {10; 25; 50}.$
Bài 2.4 trang 33
a) $15 + 1 975 + 2 019$;
b) $20 + 90 + 2 025 + 2 050$.
a) Vì $15 ⁝ 5; 1975 ⁝ 5$ nhưng $2019 \not \vdots 5$ nên $(15 + 1 975 + 2 019) \not \vdots 5$
Vậy tổng $15 + 1 975 + 2 019$ không chia hết cho $5$.
b) Vì $20 ⁝ 5; 90 ⁝ 5; 2025 ⁝ 5; 2050 ⁝ 5$ nên $(20 + 90 + 2 025 + 2 050) ⁝ 5$
Vậy tổng $20 + 90 + 2 025 + 2 050$ chia hết cho $5$.
Bài 2.5 trang 33
a) $100 – 40$
b) $80 – 16$
a) Vì $100 \not \vdots 8$ và $40 ⁝ 8$ nên $(100 – 40) \not \vdots 8$
Vậy hiệu $100 – 40$ không chia hết cho $8.$
b) Vì $8 ⁝ 8$ và $16 ⁝ 8$ nên theo tính chất chia hết của một hiệu thì $(80 – 16) ⁝ 8$
Vậy hiệu $80 – 16$ chia hết cho $8. $
Bài 2.6 trang 33
a) $219.7 + 8$ chia hết cho $7$;
b) $8.12 + 9$ chia hết cho $3$.
a) Vì $7 ⁝ 7$ nên $(219.7) ⁝ 7$ và $8 \not \vdots 7$ do đó $(219.7 + 8) \not \vdots 7$.
b) Vì $12 ⁝ 3$ nên $(8.12) ⁝ 3$ và $9 ⁝ 3$ do đó $(8.12 + 9) ⁝ 3$.
Vậy khẳng định b là đúng.
Bài 2.7 trang 33
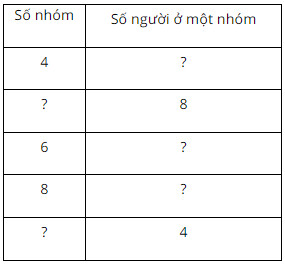
Ta thấy số học sinh bằng số nhóm nhân với số người ở một nhóm (Số người, số nhóm đều là số tự nhiên khác 0)
Do đó:
Số nhóm = Số học sinh : Số người ở một nhóm
Số người ở một nhóm = Số học sinh : Số nhóm
Ta có bảng sau:
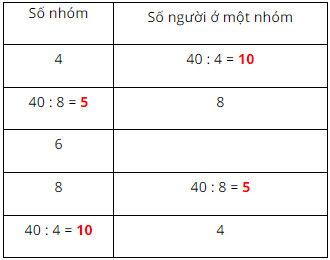
Bài 2.8 trang 33
Gọi số người mỗi nhóm được chia là$ x$ (người)
Ta có mỗi nhóm có ít nhất $2$ người và không quá $10$ người nên $\mathrm{x} \in \mathbb{N}^* ; 2 \leq \mathrm{x} \leq 10$
Vì đội thể thao của trường có $45$ vận động viên và huấn luyện viên chia thành các nhóm mà mỗi nhóm có số người như nhau nên $45 ⁝ x$ hay $x ∈ Ư(45)$
Ta lại có $Ư(45) = {1; 3; 5; 9; 15; 45}$
Mà $2 ≤ x ≤ 10$ do đó $x ∈ {3; 5; 9}$
Với số người mỗi nhóm được chia là $3$ người thì số nhóm là: $45 : 3 = 15$ (nhóm)
Với số người mỗi nhóm được chia là $5$ người thì số nhóm là: $45 : 5 = 9$ (nhóm)
Với số người mỗi nhóm được chia là $9$ người thì số nhóm là: $45 : 9 = 5$ (nhóm)
Vậy huấn luyện viên có thể chia thành $15$ nhóm, $9$ nhóm hoặc $5$ nhóm
Bài 2.9 trang 33
b) Tìm x thuộc tập ${22; 24; 45; 48}$ biết $60 + x$ không chia hết cho $6$
a) Vì $56 – x$ chia hết cho $8$ mà $56$ chia hết cho $8$ nên theo tính chất chia hết của một hiệu thì $x$ chia hết cho $8$
Mà x thuộc tập ${23; 24; 25; 26}$, trong các số đó, chỉ có số $24$ chia hết cho $8$ nên $x = 24$
Vậy $x ∈ 24$ .
b) Vì $60 + x$ không chia hết cho $6$ mà $60$ chia hết cho $6$ nên $x$ không chia hết cho $6$
Mà $x$ thuộc tập ${22; 24; 45; 48}$, trong các số đó thì có hai số $22$ và $45$ không chia hết cho $6$ nên $x = 22$ hoặc $x = 45$
Vậy $x ∈ { 22;45 }$.
Hi vọng các bạn có thể hiểu hết được những lời giải mà HocThatGioi trình bày ở trên trong bài Quan hệ chia hết và tính chất trang 30-33 SGK Toán 6 Kết nối tri thức tập 1 cũng như nắm vững được nội dung bài học. Chúc các bạn học tốt!





