Giải SGK bài Ước chung. Ước chung lớn nhất Toán 6 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các hoạt động, vận dụng, luyện tập cũng như bài tập trong bài Ước chung. Ước Chung lớn nhất. Đây là bài học thuộc SGK bài 11 trang 48, 49, 50, 51, 51 chương 2 Toán 6 Kết nối tri thức tập 1. Mong rằng các bạn đã cố gắng thử sức với những bài tập này trước khi xem lời giải của HocThatGioi và có một buổi học thật vui vẻ!
Giải câu hỏi mục 1 trang 48, 49 SGK Toán 6 Kết nối tri thức tập 1
Dưới đây là phương pháp và lời giải chi tiết cho các câu hỏi hoạt động thuộc mục 1 Ước chung. Ước chung lớn nhất ở trang 48, 49 bài 11 SGK Toán 6 Kết nối tri thức tập 1. Các bạn có thể tham khảo ngay đáp án bên dưới nhé!
Hoạt động 1 trang 48
Muốn tìm các ước của a (a > 1), ta lần lượt chia a cho các số tự nhiên từ 1 đến a để xem a chia hết cho số nào thì số đó là ước của a.
Ta thấy: 24 chia hết cho các số: 1; 2; 3; 4; 6; 8; 12; 24 nên $Ư(24)$ = {1; 2; 3; 4; 6; 8; 12; 24}
Ta thấy: 28 chia hết cho các số: 1; 2; 4; 7; 14; 28 nên $Ư(28)$ = {1; 2; 4; 7; 14; 28}
Hoạt động 2 trang 48
Tìm các số vừa là ước của 24, vừa là ước của 28.
Ta thấy các số vừa thuộc tập hợp $Ư(24)$, vừa thuộc tập hợp $Ư(28)$ là 1,2,4.
$ƯC(24, 28)$ = {1; 2; 4}
Hoạt động 3 trang 48
Tìm số lớn nhất trong các số vừa tìm được ở hoạt động 2.
Số lớn nhất trong $ƯC(24; 28)$ là 4
Câu hỏi trang 49
Tìm Ư(90) và Ư(10) => ƯC(90, 10)
$ƯCLN(90, 10)$ là số lớn nhất trong tập hợp $ƯC(90, 10)$
$Ư(90)$ = {1; 2; 3; 5; 9; 10; 18; 30; 45; 90}
$Ư(10)$ = {1; 2; 5; 10}
=> $ƯC(90, 10)$ = {1; 2; 5; 10}
=> $ƯCLN(90, 10)$ = 10
Luyện tập 1 trang 49
Xét xem 3 có thuộc ước chung của 12 và 15 hay không. Nếu có thì số bóng xanh và đỏ có thể chia đều được cho 3 người.
Ta có: $3$ ∈ $Ư(12)$ ; $3$ ∈ $Ư(15)$ nên $3$ ∈ $ƯC(12, 15)$
Do đó bố có thể chia số bóng cho ba anh em Việt, Hà và Nam đều như nhau.
Vận dụng 1 trang 49
a) Có thể chia được thành bao nhiêu nhóm học sinh?
b) Có thể chia nhiều nhất bao nhiêu nhóm học sinh?
Số nhóm có thể chia được là ước chung của 36 và 40.
Số nhóm có thể chia nhiều nhất là ƯCLN của 36 và 40.
a) Gọi x là số nhóm học sinh chia được ( x ∈ N* )
Khi đó x ∈ ƯC(36, 40)
$Ư(36)$ = {1; 2; 3; 4; 6; 9; 12; 18; 36}
$Ư(40)$ = {1; 2; 4; 5; 8; 10; 20; 40}
=> $x ∈ {1; 2; 4}$
Vậy có thể chia được thành 1; 2 hoặc 4 nhóm học sinh
b) Số nhóm chia được nhiều nhất là $ƯCLN(36, 40)$ = 4.
Giải câu hỏi mục 2 trang 49,50,51 SGK Toán 6 Kết nối tri thức tập 1
Tiếp theo sau đây là phần hướng dẫn cũng như lời giải chi tiết cho các hoạt động thuộc mục 2 Cách tìm ước chung lớn ở trang 49,50,51 bài 11 SGK Toán 6 Kết nối tri thức tập 1. Cùng HocThatGioi đi tìm đáp án của câu hỏi mục 2 này ngay nhé.
Câu hỏi 1 trang 50
– Chọn ra các thừa số nguyên tố chung. Sau đó ập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Các thừa số nguyên tố chung là 3 và 5. Số mũ nhỏ nhất của 3 là 1; của 5 là 1. Do đó $ƯCLN(45, 150) = 3.5 = 15$
Luyện tập 2 trang 50
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:
– Phân tích mỗi số ra thừa số nguyên tố
– Chọn ra các thừa số nguyên tố chung
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
$36 = 2^2.3^2$
$84 = 2^2.3.7$
Ta thấy 2 và 3 là các thừa số nguyên tố chung của 36 và 84. Số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1 nên
$ƯCLN(36, 84) = 22.3 = 12$
Vận dụng 2 trang 50
Số hàng dọc nhiều nhất có thể xếp được là ƯCLN(24, 28, 36).
Số hàng dọc nhiều nhất có thể xếp được là ƯCLN(24, 28, 36)
Ta có:
$24 = 2^3.3$
$28 = 2^2.7$
$36 = 2^2.3^2$
Ta thấy 2 là thừa số nguyên tố chung của 24; 28 và 36. Số mũ nhỏ nhất của 2 là 2 nên $ƯCLN( 24, 28, 36 )=2^2=4$
Vậy có thể xếp được nhiều nhất 4 hàng dọc.
Câu hỏi 2 trang 50
$ƯC(a,b)$ là ước của $ƯCLN (a,b)$
$ƯC(75, 105) = Ư(15) = {1; 3; 5; 15}$
Thử thách nhỏ trang 51
a) Hỏi số tiền để mua một vé (giá vé được tính theo đơn vị nghìn đồng) có thể là bao nhiêu, biết giá vé lớn hơn 2000 đồng?
b) Có bao nhiêu học sinh tham gia chuyến đi, biết số học sinh trong lớp trong khoảng từ 20 đến 40 người?
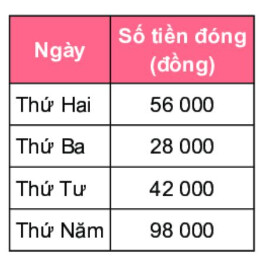
a) Giá tiền 1 vé là ƯC(56, 28,42, 98).
b) Số học sinh tham gia = Tổng số tiền thu được : giá tiền 1 vé
a) Gọi giá tiền 1 vé là $x$ (nghìn đồng; $x>2$).
Ta có $x ∈ ƯC(56, 28, 42, 98)$
Ta có: 56 = 23.7; 28 = 22.7; 42 = 2.3.7; 98 = 2.72
=> $ƯCLN(56, 28, 42, 98) = 2.7 =14$
=> $ƯC(56, 28, 42, 98) = Ư(14) = {1; 2; 7; 14}$
Mà $x>2$ nên $x ∈ {7; 14}$
Vậy giá tiền 1 vé có thể là 7 000 đồng hoặc 14 000 đồng.
b) Tổng số tiền cô Lan thu được là: 56 000 + 28 000 + 42 000 + 98 000 = 224 000 đồng
TH1:Giá vé là 7000 đồng thì số học sinh tham gia chuyến đi là: 224 000 : 7 000 = 32 học sinh (thỏa mãn).
TH2: Giá vé là 14000 đồng thì số học sinh tham gia chuyến đi là: 224 000 : 14 000 = 16 học sinh (loại).
Vậy số học sinh tham gia chuyến đi là 32 em.
Giải câu hỏi mục 3 trang 51,52 SGK Toán 6 Kết nối tri thức tập 1
Dưới đây là những phương pháp và lời giải chi tiết cho các hoạt động, luyện tập, câu hỏi thuộc mục 3 Phân số tối giản bài ở trang 51,52 SGK Toán 6 Kết nối tri thức tập 1. Các bạn hãy xem ngay cách giải dưới đây nhé!
Câu hỏi trang 51
Nếu tử và mẫu của phân số có ước chung lớn nhất là 1 thì phân số đã tối giản.
Để rút gọn 1 phân số về dạng tối giản, ta chia cả tử và mẫu của phân số cho ƯCLN của chúng
Phân số đã cho chưa tối giản vì ƯCLN(16,10) = 2
$\frac{16}{10}$ = $\frac{16:2}{10:2}$ = $\frac{8}{5}$
Luyện tập 3 trang 52
a) $\frac{90}{27}$ b) $\frac{50}{125}$
Chia cả tử và mẫu của phân số cần rút gọn cho ước chung lớn nhất của tử và mẫu.
a) Ta có: $90=2.3^2.5; 27=3^3$
Thừa số nguyên tố chung là 3 với số mũ nhỏ nhất là 2 nên $ƯCLN(90,27)=3^2=9$
$\frac{90}{27}$ = $\frac{90:9}{27:9}$ = $\frac{10}{3}$
b) Ta có: $50=2.5^; 125=5^3$
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 2 nên $ƯCLN(50,125)=5^2=25$
$\frac{50}{125}$ = $\frac{50:25}{125:25}$ = $\frac{2}{5}$
Giải bài tập SGK trang 52
Những bài tập SGK ở cuối bài Ước chung. Ước chung lớn nhất trang 52 SGK Toán 6 Kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 2.30 trang 52
a) 30 và 45 ;
b) 42 và 70 .
– Tìm tập hợp các ước của các số đã cho.
– Lấy các số chung trong các tập hợp vừa tìm được.
a) $Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}$
$Ư(45) = {1; 3; 5; 9; 15; 45}$
Vậy $ƯC(30, 45) = {1; 3; 5; 15}$
b) $Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}$
$Ư(70) = {1; 2; 5; 7; 10; 14; 35; 70}$
Vậy $ƯC(42, 70) = {1; 2; 7; 14}.$
Bài 2.31 trang 52
a) 40 và 70 ;
b) 55 và 77 .
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:
– Phân tích mỗi số ra thừa số nguyên tố
– Chọn ra các thừa số nguyên tố chung;
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
a) Ta có: $40 = 2^3.5$; $70 = 2.5.7$
Vậy $ƯCLN(40, 70) = 2.5 = 10$
b) Ta có: $55 = 5.11$; $77 = 7.11$
Vậy $ƯCLN(55, 77) = 11$
Bài 2.32 trang 52
a) $2^{2} \cdot 5$ và $2 \cdot 3 \cdot 5$;
b) $2^{4} \cdot 3 ; 2^{2} \cdot 3^{2} \cdot 5$ và $2^{4} \cdot 11$.
– Chọn ra các thừa số nguyên tố chung;
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
a) $2^2.5$ và $2.3.5$
Ta thấy 2 và 5 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 1 và số mũ nhỏ nhất của 5 là 1 nên ƯCLN cần tìm là $2.5 = 10$
b) $2^4.3; 2^2.3^2.5$ và $2^4.1^1$
Ta thấy 2 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 2 nên ƯCLN cần tìm là $2^2 = 4$
Bài 2.33 trang 52
a) Phân tích $a$ và $b$ ra thừa số nguyên tố;
b) Tìm ƯCLN( $a, b)$, rồi tìm ƯC $(a, b)$.
a) Phân tích mỗi số ra thừa số nguyên tố
b) Chọn ra các thừa số nguyên tố chung;
Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
=> Ước chung của hai hay nhiều số là ước của ước chung lớn nhất của hai hay nhiều số đó
a) $a = 72 = 2^3.3^2$
$b = 96 = 2^5.3$
b) Ta thấy 2 và 3 là các thừa số chung của 72 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên $ƯCLN(72, 96) = 23.3 = 24$
$ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.$
Bài 2.34 trang 52
a) $\frac{50}{85}$;
b) $\frac{23}{81}$.
Nếu tử và mẫu của phân số đã cho có ước chung lớn nhất khác 1 thì phân số chưa tối giản, nếu có ước chung lớn nhất bằng 1 thì phân số đã tối giản.
a) $\frac{50}{85}$
Ta có: $50=2.5^2; 85=5.17$
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5. Do đó, $\frac{50}{85}$ chưa là phân số tối giản
Ta có: $\frac{50}{85}$ = $\frac{50:5}{85:5}$ = $\frac{10}{17}$
b) $\frac{23}{81}$
Ta có: $23=23; 81=3^4$
Chúng không có thừa số nguyên tố chung nên $ƯCLN(23, 81) = 1$. Do đó, $\frac{23}{81}$ là phân số tối giản.
Bài 2.35 trang 52
Hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số:
4 và 9; 8 và 27
Chú ý: Ta có thể lấy các ví dụ khác
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 11 – Ước chung. Ước chung lớn nhất trang 48, 49, 50, 51, 51 Toán 6 Kết nối tri thức tập 1.. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





