Giải SGK Bài 10 Chương 3 Trang 51, 52, 53, 54 Toán 7 Kết Nối Tri Thức
Ở bài viết này, HocThatGioi sẽ cùng bạn giải quyết tất cả những câu hỏi khởi động, vận dụng, bài tập trong bài Tiên đề Euclid. Tính chất của hai đường thẳng song song Các bài tập sau đây thuộc bài 10 chương 3 – Góc và đường thẳng song song. Hy vọng, sau bài viết này các bạn có thể nắm rõ những kiến thức đã học và có thể áp dụng chúng một cách dễ dàng theo những lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi sách giáo khoa trang 51, 52 SGK Bài 10 Chương 3 Kết Nối Tri Thức
Dưới đây là phương pháp cụ thể và bài giải chi tiết, dễ hiểu cho các câu hỏi hoạt động, thực hành cùng phần luyện tập ở các trang 51, 52 trong bài Tiên đề Euclid. Tính chất của hai đường thẳng song song. Cùng HocThatGioi đi tìm đáp án và phương pháp giải hay nhất ngay nhé!
Hoạt động 1 SGK Trang 51
Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a.
Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a.
Em có nhận xét gì về vị trí của hai đường thẳng b và c?
Vẽ hình, nhận xét.
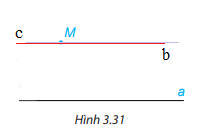
Luyện tập 1 trang 52
(1) Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.
(2) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.
(3) Qua điểm M nằm ngoài đường thẳng a, có ít nhất một đường thẳng song song với a.
Tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Phát biểu (1) là diễn đạt đúng nội dung của Tiên đề Euclid
Phát biểu (2) là sai vì có vô số đường thẳng song song với một đường thẳng cho trước
Phát biểu (3) là sai vì qua điểm M nằm ngoài đường thẳng a, có duy nhất một đường thẳng song song với a
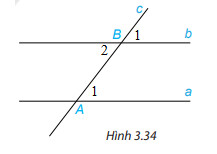
Hoạt động 2 SGK trang 52
a) Em hãy đo một cặp góc so le trong rồi rút ra nhận xét.
b) Em hãy đo một cặp góc đồng vị rồi rút ra nhận xét.
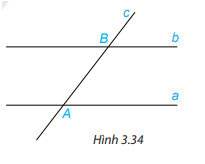
a) Chọn một cặp góc ở vị trí so le trong rồi đo góc.
b) Chọn một cặp góc ở vị trí đồng vị rồi đo góc.
b) Ta có: \widehat{B_{1}} và \widehat{A_{1}} là hai góc ở vị trí đồng vị. Đo góc ta được: \widehat{B_{1}} = \widehat{A_{1}}
Luyện tập 2 trang 53 SGK
Hãy tính số đo các góc $BMN$ và $ACB$.
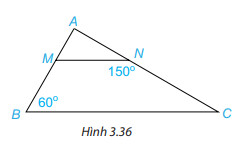
Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau
Hai góc đồng vị bằng nhau
1. Vì $MN//BC$ nên \widehat{AMN} = \widehat{ABC} (2 góc đồng vị), mà \widehat{ABC} = 60^{\circ} nên \widehat{AMN} = 60^{\circ}
Vì \widehat{AMN} + \widehat{BMN} = 180^{\circ} (2 góc kề bù)
\Longrightarrow 60^{\circ} + \widehat{BMN} = 180^{\circ}
\Longrightarrow \widehat{BMN} = 180^{\circ} – 60^{\circ} = 120^{\circ}
Vì \widehat{AMN} + \widehat{MNC} = 180^{\circ} ( 2 góc kể bù)
\Longrightarrow \widehat{ANM} + 150^{\circ} = 180^{\circ}
\Longrightarrow \widehat{ANM} = 180^{\circ} – 150^{\circ} = 130^{\circ}
Vì $MN//BC$ nên \widehat{ANM} = \widehat{ACB} (2 góc đồng vị), mà \widehat{ANM} = 30^{\circ} nên \widehat{ACB} = 30^{\circ}
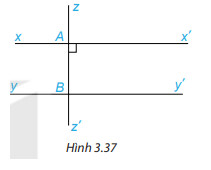
2. Vì xx’ // yy’ nên \widehat{x’AB} = \widehat{ABy} (2 góc so le trong)
Mà zz’⊥ xx’ nên \widehat{x’AB} = 90^{\circ}
Do đó, \widehat{ABy} = 90^{\circ} nên zz’ vuông góc với yy’.
Giải bài tập SGK trang 53, 54 Toán 7 Kết Nối Tri Thức
Những bài tập SGK ở cuối bài trang 53, 54 sách Toán 7 kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi hoàn thành tốt những bài toán này nhé!
Bài tập 3.17 SGK Toán 7 Bài 10
Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau
Hai góc đồng vị bằng nhau
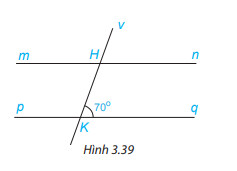
Vì mn//pq nên
+ \widehat{mHK} = \widehat{HKq} ( 2 góc so le trong), mà \widehat{HKq} = 70^{\circ} \Longrightarrow \widehat{mHK} = 70^{\circ}
+ \widehat{vHn} = \widehat{HKq} ( 2 góc góc đồng vị), mà \widehat{HKq} = 70^{\circ} \Longrightarrow \widehat{HKq} = 70^{\circ}
Giải bài 3.18 trang 53
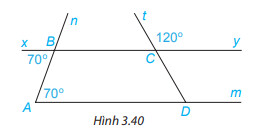
a) Giải thích tại sao $Am//By$.
b) Tính \widehat{CDm}
a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.
b) Sử dụng tính chất của 2 đường thẳng song song
a) Vì \widehat{xBA} = \widehat{BAD} (= 70^{\circ} ), mà 2 góc này ở vị trí so le trong nên $Am // By$ ( Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì $Am // By$ nên \widehat{CDm} = \widehat{tCY} ( 2 góc đồng vị), mà \widehat{tCy} = 120^{\circ} \Longrightarrow \widehat{CDm} = 120^{\circ} .
Giải bài 3.19 Trang 54
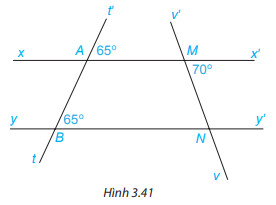
a) Giải thích tại sao xx’//yy’.
b) Tính số đo góc $MNB$.
a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.
b) Sử dụng tính chất của 2 đường thẳng song song
a) Vì \widehat{t’AM} =\widehat{ABN} (= 65^{\circ}, mà 2 góc này ở vị trí đồng vị nên xx’//yy’ ( Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì xx’//yy’ nên \widehat{x’MN} = \widehat{MNB} (2 góc so le trong), mà \widehat{x’MN} = 70^{\circ}
\Longrightarrow \widehat{MNB} = 70^{\circ}
Giải bài 3.20 trang 54
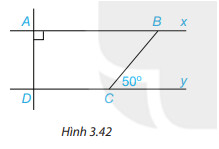
Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau
Hai góc đồng vị bằng nhau
Vì Ax // Dy, mà AD ⊥ Ax nên AD ⊥ Dy. Do đó, \widehat{ADC} = 90^{\circ} ;
Vì Ax // Dy nên \widehat{ABC} = \widehat{BCy} (2 góc so le trong), mà \widehat{BCy} = 50^{\circ} ; \Longrightarrow \widehat{ABC} = 50^{\circ} ; Vậy \widehat{ADC} = 90^{\circ} ; \widehat{ABC} = 50^{\circ} ;
Giải bày 3.21 trang 54
a) Ax’ // By b) By ⊥ HK
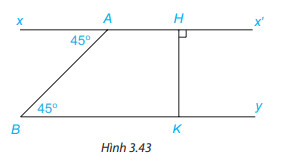
a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.
b) Sử dụng tính chất đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia
a) Vì \widehat{xAB} = \widehat{ABy} ( = 45^{\circ} )
Mà hai góc này ở vị trí so le trong
Do đó, xx’ // By ( Dấu hiệu nhận biết 2 đường thẳng song song) hay Ax’ // By
b) Cách 1:
Vì Ax' // By nên \widehat{x'HK} = \widehat{HKB} ( 2 góc so le trong)
Mà \widehat{x'HK} = 90^{\circ} nên \widehat{HKB} = 90^{\circ}
Do đó, Ax’ ⊥ HK
Cách 2:
Vì Ax’ // By, mà By ⊥ HK nên Ax’ ⊥ HK (đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia)
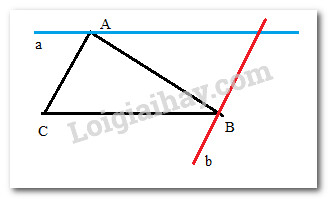
Giải bài 3.22 trang 54
Dựa vào tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
+) Qua điểm A nằm ngoài đường thẳng BC, chỉ có một đường thẳng song song với đường thẳng BC. Đường thẳng đó là a
+) Qua điểm B nằm ngoài đường thẳng AC, chỉ có một đường thẳng song song với đường thẳng BC. Đường thẳng đó là b
Như vậy, có thể vẽ được 1 đường thẳng a, 1 đường thẳng b.
Giải bài 3.23 trang 45
a) $MN//EF$
b) $HK//EF$
c) $HK//MN$
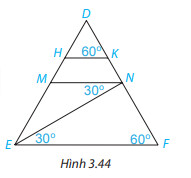
Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.
Sử dụng tính chất 2 đường thẳng cùng song song với 1 đường thẳng thứ ba thì chúng song song với nhau.
a) Vì \widehat{MNE} = \widehat{NEF} ( = 30^{\circ} ), mà 2 góc này ở vị trí so le trong nên MN//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì \widehat{DKH} = \widehat{DEF} ( = 60^{\circ} ), mà 2 góc này ở vị trí đồng vị nên HK//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)
c) Vì $MN//EF$; $HK//EF$ nên $HK//MN$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài 10 Chương 3 trang 51, 52, 53, 54 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





