Giải SGK bài 12 Bội chung, bội chung nhỏ nhất Toán 6 KNTT tập 1
Bài viết dưới đây tổng hợp các phương pháp và lời giải chi tiết về các hoạt động, câu hỏi, vận dụng, luyện tập, thử thách nhỏ và bài tập thuộc bài 12 Bội chung, bội chung nhỏ nhất nằm ở các trang 53, 54, 55, 56, 57 SGK Toán 6 Kết nối tri thức tập 1. Hy vọng các phương pháp và lời giải sau đây của HocThatGioi sẽ giúp bạn nắm rõ được bài học, tiếp thu thêm kiến thức để làm tốt các bài tương tự sau này. Cùng theo dõi ngay nhé!
Giải SGK câu hỏi mục 1 trang 53, 54 Toán 6 KNTT tập 1
Dưới đây sẽ tổng hợp những phương pháp, lời giải chi tiết cho các câu hỏi hoạt động, câu hỏi, luyện tập cùng vận dụng thuộc mục 1 Bội chung và bội chung nhỏ nhất nằm ở các trang 53, 54 bài 12 Toán 6 KNTT tập 1. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 53
Muốn tìm bội của một số tự nhiên $a$, ta lấy $a$ nhân lần lượt với các số 0; 1; 2; 3;…
B(6) = {0; 6; 12; 18; 24; 30; 36; 42, 48; 54,…}
B(9) = {0; 9; 18; 27; 36; 45; 54; 63,…}
Hoạt động 2 trang 53
Lấy các phần tử chung của hai tập hợp của hai tập hợp tìm được ở hoạt động 1.
$\mathrm{BC}(6, 9)=\{0 ; 18 ; 36 ; 54 ; \ldots\}$
Hoạt động 3 trang 53
Quan sát tập $\mathrm{BC}(6,9)$ vừa tìm được ở hoạt động 2 suy ra số cần tìm.
Số nhỏ nhất khác 0 trong tập $\mathrm{BC}(6,9)$ là 18.
Câu hỏi 1 trang 54
Nếu a ⋮ b thì BCNN(a, b) = a.
Do 36 ⋮ 9 nên BCNN(36,9) = 36
Vận dụng trang 54
Số tháng cần tìm là BCNN(6; 9).
Số tháng cần tìm là BCNN(6; 9)
B(6) = {0; 6; 12; 18; 24; 30; 36; 42, 48; 54, …}
B(9) = {0; 9; 18; 27; 36; 45; 54; 63, …}
Nên BC(6; 9) = {0; 18; 36; 54, …}
Do đó BCNN(6; 9) = 18
Vậy sau ít nhất 18 tháng nữa thì hai máy được bảo dưỡng cùng một tháng.
Giải SGK câu hỏi mục 2 trang 55, 56 Toán 6 KNTT tập 1
Dưới đây là những phương pháp, lời giải chi tiết cho các câu hỏi, luyện tập cùng thử thách nhỏ thuộc mục 2 Cách tìm bội chung nhỏ nhất nằm ở các trang 55, 56 bài 12 Toán 6 KNTT tập 1. Cùng xem đáp án ngay nhé!
Câu hỏi 2 trang 55
Chọn ra các thừa số nguyên tố chung và riêng.Sau đó, lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
Ta có: $9 = 3^2; 15 = 3 \cdot 5$
Thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 5. Số mũ lớn nhất của 3 là 2, của 5 là 1 nên
BCNN $(9, 15) = 3^2 \cdot 5= 45$
Câu hỏi 3 trang 55
Các bội chung là bội của bội chung nhỏ nhất.
BC(8, 6) = B(24) ={0; 24; 48; 72; 96; 120;…}
Vậy các bội chung nhỏ hơn 100 của 8 và 6 là : 0; 24; 48; 72; 96.
Luyện tập 2 trang 56
Phân tích mỗi số ra thừa số nguyên tố;
Chọn ra các thừa số nguyên tố chung và riêng;
Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
Phân tích 15 và 54 ra thừa số nguyên tố: $15 = 3 \cdot 5 ; 54 = 2 \cdot 33$
Ta thấy thừa số nguyên tố chung là $3$ và thừa số nguyên tố riêng là $2$ và $5$. Số mũ lớn nhất của $3$ là $3$, của $2$ là $1$, của $5$ là $1$ nên $BCNN (15, 54) = 2 \cdot 33 \cdot 5 = 270$
Do đó $BC(15, 54) = {0; 270; 540; 810; 1080; …}$
Vậy bội chung nhỏ hơn $1000$ của $15$ và $54$ là: $0; 270; 540; 810$.
Thử thách nhỏ trang 56
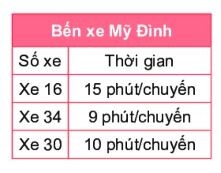
– Tính khoảng thời gian các xe cùng xuất bên so với lúc 10h35p (thời điểm đầu tiên xuất bến).
– Lấy 10h35p cộng lần lượt với khoảng thời gian tìm được.
Ta có 22h – 10h35p =11h25p = 685 phút
Thời gian các xe cùng xuất bến cách 10h35p các khoảng thời gian là BC(9, 10, 15) và nhỏ hơn 685 phút
Ta có: 9 = 32, 10 = 2 $\cdot$ 5, 15 = 3 $\cdot$ 5.
=> BCNN(9, 10, 15) = 2 $\cdot$ 32$\cdot$ 5 = 90
Như vậy, cứ sau 90 phút thì các xe lại cùng xuất phát
Các BC(9, 10, 15) và nhỏ hơn 685 là: 0; 90; 180; 270; 360; 450; 540; 630.
Ta lấy 10h35p cộng lần lượt với 0; 90; 180; 270; 360; 450; 540; 630 phút ta được:
Thời gian các xe cùng xuất bến là: 10h35p, 12h05p; 13h35p; 15h05p; 16h35p; 18h05p; 19h35p; 21h05p.
Giải SGK câu hỏi mục 3 trang 56, 57 Toán 6 KNTT tập 1
Dưới đây là các phương pháp, lời giải chi tiết cho các câu hỏi và luyện tập thuộc mục 3 Quy đồng mẫu các phân số nằm ở các trang 56, 57 bài 12 Toán 6 KNTT tập 1. Các bạn có thể tham khảo đáp án ngay bên dưới nhé.
Câu hỏi 4 trang 56
Để quy đồng mẫu hai phân số $\frac{a}{b}$ và $\frac{c}{d}$, ta phải tìm mẫu chung của hai phân số đó.
Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
Ta có: $9 = 3^2; 15= 3 \cdot 5$
Thừa số nguyên tố chung là 3, thừa số nguyên tố riêng là 5. Số mũ lớn nhất của 3 là 2, của 5 là 1
\Longrightarrow $BCNN 99, 15) = 3^2 \cdot 5 = 45$ nên ta chọn mẫu số chung là 45
$\frac{7}{9}$ $=$ $\frac{7 \cdot 5}{9 \cdot 5}$ $=$ $\frac{35}{45}$
$\frac{4}{15}$ $=$ $\frac{4 \cdot 3}{15 \cdot 3}$ $=$ $\frac{12}{45}$
Luyện tập 3 trang 57
a) $\frac{5}{12}$ và $\frac{7}{15}$
b) $\frac{2}{7}, \frac{4}{9}$ và $\frac{7}{12}$.
2. Thực hiện các phép tính sau:
a) $\frac{3}{8}+\frac{5}{24}$
b) $\frac{7}{16}-\frac{5}{12}$.
– Để quy đồng mẫu hai phân số $\frac{a}{b}$ và $\frac{c}{d}$, ta phải tìm mẫu chung của hai phân số đó.
Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
– Để cộng, trừ các phân số khác mẫu ta đi quy đồng mẫu số các phân số rồi thực hiện cộng(trừ) tử số và giữ nguyên mẫu.
1. a) Ta có $BCNN(12, 15) = 60$ nên ta lấy mẫu chung của hai phân số là $60$.
Thừa số phụ:
$60 : 12 =5; 60 : 15 = 4$
Ta được:
$\frac{5}{12}$ $=$ $\frac{5 \cdot 5}{12 \cdot 5}$ $=$ $\frac{25}{60}$
$\frac{7}{15}$ $=$ $\frac{7 \cdot 4}{15 \cdot 4}$ $=$$\frac{28}{60}$
b) Ta có $BCNN (7, 9, 12) = 252$ nên ta lấy mẫu chung của ba phân số là $252$.
Thừa số phụ:
$252:7 = 36; 252:9 = 28; 252:12 =21$
Ta được:
$\frac{2}{7}$ $=$ $\frac{2 \cdot 36}{7 \cdot 36}$ $=$ $\frac{72}{252}$
$\frac{4}{9}$ $=$ $\frac{4 \cdot 28}{7 \cdot 28}$ $=$ $\frac{112}{252}$
$\frac{7}{12}$ $=$ $\frac{7 \cdot 21}{12 \cdot 21}$ $=$ $\frac{147}{252}$
2. a) Ta có $BCNN (8, 24) = 24$ nên:
$\frac{3}{8}+\frac{5}{24}$ $=$ $\frac{3 \cdot 3}{8 \cdot 3}+\frac{5}{24}$ $=$ $\frac{9}{24}+\frac{5}{24}$ $=$ $\frac{14}{24}$ $=$ $\frac{7}{12}$
b) Ta có $BCNN (12, 16) = 48$ nên:
$\frac{7}{16}-\frac{5}{12}$ $=$ $\frac{7 \cdot 3}{16 \cdot 3}-\frac{5 \cdot 4}{12 \cdot 4}$ $=$ $\frac{21}{48}-\frac{20}{48}$ $=$$\frac{1}{48}$
Giải SGK bài tập trang 57 Toán 6 KNTT tập 1
Phần cuối cùng là các phương pháp và lời giải chi tiết của các bài tập nằm ở các trang 57 bài 12 Toán 6 Kết nối tri thức tập 1. Các bài tập này sẽ giúp bạn củng cố lại hệ thống kiến thức mình đã học. Các bạn có thể tham khảo hướng dẫn giải bên dưới nhé!
Bài 2.36 trang 57
a) 5 và 7 ;
b) 3,4 và 10 .
Tìm BCNN của các số
– Phân tích mỗi số ra thừa số nguyên tố
– Chọn ra các thừa số nguyên tố chung và riêng
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
Bội của BCNN là bội chung
a) Do 5 và 7 là hai số nguyên tố cùng nhau nên:
BCNN(5, 7) = 5.7 = 35 \Longrightarrow BC(5, 7) = B(35) = {0; 35; 70; 105; 140; 175; 210; …}
Vậy bội chung nhỏ hơn 200 của 5 và 7 là 0; 35; 70; 105; 140; 175.
b) Ta có: 3 = 3; 4 = 22; 10 = 2 $\cdot$ 5
Không có thừa số nguyên tố chung ; thừa số nguyên tố riêng là 2,3,5. Số mũ lớn nhất của 2;3;5 lần lượt là 2;1;1 nên BCNN(3, 4, 10) = 22 $\cdot$ 3 $\cdot$ 5 = 60
\Longrightarrow BC(3, 4, 10) = B(60) = {0; 60; 120; 180; 240; …}
Vậy bội chung nhỏ hơn 200 của 3, 4 và 10 là 0; 60; 120; 180.
Bài 2.37 trang 57
a) $2 \cdot 3^{3}$ và $3 \cdot 5$;
b) $2 \cdot 5 \cdot 7^{2}$ và $3 \cdot 5^{2} \cdot 7$.
– Chọn ra các thừa số nguyên tố chung và riêng
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
a) $2 \cdot 3^{3}$ và $3 \cdot 5$
Ta thấy các thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 2 và 5. Số mũ lớn nhất của 3 là 3; của 2 là 1; của 5 là 1.
Vậy BCNN cần tìm là 2 $\cdot$ 33 $\cdot$ 5 = 270
b) $2 \cdot 5 \cdot 7^{2}$ và $3 \cdot 5^{2} \cdot 7$
Ta thấy các thừa số nguyên tố chung là 5 và 7; thừa số nguyên tố riêng là 2 và 3. Số mũ lớn nhất của 5 là 2; của 7 là 2; của 2 là 1, của 3 là 1.
Vậy BCNN cần tìm là 2 $\cdot$ 3 $\cdot$ 52 $\cdot$ 72 = 7350.
Bài 2.38 trang 57
a) 30 và 45 ;
b) 18,27 và 45 .
– Phân tích mỗi số ra thừa số nguyên tố;
– Chọn ra các thừa số nguyên tố chung và riêng;
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
a) 30 và 45
30 = 2 $\cdot$ 3 $\cdot$ 5; 45 = 32 $\cdot$ 5
Ta thấy thừa số nguyên tố chung là 3 và 5; thừa số nguyên tố riêng là 2
Số mũ cao nhất của 3 là 2; số mũ cao nhất của 5 là 1; số mũ cao nhất của 2 là 1
Vậy BCNN(30, 45) = 2 $\cdot$ 32 $\cdot$ 5 = 90
b) 18, 27 và 45
18 = 2 $\cdot$ 32 ; 27 = 33 ; 45 = 32 $\cdot$ 5
Ta thấy thừa số nguyên tố chung là 3; thừa số nguyên tố riêng là 2 và 5
Số mũ cao nhất của 3 là 3; số mũ cao nhất của 2 là 1; số mũ cao nhất của 5 là 1
Vậy BCNN(18, 27, 45) = 2 $\cdot$ 33 $\cdot$ 5 = 270.
Bài 2.39 trang 57
a = BCNN(28, 32)
Cách tìm BCNN của các số
– Phân tích các số ra thừa số nguyên tố
– Chọn ra các thừa số nguyên tố chung và riêng;
– Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
Số tự nhiên a nhỏ nhất khác 0 và a ⋮ 28 và a ⋮ 32
Do đó a = BCNN(28, 32)
28 = 22 $\cdot$ 7
32 = 25
Thừa số nguyên tố chung là 2, thừa số nguyên tố riêng là 7. Số mũ lớn nhất của 2 là 5, của 7 là 1
Nên a = BCNN(28, 32) = 25 $\cdot$ 7 = 224.
Bài 2.40 trang 57
Số học sinh của lớp 6A là BC(3, 4, 9) và trong khoảng từ 30 đến 40.
Học sinh lớp 6A khi xếp thành 3 hàng, 4 hàng hay 9 hàng đều vừa đủ.
Nên số học sinh của lớp 6A là BC(3, 4, 9)
Ta có BCNN(3, 4, 9) = 36
Do đó BC(3, 4, 9) = {0; 36; 72; …}
Mà số học sinh lớp 6A từ 30 đến 40 nên số học sinh lớp 6A là 36.
Bài 2.41 trang 57
Số cây mỗi đội trồng được là BC(8, 11) và trong khoảng từ 100 đến 200.
Vì số cây hai đội trồng được như nhau mà mỗi công nhân đội I đã trồng 8 cây, mỗi công nhân đội II đã trồng 11 cây.
Nên số cây mỗi đội trồng được là BC(8, 11)
BCNN(8, 11) = 88
Do đó số cây mỗi đội trồng là BC(8, 11) = B(88) = {0; 88; 176; 264; …}
Mà số cây trong khoảng từ 100 đến 200 nên số cây mỗi đội trồng được là 176 cây.
Bài 2.42 trang 57
Số ngày ít nhất mà cún vừa được đi dạo, vừa được tắm là BCNN(2, 7)
Số ngày ít nhất mà cún vừa được đi dạo, vừa được tắm là BCNN (2, 7)
Mà 2 và 7 là hai số nguyên tố cùng nhau nên BCNN (2, 7) = 2 $\cdot$ 7 = 14
Vậy số ít nhất mà cún vừa được đi dạo, vừa được tắm là 14 ngày.
Bài 2.43 trang 57
a) $\frac{9}{12}$ và $\frac{7}{15}$;
b) $\frac{7}{10}, \frac{3}{4}$ và $\frac{9}{14}$.
Để quy đồng mẫu hai phân số $\frac{a}{b}$ và $\frac{c}{d}$, ta phải tìm mẫu chung của hai phân số đó.
Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
a) Ta có: $12 = 2^3 \cdot 3; 15 = 3 \cdot 5$
$BCNN (12, 15) = 2^3 \cdot 3 \cdot 5 = 60$ nên ta chọn mẫu chung là 60
$\frac{9}{12}$ $=$ $\frac{9 \cdot 5}{12 \cdot 5}$ $=$ $\frac{45}{60}$
$\frac{7}{15}$ $=$ $\frac{7 \cdot 4}{15 \cdot 4}$ $=$ $\frac{28}{60}$
b) Ta có: $10 = 2 \cdot 5; 4 = ^2; 14 = 2 \cdot 7$
$BCNN(10, 4, 14) = 2^2 \cdot 5 \cdot 7 =140$ nên ta chọn mẫu chung là 140.
$\frac{7}{10}$ $=$ $\frac{7 \cdot 14}{10 \cdot 14}$ $=$ $\frac{98}{140}$
$\frac{3}{4}$ $=$ $\frac{3 \cdot 35}{4 \cdot 35}$ $=$ $\frac{105}{140}$
$\frac{9}{14}$ $=$ $\frac{9 \cdot 10}{14 \cdot 10}$ $=$ $\frac{90}{140}$
Bài 2.44 trang 57
a) $\frac{7}{11}+\frac{5}{7}$;
b) $\frac{7}{20}-\frac{2}{15}$.
Để cộng, trừ các phân số khác mẫu ta đi quy đồng mẫu số các phân số rồi thực hiện cộng (trừ) tử số và giữ nguyên mẫu.
a) Mẫu số chung $= BCNN(11, 7) = 77$
Thừa số phụ: $77:11 = 7; 77:7 =11$.
Ta có:
$\frac{7}{11}+\frac{5}{7}$ $=$ $\frac{7 \cdot 7}{11 \cdot 7}+\frac{5 \cdot 11}{7 \cdot 11}$ $=$ $\frac{49}{77}+\frac{55}{77}$ $=$ $\frac{104}{77}$
b) Mẫu số chung $= BCNN (20, 15) = 60$
Thừa số phụ: $60:20 = 3; 60:15 =4$
Ta có:
$\frac{7}{20}-\frac{2}{15}$ $=$ $\frac{7 \cdot 3}{20 \cdot 3}-\frac{2 \cdot 4}{15 \cdot 4}$ $=$ $\frac{21}{60}-\frac{8}{60}$ $=$ $\frac{13}{60}$
Bài học hôm nay đến đây là kết thúc. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 12 trang 53, 54, 55, 56, 57 Toán 6 Kết nối tri thức Tập 1. Hy vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt. Hẹn gặp lại các bạn ở những bài học sau nhé!





