Giải SGK bài 14 Phép cộng và phép trừ số nguyên Toán 6 Kết nối tri thức tập 1
Bài viết sau sẽ đưa ra các phương pháp cũng như lời giải chi tiết nhất của toàn bộ các câu hỏi Luyện tập, khởi động, tranh luận và bài tập trong bài 14 Phép cộng và phép trừ số nguyên. Các câu hỏi bài tập này nằm ở các trang 67, 68, 69, 70, 71 SGK Toán 6 Kết nối tri thức tập 1. Hy vọng bài viết của HocThatGioi giúp bạn hiểu và nắm được các phương pháp làm bài một cách hiệu quả nhất.
Giải SGK câu hỏi mục 1 trang 67, 68 Toán 6 Kết nối tri thức tập 1
Dưới đây là phương pháp là lời giải chi tiết của các hoạt động luyện tập và vận dụng ở mục 1 Cộng hai số nguyên cùng dấu trang 67, 68 SGK Toán 6 Kết nối tri thức trong bài Phép cộng và phép trừ số nguyên mà bạn có thể tham khảo. Các bạn hãy theo dõi ngay nhé!
Hoạt động 1 trang 67
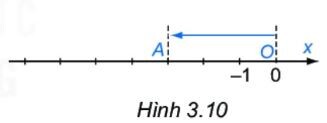
Trên trục số, chiều từ phải sang trái là chiều âm
Điểm $A$ biểu diễn số $-3$
Hoạt động 2 trang 67
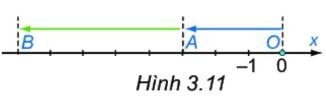
Trên trục số, chiều từ phải sang trái là chiều âm.
Vì từ điểm $A$ (điểm biểu diễn số $-3$) di chuyển sang trái 5 đơn vị, ta được điểm $B$. Vậy điểm $B$ biểu diễn số $-8$.
Mà $B$ chính là điểm biểu diễn kết quả của phép cộng $(-3)+(-5)$ nên $(-3)+(-5)=-8$
Luyện tập 1 trang 67
$(-12)+(-48)$;
$(-236)+(-1025)$.
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “$-$” trước kết quả.
$(-12) + (-48) = -(12 + 48) = -60$
$(-236) + (-1 025) = -(236 + 1 025) = -1 261$
Vận dụng 1 trang 68
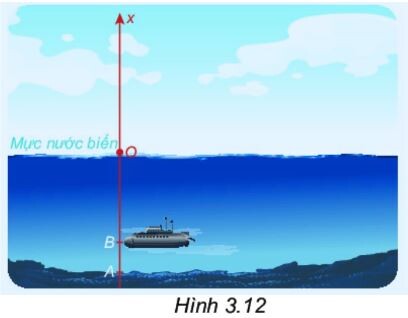
Một chiếc tàu ngầm cần lặn (coi là theo phương thẳng đứng) xuống điểm $A$ dưới đáy biển. Khi tàu đến điểm $B$ ở độ cao $-135 \mathrm{~m}$, máy đo báo rằng tàu còn cách $A$ một khoảng $45 \mathrm{~m}$. Hỏi điểm $A$ nằm ở độ cao bao nhiêu mét?
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “$-$” trước kết quả.
Vì tàu đến độ cao $-135 \mathrm{~m}$, còn phải lặn sâu thêm $45 \mathrm{~m}$ nữa (tức là đi thêm $-45 \mathrm{~m}$ nữa) nên điểm $A$ nằm ở độ cao: $(-135) + (-45) = -(135 + 45) = -180(\mathrm{m})$
Giải SGK câu hỏi mục 2 trang 68, 69 Toán 6 Kết nối tri thức tập 1
Tiếp đến là những câu hỏi mục 2 Cộng hai số nguyên khác dấu ở trang 68, 69 Toán 6 KNTT tập 1. Các bạn có thể tham khảo thêm về phương pháp cũng như lời giải chi tiết cho các hoạt động, luyện tập, vận dụng và tranh luận ở bên dưới.
Câu hỏi trang 68
Trên trục số hai điểm có cùng khoảng cách đến gốc $O$ được gọi là hai số đối nhau.
Số đối của $4, -5, 9, -11$ lần lượt là: $-4, 5, -9, 11$
Luyện tập 2 trang 68
Trên trục số hai điểm có cùng khoảng cách đến gốc $O$ được gọi là hai số đối nhau.

Hoạt động 3 trang 68
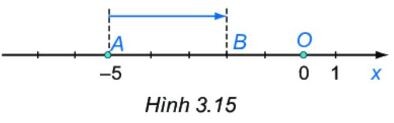
Di chuyển điểm $A$ (biểu diễn số $a$) sang phải $b$ đơn vị thì được điểm $B$ biểu diễn kết quả của phép cộng $a + b$
Điểm $B$ biểu diễn kết quả phép cộng: $(-5) + 3$.
Hoạt động 4 trang 68
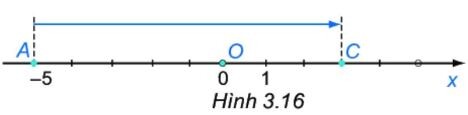
Di chuyển điểm $A$ (biểu diễn số $a$) sang phải $c$ đơn vị thì được điểm $C$ biểu diễn kết quả của phép cộng $a + c$
Điểm $C$ biểu diễn kết quả phép cộng: $(-5) + 8$
Luyện tập 3 trang 69
a) $203+(-195) ; \quad$
b) $(-137)+86$.
Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
a) $203 + (-195) = 203 – 195 = 8$
b) $(-137) + 86 = -(137 – 86) = -51$
Vận dụng 2 trang 69
Một máy thăm dò đáy biển ngày hôm trước hoạt động ở độ cao $-946 \mathrm{~m}$. Ngày hôm sau người ta cho máy nổi lên $55 \mathrm{~m}$ so với hôm trước. Hỏi ngày hôm sau máy thăm dò đáy biển hoạt động ở độ cao nào?
Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
Máy nổi lên $55 \mathrm{~m}$, tức là đi độ cao tăng thêm $+ 55 \mathrm{~m}$
Ngày hôm sau, máy thăm dò hoạt động ở độ cao:
$-946 + 55 = -(946 – 55) = -891 ( \mathrm{m})$
Tranh luận trang 69
Em hãy trả lời giúp Vuông.
Dựa vào quy tắc cộng hai số nguyên khác dấu:
Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
Tổng của hai số nguyên khác dấu (không đối nhau) mang dấu của số hạng có phần số tự nhiên lớn hơn. Tổng 2 số nguyên đối nhau là 0.
Do đó tùy trường hợp mà tổng của hai số nguyên khác dấu là số dương hoặc số âm hoặc bằng 0.
Giải SGK câu hỏi mục 3 trang 69, 70 Toán 6 Kết nối tri thức tập 1
Phần tiếp theo chính là phương pháp và lời giải chi tiết cho các câu hỏi hoạt động và luyện tập của mục 3 Tính chất của phép cộng ở trang 69, 70 Toán 6 KNTT. Các bạn có thể tham khảo để hiểu chi tiết ngay dưới đây nhé!
Hoạt động 5 trang 69
Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
$a + b = -7 + 11 = 11 – 7 = 4$
$b + a = 11 + (-7) = 11 – 7= 4$
Vậy $a + b = b + a$.
Hoạt động 6 trang 69
Thực hiện phép tính ở trong ngoặc trước.
$(a + b) + c = [2 + (-4)] + (-6) = [ -(4 – 2)] + (-6) = (-2) + (-6) = – (2 + 6) = -8$
$a + (b + c) = 2 + [(-4) + (-6)] = 2 + [ -(4 + 6)] = 2 + (-10) = – (10 – 2)= -8$
Vậy $(a + b) + c = a + (b + c)$
Luyện tập 4 trang 70
a) $(-2019)+(-550)+(-451)$;
b) $(-2)+5+(-6)+9$.
Áp dụng tính chất giao hoán và kết hợp của phép cộng để tính hợp lí
a) $(-2 019) + (-550) + (-451) = [(-2 019) + (-451)] + (-550) = (-2 470) + (-550) = -(2 470 + 550) = -3 020$
b) $(-2) + 5 + (-6) + 9 = [(-2) + 5 ]+[ (-6) + 9] = 3 + 3 = 6$
Giải SGK mục 4 trang 70, 71 Toán 6 Kết nối tri thức tập 1
Các bạn hãy tham khảo ngay phương pháp giải chi tiết và chính xác nhất của các câu hỏi hoạt động, luyện tập và vận dụng thuộc mục 4 Trừ hai số nguyên ở trang 70, 71 Toán 6 KNTT ngay dưới đây nhé.
Hoạt động 7 trang 70
Giải bài toán trên bằng hai cách:
Cách 1. Tính hiệu giữa số tiền lãi và số tiền lỗ.
Cách 2. Hiểu lỗ 2 triệu là “lãi” -2 triệu để quy về tính tổng của hai số nguyên.
Giải bài toán theo 2 cách đề bài đưa ra.
Cách 1: Hiệu giữa số tiền lãi và số tiền lỗ là: $5 – 2 = 3$
Vậy cửa hàng đó lãi 3 triệu đồng
Cách 2: Lỗ 2 triệu nghĩa là lãi (-2) triệu
Vậy cửa hàng đó lãi: $5 + (-2) = 3$ (triệu đồng)
Hoạt động 8 trang 70
$3-1=3+(-1)$
$3-2=3+(-2)$
$3-3=3+(-3)$
$3-4=?$
$3-5=?$
Quan sát ba dòng đầu và dự đoán kết quả ở hai dòng cuối.
Dự đoán:
$3 – 4 = 3 + (-4)$
$3 – 5 = 3 + (-5)$
Luyện tập 5 trang 71
a) $5-(-3)$
b) $(-7)-8$
Muốn trừ số nguyên $a$ cho số nguyên $b$, ta cộng $a$ với số đối của $b$:
$a – b = a + (-b)$.
a) $5 – (-3) = 5 + 3 = 8$
b) $(-7) – 8 = (-7) + (-8) = -(7+8)= -15$
Vận dụng 3 trang 71
Nhiệt độ chênh lệch $=$ Nhiệt độ ở sân bay khi hạ cánh $–$ Nhiệt độ bên ngoài của máy bay ở độ cao $10 000 \mathrm{~m}$
Nhiệt độ bên ngoài của máy bay ở độ cao $10 000 \mathrm{~m}$ và khi hạ cánh chênh lệch nhau:
$27 – (-48) = 27 + 48 = 75$ (độ $C$)
Giải SGK bài tập trang 71 Toán 6 Kết nối tri thức tập 1
Cuối cùng là hướng dẫn và lời giải chi tiết nhất cho các bài tập nằm ở trang 71 Toán 6 KNTT. Cũng giống như các mục trên, những phương pháp giải sau đây tin chắc sẽ giúp bạn hiểu thêm về cách giải và vận dụng vào những bài tập tương tự sau này.
Bài 3.9 trang 71
a) $(-7)+(-2)$;
b) $(-8)+(-5)$;
c) $(-11)+(-7)$;
d) $(-6)+(-15)$.
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “$-$” trước kết quả.
a) $(-7) + (-2) = -(7 + 2) = -9$
b) $(-8) + (-5) = -(8 + 5) = -13$
c) $(-11) + (-7) = -( 11 + 7) = -18$
d) $(-6) + (-15) = -(6 + 15) = -21$
Bài 3.10 trang 71
a) $6+(-2)$;
b) $9+(-3)$;
c) $(-10)+4$;
d) $(-1)+8$.
Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
a) $6 + (-2) = 6 – 2 = 4$
b) $9 + (-3) = 9 – 3 = 6$
c) $(-10) + 4 = -(10 – 4) = -6$
d) $(-1) + 8 = 8 – 1 = 7$
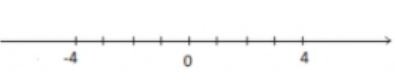
Bài 3.11 trang 71
Trên trục số hai điểm có cùng khoảng cách đến gốc $O$ được gọi là hai số đối nhau.
Bài 3.12 trang 71
a) $9-(-2)$;
b) $(-7)-4$;
c) $27-30$;
d) $(-63)-(-15)$.
Muốn trừ số nguyên $a$ cho số nguyên $b$, ta cộng $a$ với số đối của $b$: $a – b = a + (-b)$.
a) $9 – (-2) = 9 + 2 = 11$
b) $(-7) – 4 = -7+ (-4) = -(7 + 4) = -11$
c) $27 – 30 = 27+ (-30) = -(30 – 27) = -3$
d) $(-63) – (-15) = (-63) + 15 = -(63 -15)= – 48$
Bài 3.13 trang 71
Giả sử có một con ếch nhảy dọc theo một trục số. Đầu tiên ếch nhảy từ gốc $O$ đến điểm $A$ biểu diễn số 4 . Tiếp theo, ếch nhảy theo chiều ngược lại đến điểm $B$ cách điểm $A$ một khoảng bằng 6 đơn vị. Hỏi điểm $B$ biểu diễn số nào trên trục số?
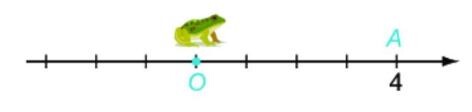
Con ếch nhảy theo chiều ngược lại \Longrightarrow Thực hiện phép trừ.

Bài 3.14 trang 71
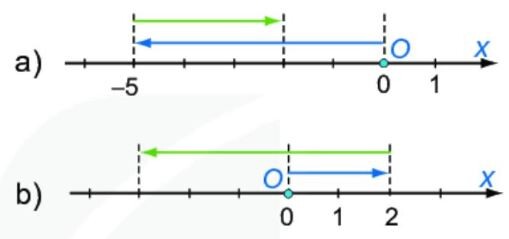
Khi di chuyển chiều sang phải trục số ta thực hiện phép cộng, di chuyển sang trái ta thực hiện phép trừ.
a) Hình vẽ mô tả phép tính: $0 – 5 + 3 = -2$
b) Hình vẽ mô tả phép tính: $0 + 2 – 5 = -3$
Bài 3.15 trang 71
a) $(-3)+(-2)$;
b) $(-8)-7$;
c) $(-35)+(-15)$;
d) $12-(-8)$.
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “$-$” trước kết quả.
Muốn trừ số nguyên $a$ cho số nguyên $b$, ta cộng $a$ với số đối của $b$: $a – b = a + (-b)$.
a) $(-3) + (-2) = -(3 + 2) = -5$
b) $(-8) – 7 = (-8) + (-7) = -(8 + 7) = -15$
c) $(-35) + (-15) = -(35 + 15) = -50$
d) $12 – (-8) = 12 + 8 = 20$
Bài 3.16 trang 71
a) $152+(-73)-(-18)-127$;
b) $7+8+(-9)+(-10)$.
Áp dụng tính chất giao hoán và phân phối của phép cộng.
a) $152 + (-73) – (-18) – 127 = 152 – 73 +18 -127 = (152 + 18) – (127 + 73) = 170 – 200 = -(200 – 170) = -30$
b) $7 + 8 + (-9) + (-10) = (7 + 8) + [(-9) + (-10)] = 15 + (-19) = -(19 – 15)= -4$
Bài 3.17 trang 71
a) $x=-26$;
b) $x=76$;
c) $x=(-28)-(-143)$.
– Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “$-$” trước kết quả.
Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng ( số lớn trừ số bé) rồi đặt trước kết quả tìm được dấu của số có phần số tự nhiên lớn hơn.
Muốn trừ số nguyên $a$ cho số nguyên $b$, ta cộng $a$ với số đối của $b$: $a – b = a + (-b)$.
a) $(-156) – x = (-156) – (-26) = (-156) + 26 = -(156 – 26) = -130$
b) $(-156) – x = (-156) – 76 = (-156) + (-76) = – (156 + 76)= -232$
c) Cách 1:
$(-156) – x = (-156) – [(-28) – (-143)] = (-156) – [(-28) + 143] = (-156) + 28 – 143 = (-156) + 28 + (-143)= (-128) + (-143) = -(128+143) = -271$
Cách 2:
$(-156) – x = (-156) – [(-28) – (-143)] = (-156) – [(-28) + 143] = (-156) – 115 = (-156 +115)= -271$
Bài 3.18 trang 71
a) $\left(-\overline{6^{\star}}\right)+(-34)=-100$;
b) $(-789)+\overline{2^{\star \star}}=-515$.
Muốn tìm số hạng ta lấy hiệu trừ đi số hạng còn lại.
a) $\left(-\overline{6^{\star}}\right)+(-34)=-100$
$\left(-\overline{6^{\star}}\right)=-100 – (-34)$
$\left(-\overline{6^{\star}}\right)=-100 + 34$
$\left(-\overline{6^{\star}}\right)=-66$
Vậy dấu \ast là chữ số $6$.
b) $(-789)+\overline{2^{\star \star}}=-515$
$\overline{2^{\star \star}}=-515 – (-789)$
$\overline{2^{\star \star}}=-515 + 789)$
$\overline{2^{\star \star}}= 274$
Vậy hai dấu \ast lần lượt là $7$ và $4$.
Bài Giải SGK bài 14 Phép cộng và phép trừ số nguyên Toán 6 KNTT tập 1 đã hoàn thành. Hy vọng bài viết có thể giúp bạn nắm và hiểu rõ hơn về cách làm bài. Cảm ơn các bạn đã theo dõi bài viết của HọcThatGioi. Hẹn gặp lại các bạn vào các bài viết tiếp theo nhé!





