Giải SGK Bài 15 trang 75, 76, 77, 78, 79 SGK Toán 7 Kết nối tri thức Tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi, vận dụng, luyện tập và bài tập trong bài Các trường hợp bằng nhau của tam giác vuông. Các bài tập sau đây thuộc Bài 15 chương 4 trang 75, 76, 77, 78, 79 Toán 7 Kết nối tri thức Tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 75, 76, 77 Toán 7 Kết nối tri thức tập 1
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi, luyện tập và vận dụng ở các trang 75, 76, 77 trong bài Các trường hợp bằng nhau của tam giác vuông ở ngay bên dưới nhé!
Giải hoạt động 1 trang 75 SGK Toán 7 Kết nối tri thức
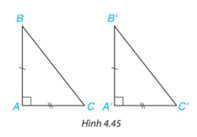
Chứng minh hai cạnh và góc xen giữa của hai tam giác trên bằng nhau.
Xét 2 tam giác ABC và A’B’C có:
$AB=A’B’$ (gt)
\widehat{A} = \widehat{A’}
$AC = AC’$ (gt)
$ \Longrightarrow$ $\Delta$ $ABC$ = $\Delta$ $A’B’C’$ (c.g.c)
Giải hoạt động 2 trang 76 SGK Toán 7 Kết nối tri thức
Dựa vào trường hợp bằng nhau góc cạnh – góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông $ABC$ và $ABC$ bằng nhau.
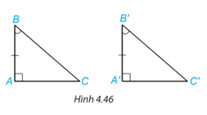
Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh – góc.
Xét 2 tam giác ABC và A’B’C’ có:
\widehat{B} = \widehat{B’} (gt)
$AB=A’B’$ (gt)
\widehat{A} = \widehat{A’} (gt)
$\Longrightarrow$ $\Delta$ $ABC$ = $\Delta$ $A’B’C’$
Giải Luyện tập 1 trang 76 SGK Toán 7 Kết nối tri thức
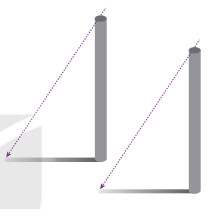
Áp dụng trường hợp bằng nhau của tam giác vuông.
Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau ( g-c-g).
Giải hoạt động 3 trang 76 SGK Toán 7 Kết nối tri thức
a) Dựa vào trường hợp bằng nhau góc – cạnh – góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
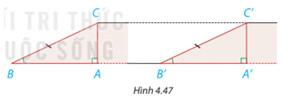
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – góc nhọn
b) Chứng minh $AC=A’C’$
a)Xét hai tam giác vuông ABC và A’B’C’ có:
$BC=B’C’$ (gt)
\widehat{ABC} = \widehat{A’B’C’} (cạnh huyền – góc nhọn)
b) Do $\Delta$ $ABC$ = $\Delta$ $A’B’C’$ nên nên $AC=A’C’$ ( 2 cạnh tương ứng)
Vậy độ cao hai con dốc bằng nhau.
Giải câu hỏi SGK trang 76 Toán 7 Kết nối tri thức
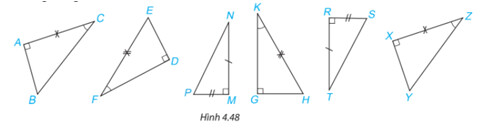
Chứng minh ba cặp tam giác vuông bằng nhau theo các trường hợp bằng nhau đã học.
+)Xét hai tam giác vuông ABC và XYZ có:
\widehat{A} = \widehat{X} (= 90^{\circ})
$AC=XZ$ (gt)
\widehat{C} = \widehat{Z} (gt)
$ \Longrightarrow$ $\Delta$ $ABC$ = $\Delta$ $XYZ$ (g.c.g)
+)Xét hai tam giác vuông $DEF$ và $GHK$ có:
$EF = HK$ (gt)
$\Longrightarrow$ $\Delta$ $DEF$= $\Delta$ $GHK$ (cạnh huyền – góc nhọn)
+Xét hai tam giác vuông NMP và RTS có:
$MN$ = $TR$ (gt)
\widehat{R} = \widehat{M} (= 90^{\circ})
$AC$=$XZ$ (gt)
$PM$ = $SR$ (gt)
$\Longrightarrow $ $\Delta$ $MNP$= $\Delta$ $RTS$ (c.g.c)
Giải Luyện tập 2 trang 77 SGK Toán 7 Kết nối tri thức
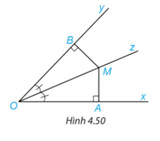
Chứng minh hai tam giác OBM và OAM bằng nhau.
Xét hai tam giác vuông OBM và OAM có:
$OM$ chung
$ \widehat {BOM}$ = $\widehat {OAM}$
$ \Longrightarrow $ $\Delta$ $ABC$ = $\Delta$ $XYZ$ (cạnh huyền – góc nhọn)
Suy ra $MB$ = $MA$ (2 cạnh tương ứng)
Giải hoạt động 4 trang 78 SGK Toán 7 Kết nối tri thức
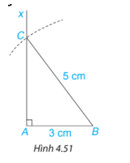
• Dùng thước thẳng có vạch chia vẽ đoạn thẳng $AB$ = 3 cm.
• Vẽ tia $Ax$ vuông góc với $AB$ và cung tròn tâm $B$ bán kính 5 cm như Hình 4.51.
Cung tròn cắt tia $Ax$ tại điểm $C$.
•Vẽ đoạn thẳng $BC$ ta được tam giác ABC.
Vẽ tam giác theo các bước hướng dẫn.
Giải hoạt động 5 trang 78 SGK Toán 7 Kết nối tri thức
a) Dùng thước thẳng có vạch chia hoặc compa kiểm tra xem $AC$ có bằng $A’C’$ không?
b) Hai tam giác ABC và A’B’C’ có bằng nhau không?
Dùng thước thẳng hoặc compa kiểm tra.
a) Dùng thước thẳng có vạch chia hoặc compa kiểm tra được $AC$ = $A’C’$
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì 3 cặp cạnh đều bằng nhau
Giải câu hỏi SGK trang 78 Toán 7 Kết nối tri thức tập 1
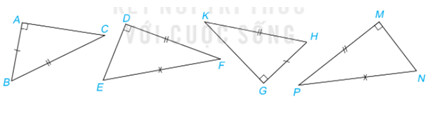
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Xét hai tam giác ABC vuông tại $A$ và GHK vuông tại $G$ có:
$AB = GH$ (gt)
$BC = HK$ (gt)
Do đó (cạnh huyền – cạnh góc vuông).
Xét hai tam giác DEF vuông tại $D$ và MNP vuông tại $M$ có:
$DF = MP$ (gt)
$EF = NP$ (gt)
Do đó (cạnh huyền – cạnh góc vuông).
Vậy $\Delta$ $ABC$ = $\Delta$ $GHK$, $\Delta$ $DEF$ = $\Delta$ $MNP$.
Giải Luyện tập 3 trang 79 SGK Toán 7 Kết nối tri thức
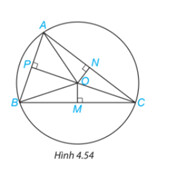
Quan sát hình vẽ và chỉ ra 3 cặp tam giác vuông bằng nhau.
Vì $A$, $B$, $C$ nằm trên đường tròn tâm $O$ nên $OA$ = $OB$ = $OC$.
Xét hai tam giác ONA vuông tại $N$ và ONC vuông tại $N$ có:
$OA = OC$ (cmt)
$ON$ chung
$\Delta$ $ONA$ = $\Delta$ $ONC$ (cạnh huyền – cạnh góc vuông).
Xét hai tam giác $OMB$ vuông tại $M$ và $OMC$ vuông tại $M$ có:
$OB = OC$ (cmt)
$OM$ chung
$\Delta$ $OMB$ = $\Delta$ $OMC$ (cạnh huyền – cạnh góc vuông).
Xét hai tam giác $OPA$ vuông tại $P$ và $OPB$ vuông tại $P$ có:
$OA = OB$ (cmt)
$OP$ chung
Do đó, $\Delta$ $OPA$ = $\Delta$ $OPB$ (cạnh huyền – cạnh góc vuông).
Giải thử thách nhỏ SGK Trang 79 Kết nối tri thức
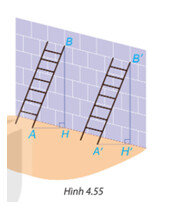
Chứng minh hai tam giác BAH và B’A’H’ bằng nhau, từ đó suy ra 2 góc bằng nhau.
Xét hai tam giác BAH và B’A’H’ có:
$AB=A’B’$
$BH=B’H’$
Suy ra ( cạnh huyền – cạnh góc vuông)
\Longrightarrow (hai góc tương ứng).
Giải bài tập SGK trang 79 Toán 7 Kết nối tri thức tập 1
Những bài tập SGK ở cuối bài Tập hợp các số thực trang 36 sách Toán 7 Kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Giải bài 4.20 SGK trang 79 Toán 7 Kết nối tri thức
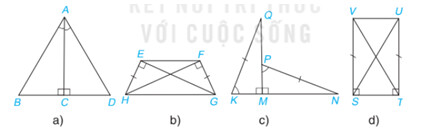
Áp dụng các trường hợp bằng nhau của 2 tam giác vuông để chứng minh các cặp tam giác trên bằng nhau.
a) Xét 2 tam giác vuông ABC và ADC có:
\ \widehat{ACB} = \widehat{ACD} = 90^{\circ}
$AC$ chung
\ \widehat{BAC} = \widehat{DAC} (gt)
$\Longrightarrow$ $\Delta$ $ABC$ = $\Delta$ $ADC$ (g.c.g)
b) Xét 2 tam giá vuông $HEG$ và $GFH$ có:
$HE = GF$ (gt)
$HG$ chung
$ \Longrightarrow$ $\Delta$ $HEG$ = $\Delta$ $GFH$ (cạnh huyền góc vuông)
c) Xét 2 tam giác vuông $QMK$ và $NMP$ có:
$QK = NP$ (gt)
\ \widehat{K} = \widehat{P} (gt)
$\Longrightarrow$ $ \Delta$ $QMK$ = $\Delta$ $NMP$ (cạnh huyền góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
$VS=UT$ (gt)
$ST$ chung
$\Longrightarrow$ $\Delta$ $VST$ = $\Delta$ $UTS$ ( 2 cạnh góc vuông)
Giải bài 4.21 SGK trang 79 Toán 7 Kết nối tri thức
Chứng minh rằng: $ \Delta$ $ABE$ = $\Delta$ $DCE$
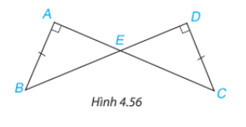
Chứng minh 2 tam giác vuông AEB và DEC bằng nhau theo trường hợp góc – cạnh – góc.
Vì tổng 3 góc trong 1 tam giác luôn bằng $180$ độ.
Xét hai tam giác AEB và DEC có:
\widehat{ABE} = \widehat{DEC} (đối đỉnh) và \widehat{BAC} = \widehat{BDC} = 90^{\circ}
Suy ra: \widehat{ABE} = \widehat{DCE}
Xét 2 tam giác $AEB$ và $DEC$ có:
\widehat{BAC} = \widehat{BDC} = 90^{\circ}
$AB = DC$(gt)
\widehat{ABE} = \widehat{DCE} (cmt)
$\Delta$ $ABE$ = $\Delta$ $DEC$
Giải bài 4.22 SGK trang 79 Toán 7 Kết nối tri thức
Chứng minh rằng $\Delta$ $ABM$ = $\Delta$ $DCM$
Chứng minh 2 tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.
Vì $ABCD$ là hình chữ nhật nên $AB = DC$
$ \Delta$ $ABM$ = $\Delta$ $DCM$ = 90^{\circ} (tính chất hình chữ nhật)
Xét 2 tam giác $ABM$ và $DCM$ có:
$AB=DC$ (cmt)
$\Delta$ $ABM$ = $\Delta$ $DCM$ (cmt)
$BM = CM$ (gt)
$\Delta$ $ABM$ = $\Delta$ $DCM$ (g.c.g)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hy vọng, qua bài viết này bạn có thể nắm rõ tất cả các kiến thức có trong Bài 15 Trường hợp bằng nhau của tam giác vuông trang 75, 76, 77, 78, 79 SGK Toán 7 Kết nối tri thức Tập 1. Chúc các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





