Giải SGK bài 16 Phép nhân số nguyên Toán 6 Kết nối tri thức tập 1
Bài viết dưới đây tổng hợp các phương pháp và lời giải chi tiết về các hoạt động, luyện tập, vận dụng, thử thách và bài tập của bài 16 Phép nhân số nguyên nằm ở các trang 75, 76, 77 SGK Toán 6 Kết nối tri thức tập 1. Các phương pháp và lời giải của HocThatGioi hy vọng sẽ giúp bạn nắm rõ được bài học, tiếp thu thêm kiến thức để làm tốt các bài tương tự sau này. Cùng theo dõi ngay nhé!
Giải SGK câu hỏi mục 1 trang 75 Toán 6 KNTT tập 1
Dưới đây là phương pháp và lời giải chi tiết cho các câu hỏi hoạt động, luyện tập và vận dụng ở mục 1 Nhân hai số nguyên khác dấu trang 75 bài 16 Toán 6 KNTT tập 1. Các bạn có thể xem ngay đáp án bên dưới nhé!
Hoạt động 1 trang 75
$(-a) \cdot n = (-a) \cdot (-a)…(-a)$ ($n$ thừa số $a$)
$(-11) \cdot 3 = (-11) + (-11) + (-11) = -33$
$-(11 \cdot 3) = -(11 + 11 + 11) = -33$
Vậy $(-11) \cdot 3 = -(11 \cdot 3)$
Hoạt động 2 trang 75
Dựa vào HĐ1 để dự đoán.
Dự đoán:
$5 \cdot (-7) = -(5 \cdot 7) = -35$
$(-6) \cdot 8 = -(6 \cdot 8) = -48$
Luyện tập 1 trang 75
a) $(-12) \cdot 12$;
b) $137 \cdot (-15)$.
2. Tính nhẩm: $5 \cdot (-12)$.
Nếu m, n \ \epsilon \ \mathbb{N} ^ \ast thì: $m \cdot (-n) = (-n) \cdot m = -(m \cdot n)$.
1. a) $(-12) \cdot 12 = -(12 \cdot 12) = -144$
b) $137 \cdot (-15) = -(137 \cdot 15) = – 2 055$
2. $5 \cdot (-12) = -(5 \cdot 12) = -60$
Vận dụng 1 trang 75
Tổng số tiền Cao đã ghi = Số tiền ghi 1 lần $\cdot$ Số lần ghi
Cao đã ghi $3$ lần, mỗi lần $-15 000$ đồng nên tổng số tiền Cao đã ghi là: $(-15 000) \cdot 3 = -(15 000 \cdot 3) = -45 000$ (đồng)
Vậy Cao đã chi $45 000$ đồng.
Giải SGK câu hỏi mục 2 trang 76 Toán 6 KNTT tập 1
Tiếp theo là phương pháp và lời giải chi tiết cho các câu hỏi hoạt động, luyện tập và thử thách nhỏ thuộc mục 2 Nhân hai số nguyên cùng dấu trang 76 bài 16 Toán 6 KNTT tập 1. Các bạn cùng tham khảo ngay đáp án bên dưới nhé!
Hoạt động 3 trang 76

Quan sát ba dòng đầu và nhận xét.
Nhận xét: khi đổi dấu một thừa số và giữ nguyên thừa số còn lại thì tích cũng đổi dấu.
Hoạt động 4 trang 76
Đổi dấu tích của phép tính thứ ba.
Theo HĐ3, nếu đổi dấu một thừa số thì tích cũng đổi dấu nên ta dự đoán tích đổi dấu $-21$ thành $21$
Vậy dự đoán $(-3) \cdot (-7) = 21$
Luyện tập 2 trang 76
a) $(-12) \cdot (-12)$;
b) $(-137) \cdot (-15)$.
Nếu m, n \ \epsilon \ \mathbb{N} ^ \ast thì: $(-m) \cdot (-n) = m \cdot n$.
a) $(-12) \cdot (-12) = 12 \cdot 12 = 144$
b) $(-137) \cdot (-15) = 137 \cdot 15 = 2055$.
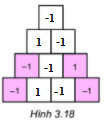
Thử thách nhỏ trang 76
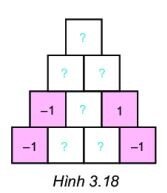
Nếu m, n \ \epsilon \ \mathbb{N} ^ \ast thì: $(-m) \cdot (-n) = m \cdot n$.
Mà mỗi ô ở hàng trên bằng tích các số trong hai ô kề với nó ở hàng dưới nên ta được :
Giải SGK câu hỏi mục 3 trang 76, 77 Toán 6 KNTT tập 1
Tiếp đến là phương pháp và lời giải chi tiết cho câu hỏi và luyện tập thuộc mục 3 Tính chất của phép nhân trang 76, 77 bài 16 Toán 6 KNTT tập 1. Các bạn hãy cùng tham khảo ngay đáp án bên dưới nhé!
Câu hỏi trang 76
Thay giá trị của $a, b, c$ vào biểu thức cần tính.
Với $a = -2, b = 14, c = -4$ ta có:
$a(b + c) = (-2) \cdot [14 + (-4)] = (-2) \cdot 10 = -(2 \cdot 10) = -20$
$ab + ac = (-2) \cdot 14 + (-2) \cdot (-4) = -28 + 8 = -(28 – 8) = -20$.
Luyện tập 3 trang 77
b) Tích $P$ sẽ thay đổi thế nào nếu ta đổi dấu tất cả các thừa số?
2. Tính $4 \cdot(-39)-4 \cdot(-14)$.
Áp dụng các tính chất:
Giao hoán: $a \cdot b = b \cdot a$
Kết hợp: $a \cdot (b \cdot c) = (a \cdot b) \cdot c$
Phân phối của phép nhân đối với phép cộng: $a \cdot (b + c) = ab + ac$
1.a) $P = 3 \cdot (-4).5 \cdot (-6) = [(-4) \cdot 5] \cdot [3 \cdot (-6)] = (-20) \cdot (-18) = 360$
b) Tích $P$ sẽ không thay đổi nếu ta đổi dấu tất cả các thừa số
2.
Ta có: $4 \cdot (-39) – 4 \cdot (-14) = 4 \cdot [-39 – (-14)] = 4 \cdot (-39 + 14) =4 \cdot [-(39 – 14)] = 4 \cdot (-25) = -100$
Chú ý: Tích không thay đổi nếu ta đổi dấu của $n$ thừa số (với $n$ chẵn)
Tích thay đổi dấu nếu ta đổi dấu của $n$ thừa số (với $n$ lẻ)
Giải SGK bài tập trang 77 Toán 6 KNTT tập 1
Dưới đây là phương pháp và lời giải chi tiết cho các bài tập nằm ở trang 77 bài 16 Toán 6 KNTT tập 1. Các lời giải bài tập sau đây sẽ giúp bạn nắm chắc kiến thức đã học và vận dụng nó cho các bài tập khác sau này. Hãy cùng xem ngay nhé!
Bài 3.32 trang 77
b) $(-15) \cdot 12$.
Nếu m, n \ \epsilon \ \mathbb{N} ^ \ast thì: $m \cdot (-n) = (-n) \cdot m = -(m \cdot n)$.
a) $24 \cdot (-25) = – ( 24 \cdot 25) = -600$
b) $(-15) \cdot 12 = -(15 \cdot 12) = -180$.
Bài 3.33 trang 77
a) $(-298) \cdot(-4)$;
b) $(-10) \cdot(-135)$.
Nếu m, n \ \epsilon \ \mathbb{N} ^ \ast thì: $(-m) \cdot (-n) = m \cdot n$.
a) $(-298) \cdot (-4) = 298 \cdot 4 = 1 192$
b) $(-10) \cdot (-135) = 10 \cdot 135 = 1 350$
Bài 3.34 trang 77
a) Ba thừa số mang dấu âm, các thừa số khác đều dương?
b) Bốn thừa số mang dấu âm, các thừa số khác đều dương?
Trong phép tính có lẻ các thừa số âm \Longrightarrow Tích mang dấu âm.
Trong phép tính có chẵn các thừa số âm \Longrightarrow Tích mang dấu dương.
a) Ba thừa số mang dấu âm, các thừa số khác dấu dương thì tích mang dấu âm.
b) Bốn thừa số mang dấu âm, các thừa số khác đều dương thì tích mang dấu dương.
Bài 3.35 trang 77
a) $4 \cdot(1930+2019)+4 \cdot(-2019)$;
b) $(-3) \cdot(-17)+3 \cdot(120-17)$.
Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
$a \cdot (b + c) = ab + ac$
a) $4 \cdot (1 930 + 2 019) + 4 \cdot (-2 019)$
$= 4 \cdot (1 930 + 2 019 – 2 019)$
$= 4 \cdot 1 930 = 7 720$
b) $(-3) \cdot (-17) + 3 \cdot (120 – 17)$
$= 3 \cdot 17 + 3 \cdot (120 – 17)$
$= 3 \cdot (17 + 120 – 17)$
$= 3 \cdot 120 = 360$
Bài 3.36 trang 77
Sử dụng: $n \cdot(-m) = -(n \cdot m)$
$(-n) \cdot(-m) = n \cdot m$
Ta có: $n \cdot m = 36$
$n \cdot (-m) = -(n \cdot m) = -36$
$(-n) \cdot (-m) = n \cdot m = 36$
Bài 3.37 trang 77
a) $(-8) \cdot 72+8 \cdot(-19)-(-8)$;
b) $(-27) \cdot 1011-27 \cdot(-12)+27 \cdot(-1)$.
Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
$a \cdot (b + c) = ab + ac$.
a) $(-8) \cdot 72 + 8 \cdot (-19) – (-8)$
$= (-8) \cdot 72 + (-8) \cdot 19 – (-8) \cdot 1$
$= (-8) \cdot (72 + 19 – 1)$
$= (-8) \cdot 90$
$= -720$
b) $(-27) \cdot 1011 – 27 \cdot (-12) + 27 \cdot (-1)$
$= 27 \cdot (-1011) – 27 \cdot (-12) + 27 \cdot (-1)$
$= 27 \cdot (-1011 + 12 – 1)$
$= 27 \cdot (-1 000)$
$= -27 000$
Bài 3.38 trang 77
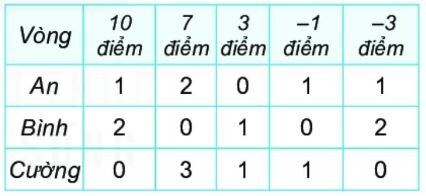

Dựa vào bảng tính số điểm của mỗi bạn rồi so sánh.
Số điểm của An là: $10 \cdot 1 + 2 \cdot 7 + 1 \cdot (-1) + 1 \cdot (-3) =10 + 14 + (-1) + (-3) = 20$
Số điểm của Bình là: $2 \cdot 10 + 1 \cdot 3 + 2 \cdot (-3) = 20 + 3 + (-6) = 17$
Số điểm của Cường là: $3 \cdot 7 + 1 \cdot 3 + 1 \cdot (-1) = 21 + 3 + (-1) = 23$
Vì $17 < 20 < 23$ nên bạn Cường đạt điểm cao nhất.
Bài viết trên của HocThatGioi đã tổng hợp phương pháp và lời giải chi tiết cho các câu hỏi hoạt động, luyện tập, vận dụng, thử thách và bài tập thuộc bài 16 Phép nhân số nguyên trang 75, 76, 77 SGK Toán 6 Kết nối tri thức tập 1. Hy vọng bài viết giúp các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tập tốt và hẹn gặp lại các bạn ở các bài viết sau.





