Giải SGK bài 3 trang 59, 60, 61, 62, 63 Toán 10 Chân trời sáng tạo tập 2
Đường tròn trong mặt phẳng tọa độ là bài học thuộc bài 3 chương 9 Toán 10 Chân trời sáng tạo tập 2. Dưới đây là những lời giải cực chi tiết của HocThatGioi cho những hoạt động khám phá, thực hành, vận dụng cũng như bài tập sách giáo khoa ở các trang 59, 60, 61, 62, 63 mà các bạn sẽ được học trong bài này. Cùng theo dõi ngay nhé!
Trả lời câu hỏi SGK bài Đường tròn trong mặt phẳng tọa độ
Các hoạt động khám phá, thực hành, vận dụng luyện tập ở các trang 59, 60, 61, 62 này sẽ giúp các bạn đi vào bài học tìm hiểu các kiến thức về Đường tròn trong mặt phẳng tọa độ một cách trơn tru và dễ hiểu hơn rất nhiều đấy! Cùng xem lời giải của HocThatGioi nhé!
Hoạt động khởi động trang 59
Tập hợp các điểm xa nhất mà vòi này có thể phun tới là đường tròn có tâm là tâm một vòi phun.
Sau bài học này ta có thể viết được phương trình biểu diến tập hợp các điểm xa nhất mà vòi này có thể phun tới là phương trình đường tròn có tâm là điểm có tọa độ (30; 40) và bán kính là 50 có dạng: (x-30^2)+(y-40)^2=50^2
Hoạt động khám phá 1 trang 59
Khoảng cách hai điểm $M, I$ (hay độ dài đoạn thẳng MI) chính là độ dài vecto $\overrightarrow{M I}$
\overrightarrow{M I}=(a-x ; b-y) \Rightarrow|\overrightarrow{M I}|=\sqrt{(a-x)^2+(; b-y)^2}
Vậy khoảng cách giữa hai điểm $I(a ; b)$ và $M(x ; y)$ là \sqrt{(a-x)^2+(; b-y)^2}
Thực hành 1 trang 60
a) (C) có tâm $O(0 ; 0)$, bán kính $R=4$;
b) (C) có tâm $I(2 ;-2)$, bán kính $R=8$;
c) $(C)$ đi qua ba điểm $A(1 ; 4), B(0 ; 1), C(4 ; 3)$.
Phương trình đường tròn tâm $I(a ; b)$ và bán kính $R$ là $(x-a)^2+(y-b)^2=R^2$
c) Lập phương trình đường trung trực của 2 cạnh => có giao điểm là tâm I cần tìm.
Từ đó tính bán kính R và lập pt đường tròn.
a) Đường tròn $(C)$ tâm $O(0 ; 0)$, bán kính $R=4$ có phương trình là: $x^2+y^2=16$
b) Đường tròn (C) tâm $I(2 ;-2)$, bán kính $R=8$ có phương trình: $(x-2)^2+(y+2)^2=64$
c) Gọi $M, N$ lần lượt là trung điểm của $A B, A C$ ta có: $M\left(\frac{1}{2} ; \frac{5}{2}\right), N\left(\frac{5}{2} ; \frac{7}{2}\right)$
Đường trung trực $\Delta$ của đoạn thẳng $A B$ là đường thẳng đi qua $M$ và nhận vt $\overrightarrow{B A}=(1 ; 3)$ làm vt pháp tuyến, nên có phương trình $x+3 y-8=0$
Đường trung trực $d$ của đoạn thẳng $A C$ là đường thẳng đi qua $N$ và nhận vt $\overrightarrow{A C}=(3 ;-1)$ làm vt pháp tuyến, nên có phương trình $3 x-y-4=0$
$\Delta$ cắt $d$ tại điểm $I(2 ; 2)$ cách đều ba điểm $A, B, C$ suy ra đường tròn (C) cần tìm có tâm $I(2 ; 2)$ và có bán kính $R=I A=\sqrt{5}$.
Vậy (C) có phương trình: $(x-2)^2+(y-2)^2=5$
Thực hành 2 trang 61
a) $x^{2}+y^{2}-2 x-4 y-20=0$;
b) $(x+5)^{2}+(y+1)^{2}=121$
c) $x^{2}+y^{2}-4 x-8 y+5=0$
d) $2 x^{2}+2 y^{2}+6 x+8 y-2=0$.
– Phương trình có dạng $(x-a)^2+(y-b)^2=R^2$ là đường tròn với tâm $I(a ; b)$ và bán kính $\mathrm{R}$
– Phương trình $x^2+y^2-2 a x-2 b y+c=0$ là phương trình đường tròn khi và chỉ khi $a^2+b^2-c>0$, khi đó nó có tâm I(a;b) và bán kính $R=\sqrt{a^2+b^2-c}$
a) Phương trình đã cho có dạng $x^2+y^2-2 a x-2 b y+c=0$ với $a=1, b=2, c=-20$
Ta có $a^2+b^2-c=1+4+20=25>0$. Vậy đây là phương trình đường tròn có tâm là $I(1 ; 2)$ và có bán kính $R=\sqrt{25}=5$
b) Phương trình $(x+5)^2+(y+1)^2=121$ là phương trình dường tròn với tâm $I(-5 ;-1)$ và bán kinh $R=\sqrt{121}=11$
c) Phương trình đã cho có dạng $x^2+y^2-2 a x-2 b y+c=0$ với $a=-3, b=-2, c=-2$
Ta có $a^2+b^2-c=9+4+2=15>0$. Vậy đây là phương trình đường tròn có tâm là $I(-3 ;-2)$ và có bán kính $R=\sqrt{15}$
d) Phương trình không có dạng $x^2+y^2-2 a x-2 b y+c=0$ nên phương trình đã cho không là phương trình đường tròn
Vận dụng 1 trang 61
Tập hợp các điểm xa nhất tạo thành đường tròn với tâm I $(\mathrm{a}$; b) và bán kính R
Phương trình là: $(x-a)^2+(y-b)^2=R^2$
Theo giả thiết ta có: tâm $I(30 ; 40)$ và bán kính $R=50$
Vậy phương trình tập hợp các điểm xa nhất mà vòi nước có thể phun tới là: (x-30)^2+(y-40)^2=50^2
Vận dụng 2 trang 61
a) Tìm toạ độ tâm và bán kính của đường tròn $(C)$.
b) Cho biết tọa độ trên sân khấu của ba diễn viên $A, B, C$ như sau: $A(11 ; 4), B(8 ; 5)$, $C(15 ; 5)$. Diễn viên nào đang được đèn chiếu sáng?
a) Với phương trình thì tâm là $(x-a)^2+(y-b)^2=R^2$ thì tâm là $I(a ; b)$ và bán kính $R$
b) Bước 1: Tính khoảng cách của các diễn viên đến tâm vùng sáng
Bước 2: So sánh khoảng cách vừa tìm được với bán kính
+) Nếu nhỏ hơn hoặc bằng bán kính thì được chiếu sáng
+) Nếu lớn hơn bán kính thì không được chiếu sáng
a) (C) có phương trình $(x-13)^2+(y-4)^2=16$ nên có tâm là $I(13 ; 4)$ và bán kính $R=\sqrt{16}=4$
b) Ta có:
I A=\sqrt{(11-13)^2+(4-4)^2}=2, \\ IB=\sqrt{(8-13)^2+(5-4)^2}=\sqrt{26} \\ I C=\sqrt{(15-13)^2+(5-4)^2}=\sqrt{5}
$2\lt4 \Rightarrow IA\lt R$, suy ra diễn viên $A$ được chiếu sáng
$\sqrt{26}\gt 4 \Rightarrow I B\gt R$, suy ra diễn viên $B$ không được chiếu sáng
$\sqrt{5}\lt 4 \Rightarrow I C\lt R$, suy ra diễn viên $C$ được chiếu sáng
Vậy diễn viên A và C được chiếu sáng
Hoạt động khám phá 2 trang 61
a) Viết toạ độ của hai vectơ $\overrightarrow{M_{0} M}$ và $\overrightarrow{M_{0} I}$.
b) Viết biểu thức toạ độ của tích vô hướng của hai vectoo $\overrightarrow{M_{0} M}$ và $\overrightarrow{M_{0} I}$.
c) Phương trình $\overrightarrow{M_{0} M} \cdot \overrightarrow{M_{0} I}=0$ là phương trình của đường thẳng nào?
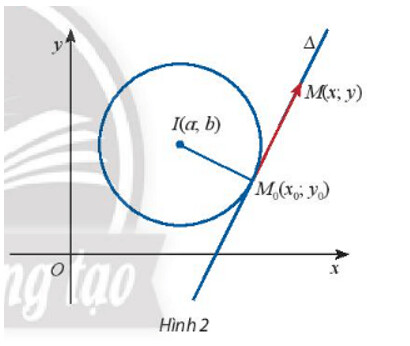
a) Với $A(a ; b), B(x ; y)$ thì tọa độ của vt $\overrightarrow{A B}=(x-a ; y-b)$
b) Với $\vec{a}=(a, b), \vec{b}=(x ; y)$ thì $\vec{a} \cdot \vec{b}=a x+b y$
c) Từ tích vô hướng đưa ra kết luận là $\overrightarrow{M_0 M}=\left(x-x_0 ; y-y_0\right)$, $\overrightarrow{M_0 I}=\left(a-x_0 ; b-y_0\right)$
a) Biểu thức tọa độ của hai vt $\overrightarrow{M_0 M}$ và $\overrightarrow{M_0 I}$ là \overrightarrow{M_0 M}=\left(x-x_0 ; y-y_0\right), \overrightarrow{M_0 I}=\left(a-x_0 ; b-y_0\right)
b) Ta có:
\overrightarrow{M_0 M} \cdot \overrightarrow{M_0 I}=\left(x-x_0\right)\left(a-x_0\right)+\left(b-y_0\right)\left(y-y_0\right) \\ \text { c) } \overrightarrow{M_0 M} \cdot \overrightarrow{M_0 I}=0 \Rightarrow \overrightarrow{M_0 M} \perp \overrightarrow{M_0 I}
Mà $M_0 I$ là đoạn thẳng nối tâm với điểm nằm ngoài
Vậy ta thấy pt đường thẳng $M M_0$ là tiếp tuyến của đường tròn tại điểm $M_0$
Thực hành 3 trang 62
Phương trình tiếp tuyến của đường tròn tâm $I(a ; b)$ tại điểm $M\left(x_0 ; y_0\right)$ nằm trên đường tròn là: \left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0
Ta có $4^2+6^2-2.4-4.6-20=0$, nên điểm $\mathrm{A}$ thuộc (C)
Đường tròn $(C): x^2+y^2-2 x-4 y-20=0$ có tâm $I(1 ; 2)$
Phương trình tiếp tuyến d của (C) tại $A(4 ; 6)$ là:
(4-1)(x-4)+(6-2)(y-6)=0 \\ \Leftrightarrow 3 x+4 y+16=0
Vận dụng 3 trang 62
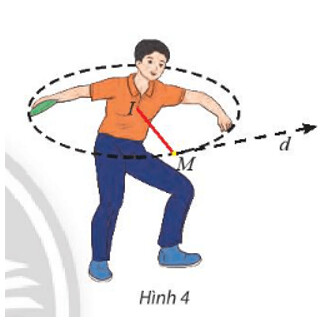
Khi người đó vung đĩa đến vị trí điểm $M\left(\frac{17}{12} ; 2\right)$ thì buông đĩa (Hình 4). Viết phương trình tiếp tuyến của đường tròn $(C)$ tại điểm $M$.
Phương trình tiếp tuyến của đường trong tâm $I(a ; b)$ tại điểm $M\left(x_0 ; y_0\right)$ nằm trên đường tròn là: \left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0
Ta có $\left(\frac{17}{12}-1\right)^2+(2-1)^2=\frac{169}{144}$, nên điểm $\mathrm{M}$ thuộc (C)
Đường tròn $(x-1)^2+(y-1)^2=\frac{169}{144}$ có tâm $I(1 ; 1)$
Phương trình tiếp tuyến d của (C) tại $M\left(\frac{17}{12} ; 2\right)$ là:
\left(\frac{17}{12}-1\right)\left(x-\frac{17}{12}\right)+(2-1)(y-2)=0 \\ \Leftrightarrow \frac{5}{2} x+y-\frac{133}{24}=0
Giải bài tập SGK bài Đường tròn trong mặt phẳng tọa độ
Những bài tập SGK ở cuối bài Đường tròn trong mặt phẳng tọa độ trang 62 sách Toán 10 Chân trời sáng tạo tập 2 sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài tập 1 trang 62
a) $x^{2}+y^{2}-6 x-8 y+21=0$,
b) $x^{2}+y^{2}-2 x+4 y+2=0$,
c) $x^{2}+y^{2}-3 x+2 y+7=0$,
d) $2 x^{2}+2 y^{2}+x+y-1=0$.
+) Phương trình $x^2+y^2-2 a x-2 b y+c=0$ là phương trình đường tròn khi và chỉ khi $a^2+b^2-c>0$, khi đó nó có tâm $\mathrm{I}(\mathrm{a} ; \mathrm{b})$ và bán kính $R=\sqrt{a^2+b^2-c}$
a) Phương trình đã cho có dạng $x^2+y^2-2 a x-2 b y+c=0$ với $a=3, b=4, c=21$
Ta có $a^2+b^2-c=9+16-21=4>0$.
Vậy đây là phương trình đường tròn có tâm là $I(3 ; 4)$ và có bán kính $R=\sqrt{4}=2$
b) Phương trình đã cho có dạng $x^2+y^2-2 a x-2 b y+c=0$ với $a=1, b=-2, c=2$
Ta có $a^2+b^2-c=1+4-2=3>0$.
Vậy đây là phương trình đường tròn có tâm là $I(1 ;-2)$ và có bán kính $R=\sqrt{3}$
c) Phương trình đã cho có dạng $x^2+y^2-2 a x-2 b y+c=0$ với $a=\frac{3}{2}, b=-1, c=7$
Ta có $a^2+b^2-c=\frac{9}{4}+1-7=-\frac{15}{4}<0$.
Vậy đây không là phương trình đường tròn.
d) Phương trình không có dạng $x^2+y^2-2 a x-2 b y+c=0$ nên phương trình đã cho không là phương trình đường tròn.
Bài tập 2 trang 62
a) $(C)$ có tâm $I(1 ; 5)$ và có bán kính $r=4$;
b) (C) có đường kính $M N$ với $M(3 ;-1)$ và $N(9 ; 3)$;
c) (C) có tâm $I(2 ; 1)$ và tiếp xúc với đường thẳng $5 x-12 y+11=0$;
d) (C) có tâm $A(1 ;-2)$ và đi qua điểm $B(4 ;-5)$.
a) Phương trình đường tròn có dạng $(x-a)^2+(y-b)^2=R^2$ với tâm $I(a ; b)$ và bán kính R
b)
– Bước 1: Từ đường kính xác định bán kính của đường tròn
– Bước 2: Xác định tâm của đường tròn (là trung điểm của đường kính)
cd)
– Bước 1: Xác định bán kính của đường tròn (là khoảng cách từ tâm đến tiếp tuyến)
– Bước 2: Viết phương trình đường tròn $(x-a)^2+(y-b)^2=R^2$ với tâm $I(a ; b)$ và bán kính R
a) Đường tròn (C) tâm $I(1 ; 5)$, bán kính $r=4$ có phương trình là: $(x-1)^2+(y-5)^2=16$
b) $M N=\sqrt{(9-3)^2+(3-(-1))^2}=2 \sqrt{13}$, suy ra bán kính là $\sqrt{13}$
Tâm của đường tròn là trung điểm của $\mathrm{MN}: I(6 ; 1)$
Đường tròn (C) tâm $I(6 ; 1)$ và bán kính là $\sqrt{13}$ có phương trình: $(x-6)^2+(y-1)^2=13$
c) Ta có bán kính của đường tròn:
r=d(I, d)=\frac{|5.2-12.1+11|}{\sqrt{5^2+12^2}}=\frac{9}{13}
Đường tròn (C) tâm $I(2 ; 1)$ và bán kính là $\frac{9}{13}$ có phương trình: $(x-2)^2+(y-1)^2=\frac{81}{169}$
d) Bán kính của đường tròn là
r=A B=\sqrt{(4-1)^2+((-5)-(-2))^2}=3 \sqrt{2}
Đường tròn (C) tâm $A(1 ;-2)$ và bán kính là $3 \sqrt{2}$ có phương trình: $(x-1)^2+(y+2)^2=18$
Bài tập 3 trang 62
a) $M(2 ; 5), N(1 ; 2), P(5 ; 4)$;
b) $A(0 ; 6), B(7 ; 7), C(8 ; 0)$.
Bước 1: Xác định tâm của đường tròn (điểm cách đều ba đỉnh của tam giác, là giao điểm của 3 đường trung trực)
Bước 2: Tính bán kính của đường tròn (là khoảng cách từ tâm đến một trong ba đỉnh)
Bước 3: Viết phương trình đường tròn $(x-a)^2+(y-b)^2=R^2$ với tâm $I(a ; b)$ và bán kính R
a) Gọi $A, B$ lân lượt là trung điếm của $M N, M P$ ta có: A\left(\frac{3}{2} ; \frac{7}{2}\right), B\left(\frac{7}{2} ; \frac{9}{2}\right)
Đường trung trực $\Delta$ của đoạn thẳng $\mathrm{MN}$ là đường thẳng đi qua $A\left(\frac{3}{2} ; \frac{7}{2}\right)$ và nhận vt $\overrightarrow{M N}=(-1 ;-3)$ làm vt pháp tuyến, nên có phương trình $-x-3 y+12=0$
Đường trung trực $\mathrm{d}$ của đoạn thẳng $\mathrm{MP}$ là đường thẳng đi qua $B\left(\frac{7}{2} ; \frac{9}{2}\right)$ và nhận vt $\overrightarrow{M P}=(3 ;-1)$ làm vt pháp tuyến, nên có phương trình $3 x-y-6=0$
$\Delta$ cắt d tại điểm $I(3 ; 3)$ cách đều ba điểm $\mathrm{M}, \mathrm{N}$, P suy ra đường tròn (C) cần tìm có tâm $I(3 ; 3)$ và có bán kính $R=I M=\sqrt{5}$.
Vậy (C) có phương trình: (x-3)^2+(y-3)^2=5
b) Gọi $M, N$ lần lượt là trung điểm của $A B, A C$ ta có: M\left(\frac{7}{2} ; \frac{13}{2}\right), N(4 ; 3)
Đường trung trực $\Delta$ của đoạn thẳng $\mathrm{AB}$ là đường thẳng đi qua $M\left(\frac{7}{2} ; \frac{13}{2}\right)$ và nhận vt $\overrightarrow{B A}=(-7 ;-1)$ làm vt pháp tuyến, nên có phương trình $-7 x-y+31=0$
Đường trung trực $\mathrm{d}$ của đoạn thẳng $\mathrm{AC}$ là đường thẳng đi qua $N(4 ; 3)$ và nhận vt $\overrightarrow{A C}=(8 ;-6)$ làm vt pháp tuyến, nên có phương trình $8 x-6 y-14=0$
$\Delta$ cắt d tại điểm $I(4 ; 3)$ cách đều ba điểm A, B, C suy ra đường tròn (C) cần tìm có tâm $I(4 ; 3)$ và có bán kính $R=I A=5$.
Vậy (C) có phương trình: (x-4)^2+(y-3)^2=25
Bài tập 4 trang 62
Bước 1: Gọi $I(a, b)$ là tâm của bán kính, giải hệ phương trình $\left\{\begin{array}{l}d(I, O x)=I A \\ d(I, O y)=I A\end{array}\right.$
Bước 2: Viết phương trình đường tròn $(x-a)^2+(y-b)^2=R^2$ với tâm $I(a ; b)$ và bán kính R
Gọi tâm của đường tròn là điểm $I(a ; b)$
Ta có:
I A=\sqrt{(a-4)^2+(b-2)^2}, d(I, O x)=b, d(I, O y) =a
Giải hệ phương trình
\left\{\begin{matrix} { d ( I , O x ) = I A } \\ { d ( I , O y ) = I A } \end{matrix} \right.
\Leftrightarrow \left\{\begin{matrix} b=\sqrt{(a-4)^2+(b-2)^2} \\ a=\sqrt{(a-4)^2+(b-2)^2} \end{matrix}\right.
Thay $a=b$ vào phương trình
a=\sqrt{(a-4)^2+(b-2)^2} \text { ta có: } \\ a=\sqrt{(a-4)^2+(a-2)^2} \\ \Rightarrow a^2=(a-4)^2+(a-2)^2 \\ \Rightarrow a^2-12 a+20=0 \\ \Rightarrow\left[\begin{array}{l} a=10 \\ a=2 \end{array}\right.
Với $a=b=2$ ta có phương trình đường tròn (C) là: (x-2)^2+(y-2)^2=4
Với $a=b=10$ ta có phương trình đường tròn (C) là: (x-10)^2+(y-10)^2=100
Bài tập 5 trang 62
a) Chứng tỏ rằng điểm $M(4 ; 6)$ thuộc đường tròn $(C)$.
b) Viết phương trình tiếp tuyến của $(C)$ tại điểm $M(4 ; 6)$.
c) Viết phương trình tiếp tuyến của $(C)$ song song với đường thẳng $4 x+3 y+2022=0$.
a) Thay tọa độ điểm $M$ vào phương trình đường tròn
+) Nếu biểu thức đó bằng 0 thì $\mathrm{M}$ thuộc đường tròn
+) Nếu biểu thức khác 0 thì $M$ không thuộc đường tròn
b) Phương trình tiếp tuyến của đường trong tâm $I(a ; b)$ tại điểm $M\left(x_0 ; y_0\right)$ nằm trên đường tròn là: $\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0$
c)
Bước 1: Xác định pt tổng quát của tiếp tuyến (biết hai đường thẳng song song với nhau thì có cùng vt pháp tuyến)
Bước 2: Xác định tiếp tuyến (biết khoảng cách từ tâm đến tiếp tuyến là bán kính)
a) Thay điểm $M(4 ; 6)$ vào phương trình đường tròn $x^2+y^2-2 x-4 y-20=0$ ta có: 4^2+6^2-2.4-4.6-20=0
Suy ra, điểm $\mathrm{M}$ thuộc đường tròn (C)
b) Đường tròn có tâm $I(1 ; 2)$
Phương trình tiếp tuyến d của (C) tại $M(4 ; 6)$ là:
(4-1)(x-4)+(6-2)(y-6)=0 \\ \Leftrightarrow 3 x+4 y+16=0
c) Tiếp tuyến của đường tròn song song với đường thẳng $4 x+3 y+2022=0$ nên phương trình có dạng $d: 4 x+3 y+c=0$
Ta có tâm và bán kính của đường tròn là: $I(1 ; 2), r=\sqrt{1^2+2^2+20}=5$
Khoảng cách từ tâm đến tiếp tuyến là bán kính nên:
$d(I, d)=\frac{|4.1+3.2+c|}{\sqrt{4^2+3^2}}=5 \\\Rightarrow\left[\begin{array}{l}c=15 \\ c=-35\end{array}\right.$
Vậy đường tròn (C) có hai tiếp tuyến song song với đường thẳng $4 x+3 y+2022=0$ là:
d_1: 4 x+3 y+15=0, d_2: 4 x+3 y-35=0
Bài tập 6 trang 62
a) Viết phương trình mô phỏng cái cổng.
b) Một chiếc xe tải rộng $2,2 \mathrm{~m}$ và cao $2,6 \mathrm{~m}$ đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không?
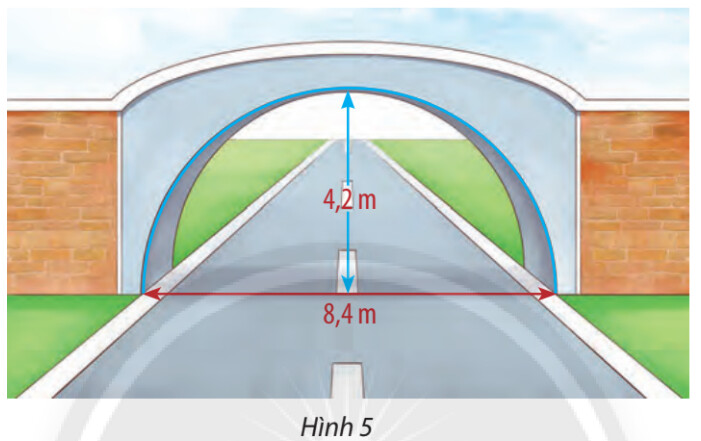
a)
Bước 1: Gắn hệ trục tọa độ vào đường
Bước 2: Viết phương trình đường tròn với điều kiện ràng buộc
b)
Bước 1: Xác định khoảng cách điểm xa nhất tới tâm đường tròn
Bước 2: So sánh kết quả vừa tìm được với bán kinh
+) Nếu nhỏ hơn hoặc bán kính thì có thể đi qua và không làm hỏng cổng
+) Ngược lại, nếu lớn hơn bánh kình thì không thể đi qua cổng
a) Ta thấy cổng có hình bán nguyệt và chiều cao của cổng bằng một nửa chiều rộng của đường nên nó có dạng nửa đường tròn
Gắn trục tọa độ tại tim đường, ta có phương trình mô phỏng cái cổng là : $x^2+y^2=4,2^2$ (với điều kiện $y>0$ vì cổng luôn nằm trên mặt đường)
b) Vì xe đi đúng làn nên ta có $x=2,2 ; y=2,6$
Khoảng cách từ điểm xa nhất của chiếc xe tài tới tim đường là: $\sqrt{2,2^2+2,6^2} \simeq 3,41$
Ta thấy rằng $3,41<4,2$, nên chiếc xe có thể đi qua cổng mà không làm hư hỏng cổng
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Đường tròn trong mặt phẳng tọa độ Toán 10 Chân trời sáng tạo tập 2 ở các trang 59, 60, 61, 62, 63. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích! Chúc các bạn học tốt!





