Phương pháp giải các dạng bài tập chuyển động thẳng đều kèm bài tập có đáp án hay nhất
Chuyển động thẳng đều là một nội dung vô cùng quan trọng trong chương trình Vật lý 10 nói riêng cũng như Vật lý THPT nói chung. Biết được điều đó, hôm nay HocThatGioi sẽ gửi đến các bạn bài viết Phương pháp giải các dạng bài tập chuyển động thẳng đều kèm bài tập có đáp án hay nhất để bạn đọc có thể nắm vững kiến thức này nhé! Khám phá ngay thôi!

Dạng 1: Xác định vận tốc, quãng đường và thời gian trong chuyển động thẳng đều. Xác định vận tốc trung bình
Phương pháp chung
Sử dụng công thức trong chuyển động thẳng đều:
S là quãng đường (m)
v là vận tốc (m/s)
t là thời gian (s)
Sử dung công thức tính tốc độ trung bình:
S là quãng đường (m)
V_{tb} là tốc độ trung bình (m/s)
t là thời gian (s)
Sử dung công thức tính vận tốc trung bình:
v là vận tốc trung bình (m/s)
x là vị trí sau (m)
x_0 là vị trí ban đầu (m)
t là vị trí sau (s)
t_0 là thời gian ban đầu (s)
Bài tập vận dụng
Bài 1:
Quãng đường đi trong 2h đầu: S_1 = v_1.t_1 = 60.2 = 120 km
Quãng đường đi trong 3h sau: S_2 = v_2.t_2 = 40.3 = 120 km
Tốc độ trung bình của xe trong suốt thời gian chuyển động: V_{tb}=\frac {S_1+S_2}{t_1+t_2} = \frac {120+120}{2+3} = 48 km/h
Bài 2:
a) Chiều dài đoạn đường AB.
b) vận tốc trung bình trên đoạn đường AB.
a) t_1 = 10 phút = 600 (s); v_1 = 36km/h = 10m/s => s_1 = v_1.t_1 = 6000 (m)
t_2 = 600 (s); v_2 = 8m/s => s_2 = v_2.t_2 = 4800 (m)
t_3 = 600 (s); v_3 = 18km/h = 5m/s => s_3 = v_3.t_3 = 3000 (m)
=> AB = s_1 + s_2 + s_3 = 13800 (m) = 13,8 (km)
b) v_{tb} = \frac {s_1 + s_2 + s_3} {t_1 + t_2 + t_3}
v_{tb}=\frac {s_1+s_2+s_3}{t_1+t_2+t_3} = 7,67 (m/s)
=> Xem thêm Lý thuyết và bài tập chuyển động thẳng đều đầy đủ chi tiết nhất – Bài 2 Vật lý 10
Dạng 2: Viết phương trình chuyển động thẳng đều, tìm thời điểm, vị trí gặp nhau của hai vật
Phương pháp chung
1. Lập phương trình chuyển động
Bước 1: Chọn hệ quy chiếu
Chọn trục tọa độ, gốc tọa độ, gốc thời gian, chiều dương của trục tọa độ.
Bước 2: Từ hệ quy chiếu vừa chọn, xác định các yếu tố x_0; v_0; t_0; x_0; v_0; t_0 của vật.
Bước 3: Viết phương trình chuyển động
- Nếu t_0 = 0 ⇒ x=x_0+vt
- Nếu t_0≠0⇒x=x_0+v(t−t_0)
Lưu ý:
- Nếu vật chuyển động cùng chiều dương thì vận tốc có giá trị dương.
- Nếu vật chuyển động ngược chiều dương thì vận tốc có giá trị âm.
2. Xác định thời điểm, vị trí hai xe gặp nhau
Bước 1: Chọn hệ quy chiếu
- Chọn trục tọa độ, gốc tọa độ, gốc thời gian, chiều dương của trục tọa độ.
- Trục tọa độ Ox trùng với quỹ đạo chuyển động
- Gốc tọa độ (thường gắn với vị trí ban đầu của vật 1 hoặc vật 2)
- Gốc thời gian (lúc vật 1 hoặc vật 2 bắt đầu chuyển động)
- Chiều dương (thường chọn là chiều chuyển động của vật được chọn làm mốc)
Bước 2: Từ hệ quy chiếu vừa chọn, xác định các yếu tố x_0; v_0; t_0; x_0; v_0; t_0 của mỗi vật.
Bước 3: Thiết lập phương trình chuyển động của mỗi vật.
Vật 1: x_1=x_{0_1}+v(t−t_{0_1}) (1)
Vật 2: x_2=x_{0_2}+v(t−t_{0_2}) (2)
Bước 4: Viết phương trình khi hai xe gặp nhau
Khi hai xe gặp nhau thì x_1=x_2 (*)
Bước 5:
Giải phương trình (*) ta tìm được thời gian t, là thời gian tính từ gốc thời gian cho đến thời điểm hai xe gặp nhau.
Thay t vào phương trình (1) hoặc (2) ta tìm được vị trí hai xe gặp nhau.
Lưu ý: Khoảng cách giữa hai vật b = |x_2 − x_1|
Bài tập vận dụng
Bài 1:
a/ Viết phương trình chuyển động.
b/ Sau khi chuyển động 30ph, người đó ở đâu ?
c/ Người đó cách A 60km lúc mấy giờ
a/ Chọn chiều dương là chiều chuyển động của xe, gốc tọa độ tại vị trí A, gốc thời gian là lúc 8h sáng.
Ta có phương trình chuyển động của xe x=x_0+vt
với x_0=0;v=40(km/h)⇒x=40t
b/ Sau khi chuyển động 30ph tức là t = 0,5h
⇒x = 40.0,5 = 20 (km)
Vậy sau 0,5h xe cách vị trí A 20 km
c/ Người đó cách A 60 km tức là x = 60km ⇒ 60 = 40t ⇒ t = \frac {60}{40}=1,5(h)
Vậy sau 1,5h xe cách vị trí A 60km
Bài 2:
Chọn gốc tọa độ tại A, gốc thời gian là lúc 7 giờ, chiều dương cùng chiều chuyển động.
Phương trình chuyển động của:
Người A: x_A=x_{0_A}+v_{A_t}= 0+50t=50t (1)
Người B: x_B=x_{0_B}+v_{B_t}=20+30t (2)
Khi hai xe gặp nhau:
x_A=x_B⇔50t=20+30t⇔t=1h
Thay t = 1 vào phương trình (1) x_A=50km
Vậy hai xe gặp nhau tại vị trí cách gốc tọa độ 50 km vào lúc 8 giờ.
Dạng 3: Đồ thị của chuyển động thẳng đều
Phương pháp chung
Nêu tính chất của chuyển động – Tính vận tốc và viết phương trình chuyển động
1. Tính chất của chuyển động
- Đồ thị xiên lên, vật chuyển động thẳng đều cùng chiều dương.
- Đồ thị xiên xuống, vật chuyển động thẳng đều ngược chiều dương.
- Đồ thị nằm ngang, vật đứng yên.
2. Tính vận tốc
Trên đồ thị ta tìm hai điểm bất kì đã biết tọa độ và thời điểm: x=\frac {x_{2}-x_{1}}{t_2-t_1}
Bài tập vận dụng
Bài 1:
a/ Lập phương trình chuyển động cho mỗi xe theo mỗi giai đoạn, chọn gốc thời gian là lúc 6h, gốc tọa độ tại A, chiều dương từ A đến B.
b/ Vẽ đồ thị tọa độ thời gian của hai xe. Từ đó hãy cho biết chúng có gặp nhau không? Khi nào và ở đâu? Kiểm tra lại bằng phép tính.
c/ Các xe đến B lúc mấy giờ?
45phút = 0,75h; 30phút = 0,5h
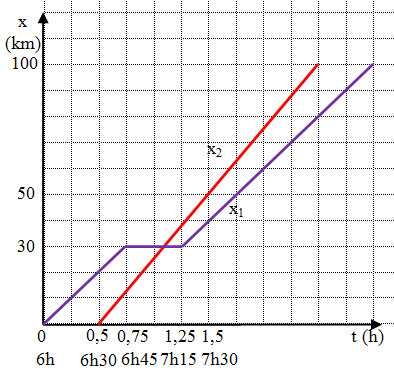
a/ Phương trình chuyển động của xe 1 từ 6h đến 6h45: x_1 = 40t
Phương trình chuyển động của xe 1 từ 6h45 đến 7h15 x_1 = 40.0,75 = 30
Phương trình chuyển động của xe 1 từ 7h15 trở đi x_1 = 30 + 40t
Phương trình chuyển động của xe 2: x_2 = 50(t – 0,5)
b/ từ đồ thị bên dưới => hai xe có gặp nhau
tọa độ gặp nhau x_1 = 30 = x_2 = 50(t – 0,5) => t = 1,1h = 1h6phút
=> hai xe gặp nhau lúc: 6h + 1h6phút = 7h6phút tại điểm cách A 30km
c/ Thời gian 1 đến B: t_1 = 100/40 + 0,5 = 3h => lúc xe 1 đến B là 9h
thời gian xe 2 đến B: t_2 = 100/50 = 2h => lúc xe 2 đến B là 8h30
Trên đây là toàn bộ bài viết Phương pháp giải các dạng bài tập chuyển động thẳng đều kèm bài tập có đáp án hay nhất. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hi vọng rằng bài viết sẽ mang lại các kiến thức bổ ích cho bạn. Hãy chia sẽ cho bạn bè để cùng nhau học thật giỏi nhé. Chúc các bạn học tốt!





