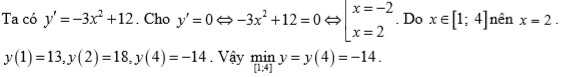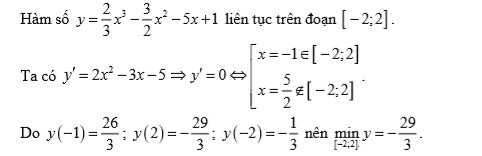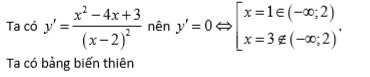Dạng bài tìm giá trị lớn nhất nhỏ nhất của hàm số trên một khoảng, một đoạn chi tiết
Cách giải chi tiết, các lưu ý quan trọng và các bài tập vận dụng về dạng bài tìm giá trị lớn nhất nhỏ nhất của hàm số trên một khoảng, một đoạn
Dạng bài tìm giá trị lớn nhất nhỏ nhất của hàm số trên một khoảng, một đoạn là dạng bài ở mức độ nhận biết, vận dụng thấp trong các đề thi. Dạng bài này tuy không khó nhưng lại rất dễ sai nếu bạn không nắm rõ được bản chất, một số câu còn đánh lừa ta nếu không đọc kĩ đề dẫn đến mất điểm vô duyên. Bài viết dưới đây, HocThatGioi sẽ hướng dẫn các bạn cách giải dạng bài này một cách chi tiết cũng như các lưu ý khi gặp dạng bài này nhé!
1. Cách giải dạng bài tìm giá trị lớn nhất nhỏ nhất của hàm số trên một khoảng, một đoạn
Dù cho đề có cho một khoảng, một đoạn hay nửa đoạn… thì khi đã nắm được bản chất, việc giải sẽ trở nên đơn giản hơn bao giờ hết.
Giả sử đề bài cho hàm số y=f(x) có tập xác định D, tìm giá trị lớn nhất (hoặc nhỏ nhất) trên đoạn [a;b]
- Bước 1: Đạo hàm y'=f'(x). Tìm các nghiệm f'(x)=0 trên đoạn [a;b]
- Bước 2: Vẽ bảng biến thiên của hàm số đó trên đoạn [a;b]
- Bước 3: Nhìn vào bảng biến thiên, ta sẽ thấy ngay được giá trị lớn nhất (hoặc nhỏ nhất) của hàm số cần tìm.
Thay vì vẽ bảng biến thiên mất thời gian, ta có thể tìm giá trị lớn nhất nhỏ nhất nhanh hơn bằng cách lần lượt tìm giá trị của f(x) ở các điểm đặc biệt f(a),f(b),f(x_0) với x_0 là nghiệm của phương trình f'(x)=0. Sau đó so sánh các giá trị trên và rút ra kết luận
Lưu ý: Cần phải nhớ thật kĩ các lưu ý dưới đây vì nó cực kì quan trọng, thứ sẽ giúp các bạn không bị mắc vào cái bẫy của người ra đề
- Nếu trên đoạn [a;b] có 1 điểm x_0 không xác định mà \lim_{x \rightarrow \pm x_0}=\pm \infty thì khi đó ta không kết luận được giá trị lớn nhất (hoặc nhỏ nhất) của hàm số đó.
- Nếu đề cho trên một khoảng (a;b), tức là ta sẽ không lấy giá trị ở 2 biên a và b. Vì thế, nếu giá trị lớn nhất (hoặc nhỏ nhất) nằm ở 1 trong 2 biên trên thì đồng nghĩa với việc ta không kết luận được giá trị lớn nhất (hoặc nhỏ nhất) của hàm số đó. Tương tự nếu đề cho (a;b] tức là không lấy giá trị ở biên a hay [a;b) tức là không lấy giá trị ở biên b.
Xem một vài ví dụ dưới đây để hiểu rõ hơn những gì HocThatGioi vừa trình bày ở trên nhé!
Giá trị nhỏ nhất của hàm số y=-x^3+12x+2 trên đoạn [1;4] là:
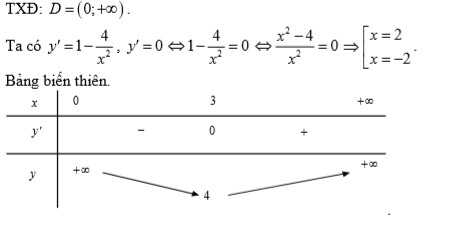
Tìm giá trị nhỏ nhất của hàm số y=x+\frac{4}{x} trên khoảng (4;+\infty)
2. Bài tập tìm giá trị lớn nhất nhỏ nhất của hàm số trên một khoảng, một đoạn
Các bạn hãy bắt tay vào làm ngay các bài tập dưới đây để hiểu rõ và nhớ lâu hơn phương pháp mình vừa giới thiệu ở trên nhé!
Tìm giá trị nhỏ nhất của hàm số y=\frac{2}{3}x^3-\frac{3}{2}x^2-5x+1 trên đoạn [-2;2]
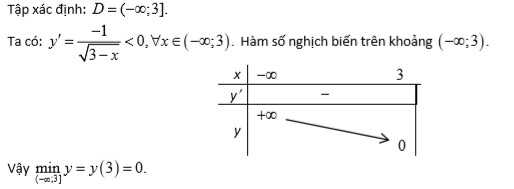
Tìm giá trị nhỏ nhất của hàm số y=2 \sqrt{3-x}
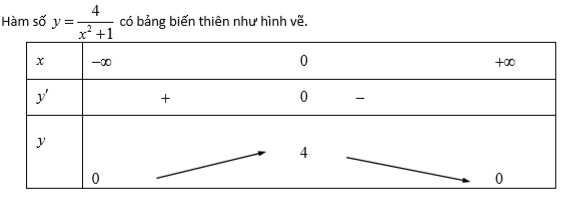
Chọn khẳng định đúng
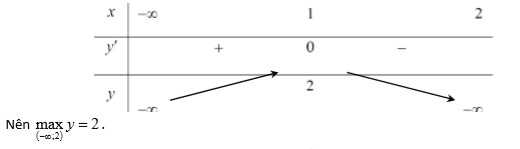
Tìm giá trị lớn nhất của hàm số y=\frac{x^2-3}{x-2} trên khoảng (-\infty;2)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Dạng bài tìm giá trị lớn nhất nhỏ nhất của hàm số trên một khoảng, một đoạn chi tiết. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi nhá. Đừng quên để lại 1 like, 1 cmt để tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!