Khái niệm khối đa diện đầy đủ nhất
Xin chào các bạn, hôm nay chúng ta sẽ bước vào một chuyên đề mới đó là khối đa diện. Trong bài đầu tiên của chuyên đề này chúng ta sẽ nghiên cứu tới khái niệm khối đa diện, hai hình bằng nhau,…. Hãy theo dõi hết bài viết hôm nay cùng HocThatGioi nhé.
1. Khái niệm về hình đa diện và khối đa diện
Dưới đây là khái niệm về hình đa diện và khối đa diện, các bạn hãy theo dõi nhé.
1.1 Khái niệm về hình đa diện
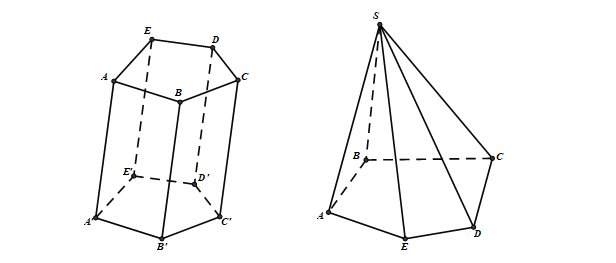
Quan sát hình lăng trụ, hình chóp ở trên ta thấy chúng đều là những hình không gian được tạo bởi một số hữu hạn đa giác. Các đa giác ấy có tính chất
- Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
- Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Mỗi đa giác như thế được gọi là một mặt của hình đa diện (H). Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là các đỉnh, cạnh của hình đa diện (H).
Người ta gọi các hình đó là hình đa diện.
Nói một cách tổng quát: Hình đa diện (gọi tắt là đa diện) (H) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất trên. Mỗi đa giác như thế được gọi là các mặt của đa diện. Các đỉnh các cạnh của đa giác ấy theo thứ tự được gọi là các đỉnh, cạnh của đa diện.
1.2 Khái niệm về khối đa diện
Khối đa diện là phần không gian được giới hạn bới một hình đa diện (H), kể cả hình đa diện đó.
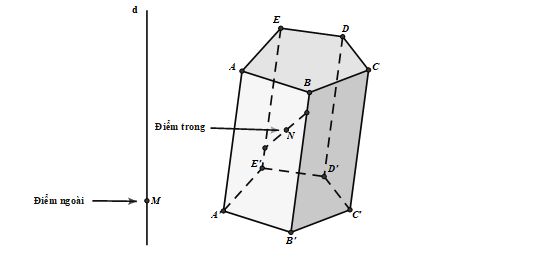
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện.
- Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện
- Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài khối đa diện.
- Mỗi đa diện (H) chia các điểm còn lại của không gian thành hai miền không giao nhau: miền trong và miền ngoài của (H). Trong đó chỉ có duy nhất miền ngoài là chứa hoàn toàn một đường –thẳng d nào đấy.
Khối đa diện (H) là hợp của hình đa diện (H) và miền trong của nó.
2. Hai hình bằng nhau
Sau đây là khái niệm các phép dời hình và khái niệm hai hình bằng nhau
2.1 Phép dời hình trong không gian và sự bằng nhau các khối đa diện
- Trong không gian quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất được gọi là một phép biến hình trong không gian.
- Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
Nhận xét:
- Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
- Phép dời hình biến một đa diện thành (H) một đa diện (H'), biến các đỉnh, cạnh, mặt của đa diện (H) thành đỉnh, cạnh, mặt tương ứng của đa diện (H').
2.1.1 Phép dời hình theo vecto
Là phép biến hình biến điểm M thành M' sao cho \overrightarrow{MM'} = \overrightarrow{v}.
2.1.2 Phép đối xứng qua mặt phẳng (P)
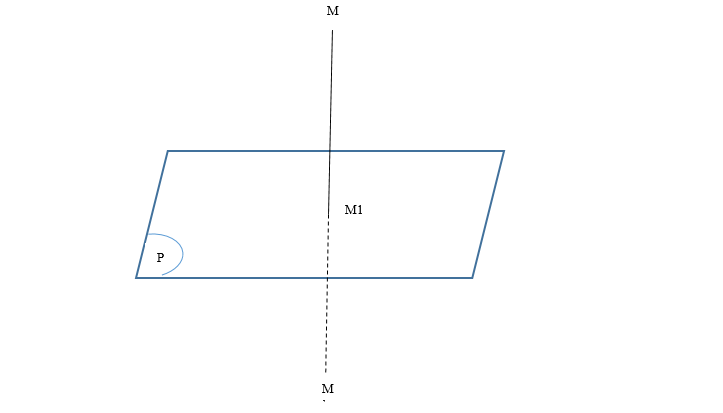
Là phép biến hình biến mọi điểm thuộc (P) thành chính nó, biến điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng chung trực của MM’. Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).
2.1.3 Phép đối xứng tâm O
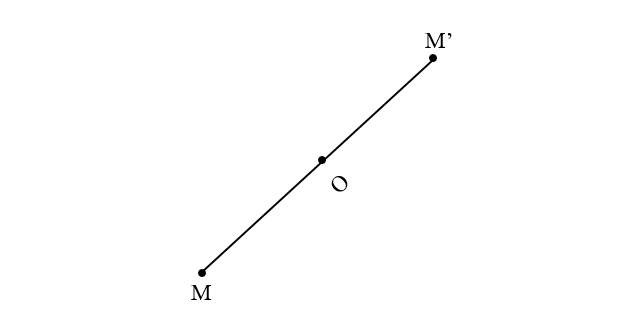
Là phép biến hình biến điểm O thành chính nó, biến điếm M khác O thành điểm M’ sao cho O là trung điểm của MM’. Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).
2.1.4 Phép đối xứng qua đường thẳng d
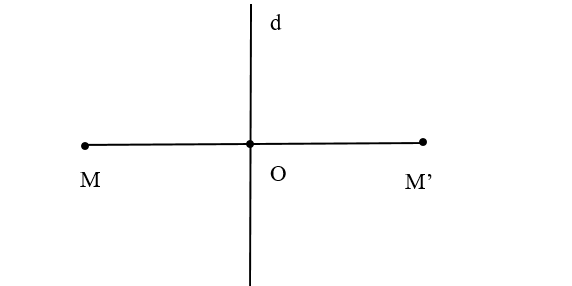
Là phép biến hình mọi điểm thuộc d thành chính nó, biến điểm M không thuộc d thành điểm M’ sao cho d là trung trực của MM’. Phép đối xứng qua đường thẳng d còn được gọi là phép đối xứng qua trục d. Nếu phép đối xứng qua đường thẳng d biến hình (H) thành chính nó thì d được gọi là trục đối xứng của (H).
2.2 Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia
Nhận xét:
- Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình đa diện này thành hình đa diện kia.
- Hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Khái niệm khối đa diện đầy đủ nhất. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Khối đa diện
- Lý thuyết khối đa diện đầy đủ chi tiết nhất
- 20 câu bài tập khối đa diện có lời giải chi tiết nhất
- Phương pháp giải thể tích hình chóp đầy đủ nhất
- 20 câu bài tập tính thể tích hình chóp có lời giải chi tiết nhất
- Phương pháp giải và bài tập tỷ số thể tích đầy đủ nhất
- Công thức và bài tập tính thể tích hình lăng trụ hay nhất
- Công thức thể tích khối đa diện từ cơ bản đến nâng cao cực đầy đủ





