Giải các bài toán Phương trình – Bất phương trình Mũ và Lôgarit bằng casio cực nhanh
Xin chào các bạn, hôm nay HocThatGioi sẽ giới thiệu tới các bạn một phương pháp giải toán hiện đại rất phù hợp trong các kỳ thi. Đó là Giải các bài toán Lôgarit bằng casio cực nhanh. Với phương pháp này các bạn có thể giải quyết dễ dàng và rất nhanh các bài toán. Hãy theo dõi hết bài viết để có thể dùng thành thạo nhé.
1. Giải Phương trình – bất phương trình Mũ và Lôgarit bằng lệnh CALC
Nếu bài toán chỉ hỏi nghiệm thì ta có thể sử dụng lệnh CALC trong máy tính để thử, tuy nhiên bài toán hỏi nghiệm nằm trong khoảng nào, buộc ta phải giải bài toán.
Phương pháp giải:
- Chuyển phương trình – bất phương trình về một vế
- Nhập vào màn hình máy tính casio
- CALC các đáp án và chọn đáp án phù hợp
Ví dụ minh hoạ 1:
Nhấn CALC và cho X = 1 máy tính không tính được. Suy ra loại B và C.
Nhấn CALC và cho X = 5 máy tính không đươc. Loại A
Chọn D

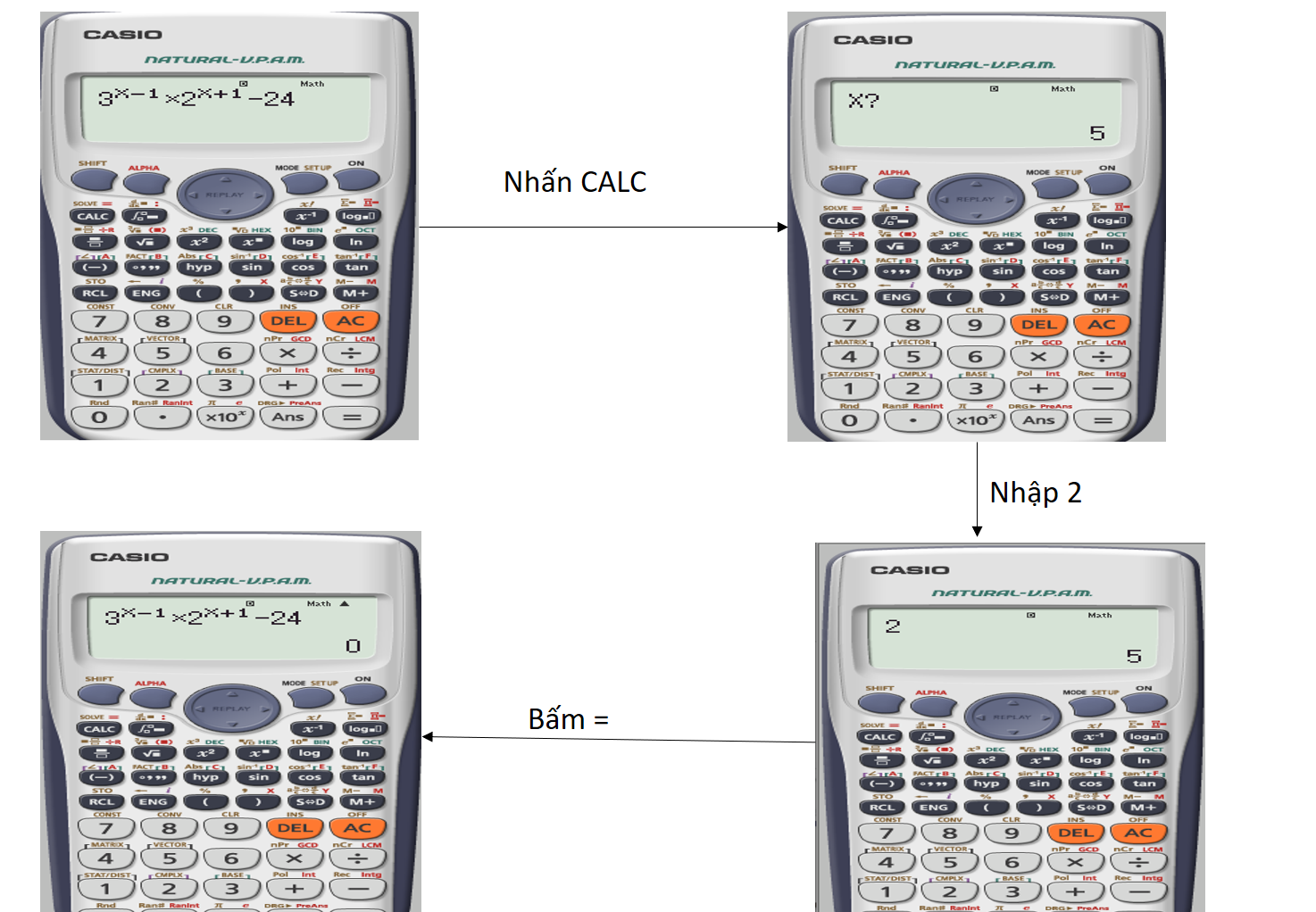
Ví dụ minh hoạ 2:
Khi x = 2 thì giá trị biểu thức bằng 0 nên chọn B
2. Giải Phương trình – bất phương trình Mũ và Lôgarit bằng lệnh TABLE
Nếu bài toán nghiệm thuộc khoảng nào thì lệnh CALC sẽ không dùng được. Vì vậy HocThatGioi sẽ hướng dẫn các bạn dùng lệnh TABLE
Phương pháp giải:
Áp dụng định lý : Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0 thì tồn tại ít nhất một điểm c \in (a;b) sao cho f(c) = 0.
Chức năng của TABLE: lập ra các giá trị của hàm số trong một bảng. Ở đây ta sử dụng TABLE để xem hàm số có đổi dấu trong khoảng cho trước không.
Ví dụ minh hoạ :
F(x) = 2\log_{4}(X^{2} – X) + 3\sqrt{2\log_{4}(X – 1)} – 2\log_{4}X – 4
Ấn hai lần = bỏ qua G(x).
Lúc này máy hiện START ? ấn 1
END? 4
STEP? 0.5 =. Máy sẽ hiện lên như hình dưới. Khi đó ta thấy x = 3 là nghiệm phương trình. Tuy nhiên các bài toán khác ta thấy đổi dấu có thể kết luận có nghiệm. Ở đây ta thấy f(2,5).f(3) < 0 nên có nghiệm

START và END các bạn lấy từ đáp án để nhập
Trên đây là bài viết Giải các bài toán Phương trình – Bất phương trình Mũ và Lôgarit bằng casio cực nhanh mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương Hàm số mũ – Hàm số logarit để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt
Bài viết khác liên quan đến Lớp 12 – Toán – Bất phương trình mũ và bất phương trình logarit
- Phương trình và bất phương trình mũ logarit cơ bản chi tiết nhất
- Phương pháp giải – Bài tập bất phương trình mũ chi tiết nhất
- 15 câu bài tập bất phương trình lôgarit cơ bản có lời giải chi tiết nhất
- 10 câu bài tập Bất phương trình Lôgarit khó có lời giải chi tiết nhất
- 10 câu bài tập bất phương trình mũ khó có lời giải chi tiết nhất
- Phương pháp giải bất phương trình Lôgarit dễ hiểu nhất





