Toán lớp 12
Phương pháp giải và bài tập tỷ số thể tích đầy đủ nhất
Xin chào các bạn, bài viết hôm nay sẽ đem đên cho các bạn một phương pháp giải mới trong bài toán thể tích đó là tỷ số thể tích. Trong bài viết này HocThatGioi sẽ giới thiệu qua phương pháp giải cũng như sẽ có một số bài tập giúp các bạn khái quát được kiến thức. Hãy theo dõi hết bài viết hôm nay nhé.
1. Phương pháp giải tỷ số thể tích
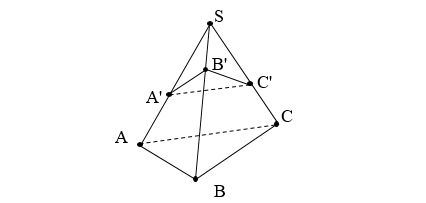
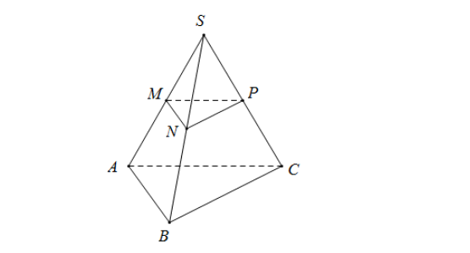
Cho khối chóp S.ABC, A' \in SA, B' \in SB, C' \in SC
Tỷ số thể tích
\frac{V_{S.ABC}}{S.A’B’C’} = \frac{SA.SB.SC}{SA’.SB’.SC’}
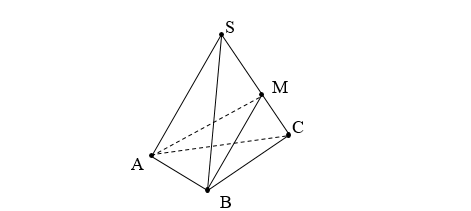
M \in SC, ta có:
Tỷ số thể tích
\frac{V_{SABC}}{V_{SA’B’C’}} = \frac{SA.SB.SM}{SA.SB.SC} = \frac{SM}{SC}
2. Bài tập Tỷ số thể tích
1. Hình chóp S.ABC có A’B’C’ lần lượt là trung điểm của SA, SB, SC; tỷ số thể tích của hai khối chóp SA’B’C’ và SABC là:
2. Cho hàm số S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A’, B’, C’ sao cho SA’ = \frac{1}{2} SA; SB’ = \frac{1}{2} SB; SC’ = \frac{1}{2} SC. Gọi V và V’ lần lượt là thể tích của các khối chóp S.ABCD và S’.A’B’C’. Khi đó tỷ số \frac{V’}{V} là:
3. Cho hình chóp tứ giác đều S.ABCD Gọi A’, B’, C’, D’ theo thứ tự là trung điểm của AB, BC, CD, DA. Khi đó tỉ số thể tích của hai khối chóp S.A’B’C’D’ và S.ABCD bằng ?
4. Hình chóp SABC có M, N, P theo thứ tự là trung điểm SA, SB, SC. Đặt k = \frac{V_{MNPABC}}{SABC}. Khi đó giá trị của k là
5. Cho hình chóp S.ABCD có ABCD là hình bình hành, M là trung điểm SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD lần lượt tại P và Q.Khi đó tỉ số thể tích giữa khối SAPMQ và khối SABCD bằng
6. Cho hình chóp S.ABC, M là trung điểm của SB, điểm N thuộc SC thỏa SN = 2NC. Tỉ số \frac{V_{SAMN}}{V_{S.ABC}}
7. Cho khối tứ diện OABC với OA, OB, OC vuông góc từng đôi một và OA = a, OB = 2a, OC = 3a. Gọi M, N lần lượt là trung điểm của hai cạnh AC, BC. Thể tích của khối tứ diện OCMN tính theo a bằng:
8. Cho hình chóp S.ABCD có thể tích bằng 48 và ABCD là hình thoi. Các điểm M, N, P, Q lần lượt là các điểm trên các đoạn SA, SB, SC, SD thỏa mãn: SA = 2SM, SB = 3SN, SC = 4SP, SD = 5SQ. Tính thể tích khối chóp S.MNPQ
9. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, AC = a\sqrt{2} và SA = a. Gọi G là trọng tâm của tam giác SBC, một mặt phẳng \alpha đi qua AG và song song vsơi BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng
10. Cho khối chóp S.ABC. Lấy A’, B’ lần lượt thuộc SA, SB sao cho 2SA’ = 3A’A; 3SB’ = B’B. Tỉ số thể tích giữa hai khối chóp S.A’B’C và S.ABC là:
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Phương pháp giải và bài tập tỷ số thể tích đầy đủ nhất. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Khối đa diện
- Lý thuyết khối đa diện đầy đủ chi tiết nhất
- Khái niệm khối đa diện đầy đủ nhất
- 20 câu bài tập khối đa diện có lời giải chi tiết nhất
- Phương pháp giải thể tích hình chóp đầy đủ nhất
- 20 câu bài tập tính thể tích hình chóp có lời giải chi tiết nhất
- Công thức và bài tập tính thể tích hình lăng trụ hay nhất
- Công thức thể tích khối đa diện từ cơ bản đến nâng cao cực đầy đủ