Lý thuyết phép đối xứng tâm đầy đủ nhất
Xin chào các bạn, bài viết hôm nay sẽ giới thiệu tới các bạn khái niệm, tính chất,… của Phép đối xứng tâm. Hãy cùng HocThatGioi theo dõi hết bài viết hôm nay nhé.
1. Định nghĩa
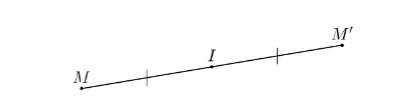
Cho điểm I. Phép biến hình
- Biến điểm I thành chính nó
- Biến mỗi điểm M khác I thành M'
Sao cho I là trung điểm của MM' được gọi là phép đối xứng tâm I.
Điểm I được gọi là tâm đối xứng.
Phép đối xứng tâm I thường được kí hiệu là Đ_{I}
– Nếu hình H’ là ảnh của hình H qua Đ_{I} thì ta nới H đối xứng với H’ qua tâm I, hay H và H’ đối xứng với nhau qua I.
Từ định nghĩa suy ra M’ = Đ_{I}(M) \Leftrightarrow \overrightarrow{IM’} = -\overrightarrow{IM}
– Điêm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến H thành chính nó. Khi đó ta nói H là hình có tâm đối xứng.
2. Tính chất
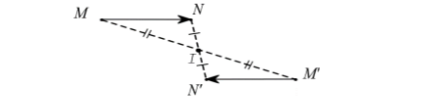
Tính chất 1: Nếu Đ_{I}(M) = M' và Đ_{I}(N) = N' thì \overrightarrow{M'N'} = -\overrightarrow{MN}, từ đó suy ra M'N' = MN
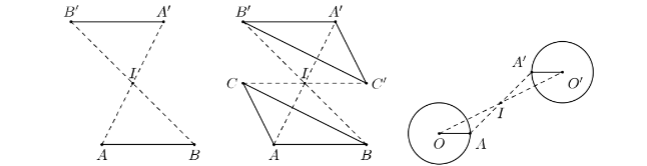
Tính chất 2: Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
3. Biểu thức toạ độ
Trong mặt phẳng Oxy, với mỗi điểm M(x;y), gọi M'(x';y') = Đ_{I}(M).
- Với I = O(0;0), ta có M'(x';y') = Đ_{o}[M(x;y)] thì \left\{\begin{matrix}x' = -x\\y' = -y\end{matrix}\right.
- Với I (a;b), ta có M'(x';y') = Đ_{I}[M(x;y)] thì \left\{\begin{matrix}x' = 2a -x\\y' = 2b - y\end{matrix}\right.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết phép đối xứng tâm đầy đủ nhất. Nếu thấy bài viết này hay, bổ ích hãy chia sẻ ngay đến bạn bè của mình để cùng nhau học giỏi nhé! Chúc các bạn học tốt





