Phương pháp giải các dạng toán phép đối xứng tâm cực hay
Xin chào các bạn, hôm nay HocThatGioi sẽ đem đến cho các bạn những phương pháp để có thẻ giải quyết các dạng toán phép đối xứng tâm. Cũng như một số ví dụ bài tập để các bạn rèn luyên. Hãy theo dõi hết bài viết cùng HocThatGioi nhé.
1. Xác định ảnh của một hình qua phép đối xứng tâm
Phương pháp:
Sử dụng biểu thức toạ độ của phép đối xứng trục.
Trong mặt phẳng Oxy, với mỗi điểm M(x;y), gọi M'(x';y') = Đ_{I}(M).
- Với I = O(0;0), ta có M'(x';y') = Đ_{o}[M(x;y)] thì \left\{\begin{matrix}x' = -x\\y' = -y\end{matrix}\right.
- Với I (a;b), ta có M'(x';y') = Đ_{I}[M(x;y)] thì \left\{\begin{matrix}x' = 2a -x\\y' = 2b - y\end{matrix}\right.
Để tìm tâm đối xứng của một hình ta có nhận xét như sau:
- Nếu hình đã cho là một đa giác thì sử dụng tính chất: Một đa giác có tâm đối xứng I qua phép đối xứng tâm I
- Mỗi đỉnh của nó phải biến thành một đỉnh của đa giác
- Mỗi cạnh của nó phải biến thành một cạnh của đa giác song song và bằng cạnh ấy
- Nếu hình đã cho không phải là một đa giác thì dùng định nghĩa.
Lấy điêm M(x;y) \in d \Rightarrow x + 2y + 3 = 0 (*).
Gọi M'(x’;y’) = Đ_{I}(M) thì \left\{\begin{matrix}x’ = 2 – x\\y’ = 2 – y\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = 2 – x’\\y = 2 – y’\end{matrix}\right.
Thay (*) ta được: (2 – x’) + 2 (2 – y’) + 3 = 0 \Leftrightarrow x’ + 2y’ – 9 = 0.
Vậy ảnh của d là đường thẳng d’: x + 2y – 9 = 0
Cách 2:
Gọi d’ là ảnh của d qua phép đối xứng tâm I, thì d’ song song hoặc trùng với d nên phương trình d’ có dạng x + 2y + c = 0.
Lấy N(-3;0) \in d, gọi N’ = Đ_{I}(N) thì N'(5;2)
Lại có N’ \in d \Rightarrow 5 + 2.2 + c = 0 \Rightarrow c = -9
Vậy d’: x + 2y – 9 = 0
Đường tròn (C) có tâm I(3;-1), bán kính R = 3
Goi I’ là điểm đối xứng của I(3;-1) qua phép đối xứng tâm O(0;0) \Rightarrow I'(-3;1)
Phép đối xứng tâm bảo toàn khoảng cách nên R’ = R = 3
Vậy phương tình đường tròn (C)’ = (x + 3)^{2} + (y – 1)^{2} = 9
Cách 2:
Biểu thức toạ độ của phép đối xứng tâm O(0;0) là \left\{\begin{matrix}x’ = – x\\y’ = – y\end{matrix}\right.
Thay vào (C) ta được (-x’ – 3)^{2} +(-y’ + 1)^{2} = 9 \Leftrightarrow (x’ + 3)^{2} + (y’ – 1)^{2} = 9
2. Xác định tâm đối xứng khi biến ảnh và tạo ảnh
Phương pháp: Sử dụng biểu thức tọa độ và các tính chất của phép đối xứng tâm.
Do phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó nên biến giao điểm A của d với Ox thành giao đểm A’ của d’ với Ox do đó tâm đối xứng là trung điểm của AA’
Vậy tâm đối xứng là I(2;0)
3. Tìm tâm đối xứng của một hình
Phương pháp: Sử dụng biểu thức tọa độ và các tính chất của phép đối xứng tâm.
Gọi I(a;b) là tâm đối xứng của (C) và M(x’;y’) là ảnh của M qua phép đối xứng tâm I
Ta có : \left\{\begin{matrix}x’ = 2a – x\\y’ = 2b – y\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = 2a – x’\\y = 2b – y’\end{matrix}\right.
Thay vào (1) ta được 2b – y’ = (2a – x’)^{3} – 3(2a – x’)^{2} + 3 \Rightarrow y’ = x’^{3} – 3x’^{2} + 3 + (6 – 6a)x’^{2} + (12a^{2} – 12a)x’ – 8a^{3} + 12a^{2} + 2b + 6 (2).
Mặt khác M’ \in (C) nên y’ = x’^{3} – 3x’^{2} + 3 do đó (2) \Leftrightarrow (6 – 6a)x’^{2} + (12a^{2} – 12a)x’ – 8a^{3} + 12a^{2} + 2b – 6 = 0, \forall x’
\left\{\begin{matrix}6 – 6a = 0 \\12a^{2} – 12a = 0\\-8a^{3} + 12a^{2} + 2b – 6 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}a = 1\\b = 1\end{matrix}\right.
Vậy I(1;1) là tâm đối xứng của (C)
4. Sử dụng phép đối xứng tâm để giác các bài toán dựng hình
Phương pháp: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay Đ_{I} nào đó.
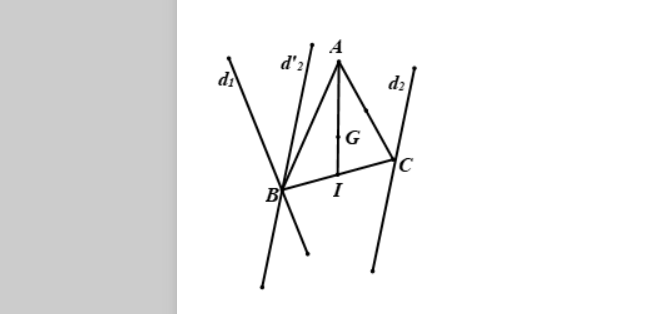
Gỉa sử đã dựng được tam giác ABC thoả mãn yêu cầu bài toán.
Gọi I là trung điẻm BC thì Đ_{I}(C) = B, mà C \in d_{2} nên B \in d_{2}’ với d_{2}’ là ảnh của d_{2} qua phép đối xứng tâm I
Ta lại có B \in d_{1} \Rightarrow B = d_{1} \cap d_{2}’
Cách dựng:
Dựng điểm I sao cho \overrightarrow{AI} = \frac{3}{2}\overrightarrow{AG}
Dựng đường thẳng d_{2}’ ảnh của d_{2} qua Đ_{I}
Gọi B = d_{1} \cap d_{2}’
Dựng điểm C = Đ_{I}(B)
Tam giác ABC là tam giác phải dựng
Chưng minh: Dựa vào cách dựng ta có I là trung điểm BC và \overrightarrow{AI} = \frac{3}{2}\overrightarrow{AG} nên G là trong tâm tam giác ABC
Nhận xét: Số nghiệm hình bằng số giao điểm d_{1} và d_{2}’
5. Sử dụng phép đối xứng tâm để giải bài toán tập hợp điểm
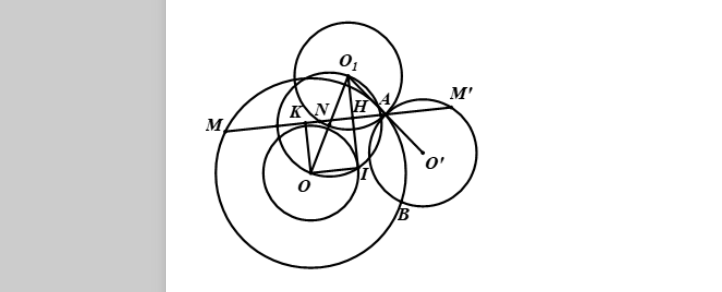
Tương tự IB^{2} = IM.IN
Suy ra IA = IB nên I là trung điểm của AB
Goin P là giao điểm thứ 2 của MN với đường tròn (O)
Dễ thấy P_{I/(O)} = -IM/IP = -IA.IB = -IA^{2}.
Do đó -IM.IN = -IM.IP \Rightarrow IN = IP vậy I là trung điểm của NP. do đó
Đ_{I}(P) = N, mà P di động trên đường tròn (O)
nên N di dộng trên đường tròn (O’) ảnh của đường tròn (O) qua phép đối xứng tâm I.
Vậy tập hợp điểm N là đường tròn (O) qua phép đối xứng tâm I.
Vậy tập hợp điểm N là đường tròn (O’) ảnh của đường tròn (O) qua phép đối xứng tâm I
Như vậy, bài viết về Phương pháp giải các dạng toán phép đối xứng tâm cực hay của HocThatGioi đến đây đã hết. Qua bài viết sẽ giúp các bạn ôn lại các công thức hay gặp trên. Đừng quên Like và Share để HocThatGioi ngày càng phát triển. Cảm ơn các bạn đã theo dõi hết bài viết và chúc các bạn học tốt!





