Giải SGK Bài 3 Chương 6 trang 35, 36, 37, 38, 39, 40, 41 Toán 10 Cánh diều tập 2
Trong bài viết này, HocThatGioi sẽ giải đáp những câu hỏi và bài tập trong bài Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm. Đây là bài học thuộc Bài 3 Chương VI trang 35, 36, 37, 38, 39, 40, 41 sách Toán 10 Cánh diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK Bài 3 Chương 6 Toán 10 Cánh diều tập 2
Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng sẽ giúp bạn dễ dàng tiếp thu kiến thức về Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm.
Câu hỏi khởi động trang 35
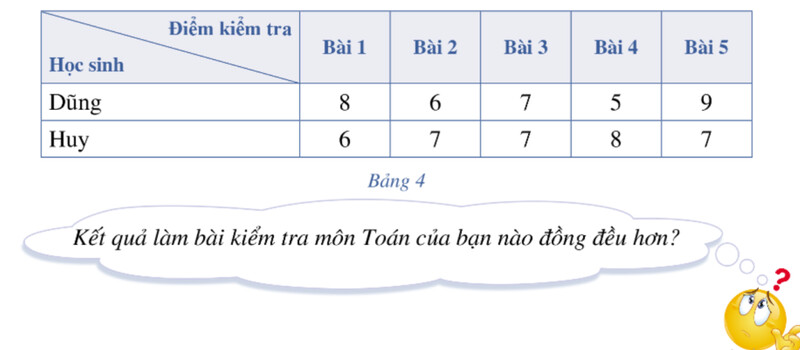
Kết quả kiểm tra Toán của bạn Huy đồng đều hơn, ít chênh lệch hơn.
Hoạt động 2 trang 37
Số trung bình cộng của mẫu số liệu (3) là: \overline{x} = \frac{\mathrm{8+6+7+5+9} }{\mathrm{5} } =7
a) Tính các độ lệch sau: (8 – 7); (6 – 7); (7 – 7); (5 – 7); (9 – 7).
b) Tính bình phương các độ lệch và tính trung bình cộng của chúng.
a) Ta có:
8-7=1; 6-7=-1; 7-7=0; 5-7=-2; 9-7=2
b) Bình phương các độ lệch là:
(8-7)^2 =1; (6-7)^2=1; (7-7)^2=0; (5-7)^2=4; (9-7)^2=4
Trung bình cộng của bình phương các độ lệch là:
s^2= \frac{\mathrm{(8-7)^2 + (6-7)^2+ (7-7)^2+ (5-7)^2+ (9-7)^2} }{\mathrm{5} } =2
Luyện tập vận dụng 1 trang 38
$\begin{array}{lllll}55,2 & 58,8 & 62,4 & 54 & 59,4\end{array}$ (5)
Mẫu số liệu về thời gian (đơn vị: giây) chạy cự li 1500m của 5 người đó là:
$\begin{array}{lllll}271,2 & 261 & 276 & 282 & 270\end{array}$ (6)
Tính phương sai của mẫu (5) và mẫu (6). Từ đó cho biết cự li chạy nào có kết quả đồng đều hơn.
Ta có: \overline{ x_5 } =57,96; \overline{ x_6 } =272,04
Vậy, phương sai của mẫu (5) và mẫu (6) là:
{s_5^2} = \frac{\mathrm{(55,2- \overline{ x_5 })^2+(58,8-\overline{ x_5 })^2+(62,4-\overline{ x_5 })^2+(54-\overline{ x_5 })^2+(59,4-\overline{ x_5 })^2 } }{\mathrm{5} } =9,16
{s_6^2} = \frac{\mathrm{(271,2- \overline{ x_6 })^2+(261-\overline{ x_6 })^2+(276-\overline{ x_6 })^2+(282-\overline{ x_6 })^2+(270\overline{ x_6 })^2 } }{\mathrm{5} } =48,33
Nhận xét: chạy cự ly 500m có kết quả đồng đều hơn.
Hoạt động 3 trang 39
s_H = \sqrt{ {s_H^2} } = \sqrt{0,4} \approx 0,63
Luyện tập vận dụng 2 trang 39
$\begin{array}{lllll}430 & 560 & 450 & 550 & 760 & 430\end{array}$
$\begin{array}{lllll}525 & 410 & 635 & 450 & 800 & 900\end{array}$
Tính độ lệch chuẩn của mẫu số liệu đó
+) Từ số liệu trên, ta có bảng tần số:

s^2= \frac{\mathrm{(410- \overline{x})}^2+(430- \overline{x}) ^2+(450- \overline{x}) ^2+(525-\overline{x}) ^2+(550-\overline{x}) ^2+(560-\overline{x}) ^2+(635-\overline{x}) ^2+(760-\overline{x}) ^2+(800-\overline{x}) ^2+(900-\overline{x}) ^2 }{\mathrm{12}} =25401
+) Độ lệch chuẩn của mẫu số liệu là: s= \sqrt{ s^2 } =159,4
Giải bài tập SGK Bài 3 Chương 6 Toán 10 Cánh diều tập 2
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK Toán 10 Cánh diều tập 2 trang 41 dưới đây nhé.
Bài tập 1 trang 41

b) Tính phương sai của mẫu số liệu thống kê kết quả 5 lần nhảy xa của mỗi bạn. Từ đó cho biết bạn nào có kết quả nhảy xa ổn định hơn.
a) Số trung bình cộng: \overline{x} = \frac{\mathrm{ x_1 + x_2+…+ x_n } }{\mathrm{n} } , so sánh kết quả thu được.
b) Phương sai:
s^2= \frac{\mathrm{1} }{\mathrm{n} } [( x_1 – \overline{x} ) ^2+ ( x_2 – \overline{x} ) ^2+…+( x_n – \overline{x} ) ^2]
Phương sai càng bé thì kết quả càng ổn định
a) Kết quả trung bình của hai bạn bằng nhau: \overline{ x_H } = \overline{ x_T }=2,5 (m )
b) Phương sai mẫu số liệu thống kê của bạn Hùng và Trung là:
{s_H^2} = \frac{\mathrm{(2,4- \overline{ x_H } })^2+(2,6- \overline{ x_H })^2+(2,4-\overline{ x_H })^2+(2,5-\overline{ x_H })^2+(2,6-\overline{ x_H })^2 }{\mathrm{5} } =0,008
{s_T^2} = \frac{\mathrm{(2,4- \overline{ x_T } })^2+(2,5- \overline{ x_T })^2+(2,5-\overline{ x_T })^2+(2,5-\overline{ x_T })^2+(2,6-\overline{ x_T })^2 }{\mathrm{5} } =0,004
Vì 0,004 \lt 0,008 nên ta kết luận: Kết quả chạy xa của bạn Trung ổn định hơn bạn Hùng.
Bài tập 2 trang 41
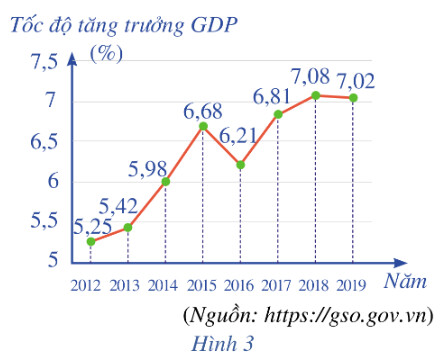
a) Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở Hình 3.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
a) Quan sát biểu đồ
b) Cho mẫu số liệu: x_1, x_2,…x_n
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm X_1, X_2,…X_n
Bước 2: Khoảng biến thiên: R=X_n-X_1
c) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm X_1, X_2,…X_n
Bước 2: Q_2= M_e= \begin{cases} X_{k+1} \\ \frac{\mathrm{1} }{\mathrm{2} } ( X_k+ X_{k+1})\end{cases} \begin{matrix}(n=2k+1)_{}\\(n=2k)_{}\end{matrix}
Q_1 là trung vị của nửa số liệu đã sắp xếp bên trái Q_2 (không bao gồm Q_2 nếu n lẻ)
Q_3 là trung vị của nửa số liệu đã sắp xếp bên phải Q_2 (không bao gồm Q_2 nếu n lẻ)
Khoảng tứ phân vị: \Delta _Q=Q_3-Q_1
d) Tính phương sai:
s^2= \frac{\mathrm{1} }{\mathrm{n} } [( x_1 – \overline{x} ) ^2+ ( x_2 – \overline{x} ) ^2+…+( x_n – \overline{x} ) ^2]
Độ lệch chuẩn: s^2= \sqrt{ s^2 }
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
$\begin{array}{lllll}5,25 & 5,42 & 5,98 & 6,68 & 6,21 & 6,81 & 7,08 & 7,02\end{array}$
b) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
$\begin{array}{lllll}5,25 & 5,42 & 5,98 & 6,21 & 6,68 & 6,81 & 7,02 & 7,08\end{array}$
Khoảng biến thiên của mẫu số liệu đó là: R=x_{max}-x_{min}=7,08-5,25=1,83
c) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
$\begin{array}{lllll}5,25 & 5,42 & 5,98 & 6,21 & 6,68 & 6,81 & 7,02 & 7,08\end{array}$
Các tứ phân vị của mẫu số liệu là: Q_1=5,7; Q_2=6,445; Q_3=7,05
Khoảng tứ phân vị của mẫu số liệu là Q_3-Q_1=1,35
d) Tốc độ tăng trưởng GDP trung bình của Việt Nam giai đoạn 2012-2019 là:
\overline{x} = \frac{\mathrm{5,25+5,42+5,98+6,21+6,68+6,81+7,02+7,08} }{\mathrm{8} } =6,30625 ( \% )
Phương sai của mẫu số liệu là:
s^2= \frac{\mathrm{[(5,25- \overline{x})^2+(5,42- \overline{x})^2 +…+(7,08-\overline{x})^2]} }{\mathrm{8} } \approx 0,44
Độ lệch chuẩn của mẫu số liệu là: s= \sqrt{ s^2 } \approx 0,66( \% )
Bài tập 3 trang 41
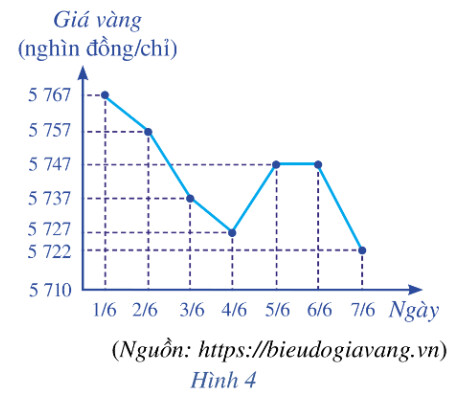
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
a) Quan sát biểu đồ
b) Cho mẫu số liệu: x_1, x_2,…x_n
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm X_1, X_2,…X_n
Bước 2: Khoảng biến thiên: R=X_n-X_1
c) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm X_1, X_2,…X_n
Bước 2: Q_2= M_e= \begin{cases} X_{k+1} \\ \frac{\mathrm{1} }{\mathrm{2} } ( X_k+ X_{k+1})\end{cases} \begin{matrix}(n=2k+1)_{}\\(n=2k)_{}\end{matrix}
Q_1 là trung vị của nửa số liệu đã sắp xếp bên trái Q_2 (không bao gồm Q_2 nếu n lẻ)
Q_3 là trung vị của nửa số liệu đã sắp xếp bên phải Q_2 (không bao gồm Q_2 nếu n lẻ)
Khoảng tứ phân vị: \Delta _Q=Q_3-Q_1
d) Tính phương sai:
s^2= \frac{\mathrm{1} }{\mathrm{n} } [( x_1 – \overline{x} ) ^2+ ( x_2 – \overline{x} ) ^2+…+( x_n – \overline{x} ) ^2]
Độ lệch chuẩn: s^2= \sqrt{ s^2 }
a) Dựa vào biểu đồ, ta có mẫu số liệu là: $\begin{array}{lllll}5767 & 5757 & 5747 & 5737 & 5727 & 5747 & 5747 & 5722\end{array}$
b) Khoảng biến thiên của mẫu số liệu đó là:
R=x_{max}-x_{min}=5767-5722=45
c) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
$\begin{array}{lllll}5722 & 5727 & 5737 & 5747 & 5747 & 5747 & 5757 & 5767\end{array}$
Các tứ phân vị của mẫu số liệu là: Q_1=5732, Q_2=5747, Q_3=5762
Khoảng tứ phân vị của mẫu số liệu là: Q_3-Q_1=30
d) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là:
\overline{x} = \frac{\mathrm{5722+5727+5737+5747+5747+5747+5757+5767} }{\mathrm{8} } = 5743,875 (nghìn đồng/chỉ)
Phương sai của mẫu số liệu là:
$s^2=\frac{\left[(5722-\bar{x})^2+(5727-\bar{x})^2+\ldots+(5767-\bar{x})^2\right]}{8} \approx 193,35$
Độ lệch chuẩn của mẫu số liệu là: s= \sqrt{ s^2 } \approx 13,9 (nghìn đồng/chỉ)
Bài tập 4 trang 41
$\begin{array}{lllll}112 & 102 & 106 & 94 & 101\end{array}$
a) Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.
b) Theo em, các cây có phát triển đồng đều hay không?
a) Số trung bình cộng của mẫu số liệu đã cho là:
$\bar{x}=\frac{112+102+106+94+101}{5}=103 \text {. }$
Phương sai của mẫu số liệu trên là:
$s^2=\frac{(112-103)^2+(102-103)^2+(106-103)^2+(94-103)^2+(101-103)^2}{5}=35,2 $
Độ lệch chuẩn của mẫu số liệu là:
$\mathrm{s}=\sqrt{s^2}=\sqrt{35,2}=\frac{4 \sqrt{55}}{5} \approx 5,93$
b) Vì độ lệch chuẩn của mẫu số liệu là khoảng $5,93$, số này khá lớn, chính vì vậy các cây phát triển không đồng đều.
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài 3 Chương VI trang 35, 36, 37, 38, 39, 40, 41 sách Toán 10 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 10 – Toán – Các số đặc trưng đo xu thế trung tâm
- Giải mục 1 trang 27, 28 SGK Toán 10 Cánh Diều tập 2
- Giải mục 2 trang 28, 29 SGK Toán 10 Cánh diều tập 2
- Giải SGK Bài 2 Chương 6 trang 27, 28, 29, 30, 31, 32, 33, 34 Toán 10 Cánh diều tập 2
- Giải SGK bài 13 chương V trang 78, 79, 80, 81, 82, 83 Toán 10 Kết nối tri thức tập 1
- Giải SGK bài 3 chương VI trang 112, 113, 114, 115, 116, 117, 118, 119 Toán 10 Chân trời sáng tạo tập 1





