Giải SGK bài Toạ độ của Vectơ Toán 10 Cánh diều tập 2
Trong bài viết này, HocThatGioi sẽ giải đáp những câu hỏi và bài tập trong bài Toạ độ của Vectơ. Đây là bài học thuộc Bài 1 Chương VII trang 60, 61, 62, 63, 64, 65, 66 sách Toán 10 Cánh diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Toạ độ của Vectơ Toán 10 Cánh diều tập 2
Dưới đây là lời giải chi tiết cho các câu hỏi hoạt động và luyện tập vận dụng trong bài Toạ độ của Vectơ.
Câu hỏi khởi động trang 60
Toạ độ của vectơ $\overrightarrow{O M}$ là gì?
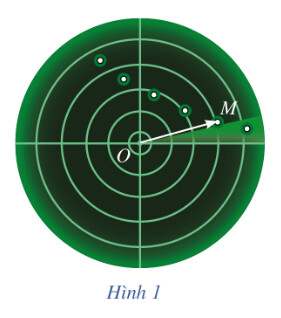
Tọa độ của vectơ $\overrightarrow{O M}$ là tọa độ của điểm M (trong đó O là gốc tọa độ).
Luyện tập vận dụng 1 trang 62
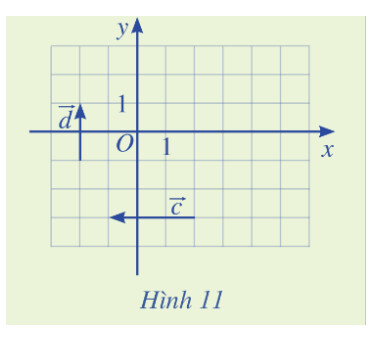
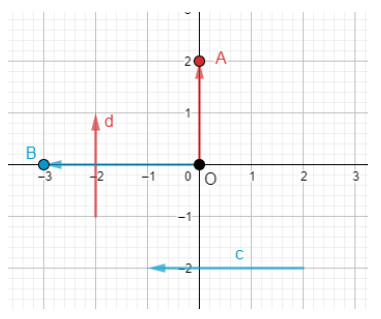
Ta vẽ vectơ $\overrightarrow{O B}=\vec{c}$ và $A(-3 ; 0)$. Tọa độ $\overrightarrow{O B}$ chính là tọa độ của điểm $\mathrm{B}$ nên $\vec{c}=(-3 ; 0)$
Hoạt động 4 trang 63
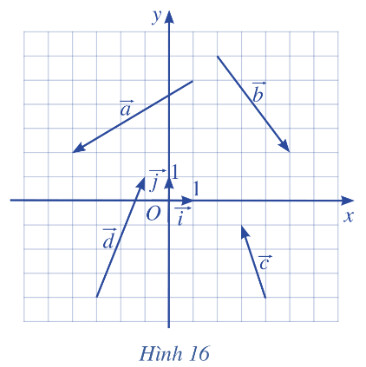
Xét vectơ đơn vị $\vec{i}$ trên trục hoành $O x$ và vectơ đơn vị trên trục tung $O y$ (Hình 12).
a) Tìm hoành độ và tung độ của điểm $A$.
b) Biểu diễn vectơ $\overrightarrow{O H}$ qua vectơ $\vec{i}$.
c) Biểu diễn vectơ $\overrightarrow{O K}$ qua vectơ $\vec{j}$.
d) Chứng tỏ rằng $\vec{u}=a \vec{i}+b \vec{j}$.
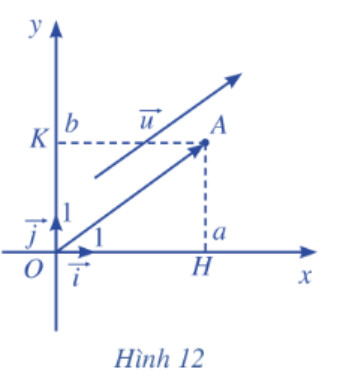
a) Do $\overrightarrow{O A}=\vec{u}$ nên tọa độ vectơ $\overrightarrow{O A}=(a ; b)$. Vậy tọa độ điểm A là: $A(a ; b)$
b) Tọa độ điểm H là $H(a ; 0)$ nên $\overrightarrow{O H}=(a ; 0)$. Do đó, $\overrightarrow{O H}=a \vec{i}$
c) Tọa độ điểm K là $K(0 ; b)$ nên $\overrightarrow{O K}=(0 ; b)$. Do đó, $\overrightarrow{O K}=b \vec{j}$
d) Ta có: $\vec{u}=\overrightarrow{O A}=\overrightarrow{O H}+\overrightarrow{O K}=a \vec{i}+b \vec{j}$ ( ĐPCM )
Luyện tập vận dụng 2 trang 63
a) Biểu diễn vectơ $\vec{v}$ qua hai vectơ $\vec{i}, \vec{j}$
b) Biểu diễn vectơ $\overrightarrow{O B}$ qua hai vectơ $\vec{i}, \vec{j}$
a) Vì $\vec{v}=(0 ;-7)$ nên $\vec{v}=0 \vec{i}+(-7) \vec{j}=-7 \vec{j}$
b) Vì B có tọa độ là $(-1 ; 0)$ nên $\overrightarrow{O B}=(-1 ; 0)$. Do đó: $\overrightarrow{O B}=(-1) \vec{i}+0 \vec{j}=-\vec{i}$
Hoạt động 5 trang 64
a) Tìm hoành độ $x_{A}$ và tung độ $y_{A}$ của điểm $A$; hoành độ $x_{B}$ và tung độ $y_{B}$ của điểm $B$.
b) Tìm điểm $M$ sao cho $\overrightarrow{O M}=\overrightarrow{A B}$. Từ đó, tìm hoành độ $a$ và tung độ $b$ của vectơ $\overrightarrow{A B}$.
c) So sánh: $x_{B}-x_{A}$ và $a ; y_{B}-y_{A}$ và $b$.
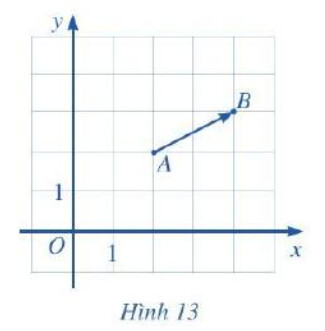
a) Dựa vào hình vẽ, ta có: $x_A=2, y_A=2$ và $x_B=4, y_B=3$
b) Để $\overrightarrow{O M}=\overrightarrow{A B}$ thì điểm $\mathrm{M}$ phải có tọa độ: $M(1 ; 2)$.
Do đó, toạn độ của vectơ $\overrightarrow{A B}$ là $\overrightarrow{A B}=(2 ; 1)$
c) Do $\overrightarrow{A B}=(2 ; 1)$ nên $a=2, b=1$
Ta có: $x_B-x_A=4-2=2, y_B-y_A=3-2=1$
Vậy $x_B-x_A=a$ và $y_B-y_A=b$
Luyện tập vận dụng 3 trang 64
Chứng minh : $\overrightarrow{A B}=\overrightarrow{D C}$
Ta có: $\overrightarrow{A B}=\left(x_B-x_A ; y_B-y_A\right)=(4 ;-4)$ và $\overrightarrow{D C}=\left(x_C-x_D ; y_C-y_D\right)=(4 ;-4)$
Vậy $\overrightarrow{A B}=\overrightarrow{D C}=(4:-4)$
Giải bài tập SGK bài Toạ độ của Vectơ Toán 10 Cánh diều tập 2
Sau khi tìm hiểu các hoạt động đầu mục và phần luyện tập vận dụng, chắc hẳn các bạn cũng đã nắm được kiến thức cơ bản về Toạ độ của Vectơ. Tiếp theo đây, cùng trả lời các câu hỏi trong phần bài tập SGK trang 65, 66 nhé.
Bài tập 1 trang 65
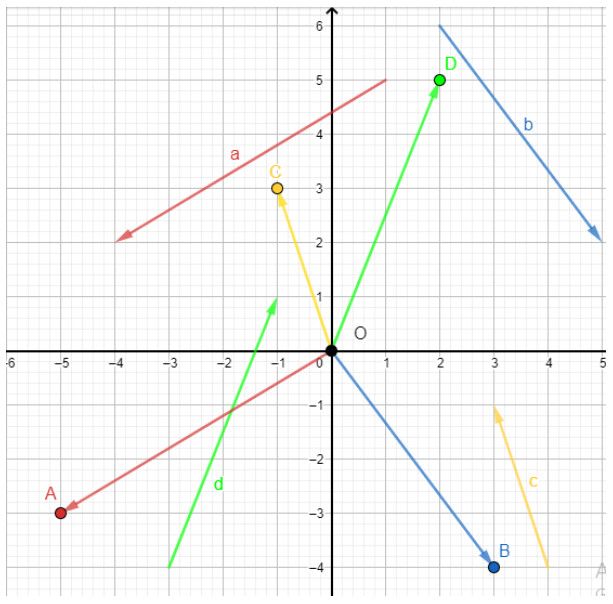
Vẽ các vectơ $\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}, \overrightarrow{O C}=\vec{c}, \overrightarrow{O D}=\vec{d}$.
Tọa độ của 4 điểm $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ là tọa độ của 4 vecto.
Để biểu diễn các vectơ qua vectơ đơn vị: $\vec{u}=(a ; b) \Leftrightarrow \vec{u}=a \vec{i}+b \vec{j}$
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm $A, B, C, D$ là:
$A(-5 ;-3), B(3 ;-4), C(-1 ; 3), D(2 ; 5)$
Do đó $\vec{a}=\overrightarrow{O A}=(-5 ;-3), \vec{b}=\overrightarrow{O B}=(3 ;-4), \vec{c}=\overrightarrow{O C}=(-1 ; 3), \vec{d}=\overrightarrow{O D}=(2 ; 5)$
Vì $\vec{b}=\overrightarrow{O B}=(3 ;-4)$ nên $\vec{b}=3 \vec{i}+(-4) \vec{j}=3 \vec{i}-4 \vec{j}$
Vì $\vec{c}=\overrightarrow{O C}=(-1 ; 3)$ nên $\vec{c}=(-1) \vec{i}+(3) \vec{j}=-\vec{i}+3 \vec{j}$
Vì $\vec{d}=\overrightarrow{O D}=(2 ; 5)$ nên $\vec{d}=2 \vec{i}+5 \vec{j}$
Bài tập 2 trang 65
a) $\vec{a}=3 \vec{i}$
b) $\vec{b}=-\vec{j}$;
c) $\vec{c}=\vec{i}-4 \vec{j}$
d) $\vec{d}=0,5 \vec{i}+\sqrt{6} \vec{j}$.
Sử dụng: $\vec{u}=(a ; b) \Leftrightarrow \vec{u}=a \vec{i}+b \vec{j}$
a) Vì $\vec{a}=3 \vec{i}$ nên $\vec{a}=(3 ; 0)$
b) Vì $\vec{b}=-\vec{j}$ nên $\vec{b}=(0 ;-1)$
c) Vì $\vec{c}=\vec{i}-4 \vec{j}$ nên $\vec{c}=(1 ;-4)$
d) Vì $\vec{d}=0,5 \vec{i}+\sqrt{6} \vec{j}$ nên $\vec{d}=(0,5 ; \sqrt{6})$
Bài tập 3 trang 65
a) $\vec{u}=(2 a-1 ;-3)$ và $\vec{v}=(3 ; 4 b+1)$;
b) $\vec{x}=(a+b ;-2 a+3 b)$ và $\vec{y}=(2 a-3 ; 4 b)$.
Với $\vec{a}=\left(x_1 ; y_1\right)$ và $\vec{b}=\left(x_2, y_2\right)$, ta có: $\vec{a}=\vec{b} \Leftrightarrow\left\{\begin{array}{l}x_1=x_2 \\ y_1=y_2\end{array}\right.$
a) Để $\vec{u}=\vec{v} \Leftrightarrow\left\{\begin{array}{l}2 a-1=3 \\ -3=4 b+1\end{array} \Leftrightarrow\left\{\begin{array}{l}a=2 \\ b=-1\end{array}\right.\right.$
Vậy $\left\{\begin{array}{l}a=2 \\ b=-1\end{array}\right.$ thì $\vec{u}=\vec{v}$
b) $\vec{x}=\vec{y} \Leftrightarrow\left\{\begin{array}{l}a+b=2 a-3 \\ -2 a+3 b=4 b\end{array} \Leftrightarrow\left\{\begin{array}{l}a=1 \\ b=-2\end{array}\right.\right.$
Vậy $\left\{\begin{array}{l}a=1 \\ b=-2\end{array}\right.$ thì $\vec{x}=\vec{y}$
Bài tập 4 trang 66
a) Tìm toạ độ điểm $M$ sao cho $\overrightarrow{A M}=\overrightarrow{B C}$.
b) Tìm toạ độ trung điểm $N$ của đoạn thẳng $A C$. Chứng minh $\overrightarrow{B N}=\overrightarrow{N M}$.
Với $\vec{a}=\left(x_1 ; y_1\right)$ và $\vec{b}=\left(x_2, y_2\right)$, ta có: $\vec{a}=\vec{b} \Leftrightarrow\left\{\begin{array}{l}x_1=x_2 \\ y_1=y_2\end{array}\right.$
a) Gọi $M(a ; b) \Rightarrow \overrightarrow{A M}=(a-2 ; b-3)$
Tọa độ vecto $\overrightarrow{B C}=(4 ;-2)$
Để $\overrightarrow{A M}=\overrightarrow{B C} \Leftrightarrow\left\{\begin{array}{l}a-2=4 \\ b-3=-2\end{array} \Leftrightarrow\left\{\begin{array}{l}a=6 \\ b=1\end{array}\right.\right.$
Vậy để $\overrightarrow{A M}=\overrightarrow{B C}$ thì tọa độ điểm $\mathrm{M}$ là: $M(6 ; 1)$
b) Gọi $N(x, y) \Rightarrow \overrightarrow{N C}=(3-x,-1-y)$ và $\overrightarrow{A N}=(x-2, y-3)$
Do N là trung điểm $\mathrm{AC}$ nên $\overrightarrow{A N}=\overrightarrow{N C}$
$\Leftrightarrow\left\{\begin{array}{l}x-2=3-x \\ y-3=-1-y\end{array} \Leftrightarrow\left\{\begin{array}{l}x=\frac{5}{2} \\ y=1\end{array}\right.\right.$. Vậy $N\left(\frac{5}{2}, 1\right)$
Ta có: $\overrightarrow{B N}=\left(\frac{7}{2} ; 0\right)$ và $\overrightarrow{N M}=\left(\frac{7}{2} ; 0\right)$. Vậy $\overrightarrow{B N}=\overrightarrow{N M}$
Bài tập 5 trang 66
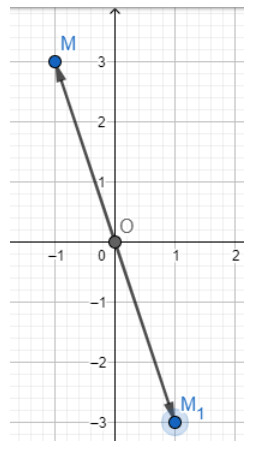
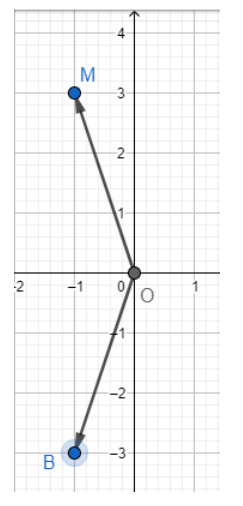
a) Tìm toạ độ điểm $A$ đối xứng với điểm $M$ qua gốc $O$.
b) Tìm toạ độ điểm $B$ đối xứng với điểm $M$ qua trục $O x$.
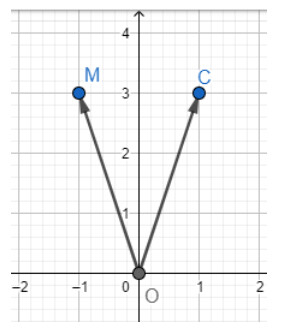
c) Tìm tọa độ điểm $C$ đối xû́ng với điểm $M$ qua trục $O y$.
a) Dựa vào hình vẽ ta thấy $A(1; -3)$
Bài tập 6 trang 66
Tâm đối xứng của hình bình hành là trung điểm hai đường chéo.
Với $\vec{a}=\left(x_1 ; y_1\right)$ và $\vec{b}=\left(x_2, y_2\right)$, ta có: $\vec{a}=\vec{b} \Leftrightarrow\left\{\begin{array}{l}x_1=x_2 \\ y_1=y_2\end{array}\right.$
Gọi $C(a ; b), D(m, n) \Rightarrow \overrightarrow{I C}=(a-4, b-2)$ và $\overrightarrow{I D}=(m-4, n-2)$
Do $I$ là tâm của hình bình hành $A B C D$ nên $I$ là trung điểm $A C$ và $B D$.
Vậy ta có: $\overrightarrow{A I}=\overrightarrow{I C}$ và $\overrightarrow{B I}=\overrightarrow{I D}$
Ta có: $\overrightarrow{A I}=(7 ; 1)$ và $\overrightarrow{B I}=(5 ;-1)$
Do $\overrightarrow{A I}=\overrightarrow{I C} \Leftrightarrow\left\{\begin{array}{l}7=a-4 \\ 1=b-2\end{array} \Leftrightarrow\left\{\begin{array}{l}a=11 \\ b=3\end{array}\right.\right.$.Vậy $C(11 ; 3)$
Do $\overrightarrow{B I}=\overrightarrow{I D} \Leftrightarrow\left\{\begin{array}{l}5=m-4 \\ -1=n-2\end{array} \Leftrightarrow\left\{\begin{array}{l}m=9 \\ n=1\end{array}\right.\right.$. Vậy $D(9 ; 1)$
Bài tập 7 trang 66
Đường trung bình song song và bằng một phần hai cạnh đáy tương ứng
Với $\vec{a}=\left(x_1 ; y_1\right)$ và $\vec{b}=\left(x_2, y_2\right)$, ta có: $\vec{a}=\vec{b} \Leftrightarrow\left\{\begin{array}{l}x_1=x_2 \\ y_1=y_2\end{array}\right.$
Theo tích chất đường trung bình trong một tam giác ta có:
$\overrightarrow{P N}=\overrightarrow{B M}=\overrightarrow{M C}$ và $\overrightarrow{M P}=\overrightarrow{N A}$
Gọi $A\left(a_1, a_2\right), B\left(b_1 ; b_2\right), C\left(c_1 ; c_2\right)$
Ta có: $\overrightarrow{P N}=(2 ; 3), \overrightarrow{B M}=\left(1-b_1 ;-2-b_2\right), \overrightarrow{M C}=\left(c_1-1 ; c_2+2\right), \overrightarrow{M P}=(5 ; 4)$, $\overrightarrow{N A}=\left(a_1-4 ; a_2+1\right)$
Có $\overrightarrow{P N}=\overrightarrow{B M} \Leftrightarrow\left\{\begin{array}{l}2=1-b_1 \\ 3=-2-b_2\end{array} \Leftrightarrow\left\{\begin{array}{l}b_1=-1 \\ b_2=-5\end{array}\right.\right.$.Vậy $B(-1 ;-5)$
Có $\overrightarrow{P N}=\overrightarrow{M C} \Leftrightarrow\left\{\begin{array}{l}2=c_1-1 \\ 3=c_2+2\end{array} \Leftrightarrow\left\{\begin{array}{l}c_1=3 \\ c_2=1\end{array}\right.\right.$.Vậy $C(3 ; 1)$
Có $\overrightarrow{N A}=\overrightarrow{M P} \Leftrightarrow\left\{\begin{array}{l}5=a_1-4 \\ 4=a_2+1\end{array} \Leftrightarrow\left\{\begin{array}{l}a_1=9 \\ a_2=3\end{array}\right.\right.$.Vậy $A(9 ; 3)$
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Giải SGK Bài Toạ độ của Vectơ Chương VII Phương pháp toạ độ trong mặt phẳng trang 60, 61, 62, 63, 64, 65, 66 Toán 10 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!





