SGK Toán 7 – Kết Nối Tri Thức
Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1
Các bài tập cuối chương 4 trang 87 SGK Toán 7 Kết nối tri thức tập 1 sẽ giúp các bạn ôn tập lại các kiến thức về Tam giác bằng nhau một cách chi tiết nhất. Cùng xem HocThatGioi giải quyết các bài toán này nhé!
Bài 4.33 trang 87
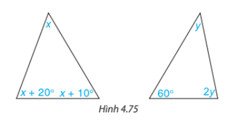
Tính các số đo x, y trong tam giác dưới đây (H.4.75)
Phương pháp giải:
Áp dụng tổng 3 góc của 1 tam giác bằng 180 độ.
Áp dụng tổng 3 góc của 1 tam giác bằng 180 độ.
Lời giải chi tiết:
Áp dụng định lí tổng ba góc trong tam giác,
+) Ta có:
$ x+x+20^{\circ}+x+10^{\circ}=180^{\circ} $
$ \Rightarrow 3 x=150^{\circ} $
$ \Rightarrow x=50^{\circ} $
+) Ta có:
$ y+60^{\circ}+2 y=180^{\circ} $
$ \Rightarrow 3 y=120^{\circ} $
$ y=40^o$
Áp dụng định lí tổng ba góc trong tam giác,
+) Ta có:
$ x+x+20^{\circ}+x+10^{\circ}=180^{\circ} $
$ \Rightarrow 3 x=150^{\circ} $
$ \Rightarrow x=50^{\circ} $
+) Ta có:
$ y+60^{\circ}+2 y=180^{\circ} $
$ \Rightarrow 3 y=120^{\circ} $
$ y=40^o$
Bài 4.34 trang 87
Trong Hình 4.76, có $\mathrm{AM}=\mathrm{BM}, \mathrm{AN}=\mathrm{BN}$. Chứng minh rằng $\widehat{M A N}=\widehat{M B N}$
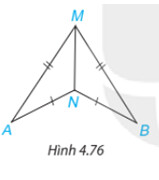
Phương pháp giải:
Chứng minh 2 tam giác $MNA$ và $MNB$ bằng nhau từ đó suy ra 2 góc tương ứng bằng nhau.
Chứng minh 2 tam giác $MNA$ và $MNB$ bằng nhau từ đó suy ra 2 góc tương ứng bằng nhau.
Lời giải chi tiết:
Xét $\triangle M N A$ và $\triangle M N B$ có:
$\mathrm{AM}=\mathrm{BM}$ (gt)
$\mathrm{AN}=\mathrm{BN}$ (gt)
$MN$ chung
$ \Rightarrow \triangle M N A=\triangle M N B \text { (c.c.c) } $
$ =\widehat{M A N}=\widehat{M B N} $(2 góc tương ứng)
Xét $\triangle M N A$ và $\triangle M N B$ có:
$\mathrm{AM}=\mathrm{BM}$ (gt)
$\mathrm{AN}=\mathrm{BN}$ (gt)
$MN$ chung
$ \Rightarrow \triangle M N A=\triangle M N B \text { (c.c.c) } $
$ =\widehat{M A N}=\widehat{M B N} $(2 góc tương ứng)
Bài 4.35 trang 87
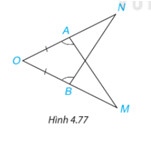
Trong Hình 4.77, có $\mathrm{AO}=\mathrm{BO}, \widehat{O A M}=\widehat{O B N}$. Chứng minh rằng $\mathrm{AM}=\mathrm{BN}$.
Phương pháp giải:
Chứng minh 2 tam giác $OAM$ và $OBN$ bằng nhau từ đó suy ra $AM=BN$.
Chứng minh 2 tam giác $OAM$ và $OBN$ bằng nhau từ đó suy ra $AM=BN$.
Lời giải chi tiết:
Xét 2 tam giác $O A M$ và $O B N$ có:
$ \widehat{O A M}=\widehat{O B N} \text { (gt) } $
$ \mathrm{AO}=\mathrm{BO}(\mathrm{gt}) $
$ \widehat{O} \text { chung } $
$ =>\triangle O A M=\triangle O B N(\mathrm{~g} . \mathrm{c} . \mathrm{g}) $
$ =>\mathrm{AM}=\mathrm{BN} \text { (2 cạnh tương ứng) }$
Xét 2 tam giác $O A M$ và $O B N$ có:
$ \widehat{O A M}=\widehat{O B N} \text { (gt) } $
$ \mathrm{AO}=\mathrm{BO}(\mathrm{gt}) $
$ \widehat{O} \text { chung } $
$ =>\triangle O A M=\triangle O B N(\mathrm{~g} . \mathrm{c} . \mathrm{g}) $
$ =>\mathrm{AM}=\mathrm{BN} \text { (2 cạnh tương ứng) }$
Bài 4.36 trang 87
Trong Hình 4.78 , ta có $\mathrm{AN}=\mathrm{BM}, \widehat{B A N}=\widehat{A B M}$. Chứng minh rằng $\widehat{B A M}=\widehat{A B N}$.
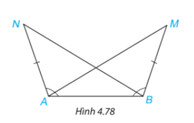
Phương pháp giải:
Chứng minh 2 tam giác $\mathrm{ANB}$ và BMA bằng nhau từ đó suy ra $\widehat{B A M}=\widehat{A B N}$.
Chứng minh 2 tam giác $\mathrm{ANB}$ và BMA bằng nhau từ đó suy ra $\widehat{B A M}=\widehat{A B N}$.
Lời giải chi tiết:
Xét $\triangle A N B$ và $\triangle B M A$ có:
$ \mathrm{AN}=\mathrm{BM} \text { (gt) } $
$ \widehat{B A N}=\widehat{A B M} \text { (gt) }$
$A B$ chung
$ =\triangle A N B=\triangle B M A(\mathrm{c} . \mathrm{g} .\mathrm{c}) $
$ =\widehat{A B N}=\widehat{B A M} \text { (2 góc tương ứng) }$
Xét $\triangle A N B$ và $\triangle B M A$ có:
$ \mathrm{AN}=\mathrm{BM} \text { (gt) } $
$ \widehat{B A N}=\widehat{A B M} \text { (gt) }$
$A B$ chung
$ =\triangle A N B=\triangle B M A(\mathrm{c} . \mathrm{g} .\mathrm{c}) $
$ =\widehat{A B N}=\widehat{B A M} \text { (2 góc tương ứng) }$
Bài 4.37 trang 87
Cho $\mathrm{M}, \mathrm{N}$ là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng $\mathrm{AB}$ sao cho $\mathrm{AM}=\mathrm{AN}$. Chứng minh rằng $\mathrm{MB}=\mathrm{NB}$ và góc $\mathrm{AMB}$ bằng góc $\mathrm{ANB}$.
Lời giải chi tiết:
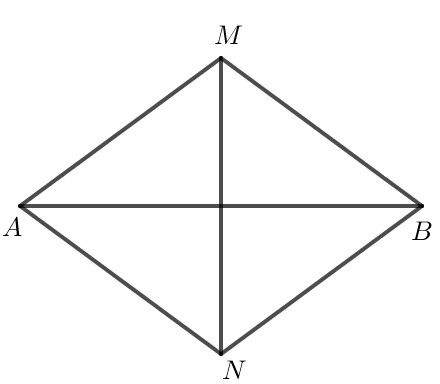
Do $\mathrm{M}$ nằm trên đường trung trực của đoạn thẳng $\mathrm{AB}$ nên $\mathrm{MA}=\mathrm{MB}$.
Do $\mathrm{N}$ nằm trên đường trung trực của đoạn thẳng $\mathrm{AB}$ nên $\mathrm{NA}=\mathrm{NB}$.
Mà $M A=N A$ (theo giải thiết có $A M=A N$ ) nên $M A=M B=N A=N B$.
Suy ra $M B=N B$.
Xét tam giác AMB và tam giác ANB có:
$M A=N A$ (giả thiết)
$\mathrm{MB}=\mathrm{NB}$ (chứng minh trên)
$AB$: cạnh chung
Do đó, $\triangle \mathrm{AMB}=\triangle \mathrm{ANB}(\mathrm{c}-\mathrm{c}-\mathrm{c})$.
Suy ra $\widehat{A M B}=\widehat{A N B}$ (hai góc tương ứng).
Vậy $\mathrm{MB}=\mathrm{NB}$ và $\widehat{A M B}=\widehat{A N B}$.

Do $\mathrm{M}$ nằm trên đường trung trực của đoạn thẳng $\mathrm{AB}$ nên $\mathrm{MA}=\mathrm{MB}$.
Do $\mathrm{N}$ nằm trên đường trung trực của đoạn thẳng $\mathrm{AB}$ nên $\mathrm{NA}=\mathrm{NB}$.
Mà $M A=N A$ (theo giải thiết có $A M=A N$ ) nên $M A=M B=N A=N B$.
Suy ra $M B=N B$.
Xét tam giác AMB và tam giác ANB có:
$M A=N A$ (giả thiết)
$\mathrm{MB}=\mathrm{NB}$ (chứng minh trên)
$AB$: cạnh chung
Do đó, $\triangle \mathrm{AMB}=\triangle \mathrm{ANB}(\mathrm{c}-\mathrm{c}-\mathrm{c})$.
Suy ra $\widehat{A M B}=\widehat{A N B}$ (hai góc tương ứng).
Vậy $\mathrm{MB}=\mathrm{NB}$ và $\widehat{A M B}=\widehat{A N B}$.
Bài 4.38 trang 87
Cho tam giác $A B C$ cân tại $A$ có $\widehat{A}=120^{\circ}$. Trên cạnh $B C$ lấy hai điểm $\mathrm{M}, \mathrm{N}$ sao cho $\mathrm{MA}$, NA lần lượt vuông góc với $A B, A C$. Chứng minh rằng:
a) $\triangle \mathrm{BAM}=\triangle \mathrm{CAN}$;
b) Các tam giác $ANB, AMC$ lần lượt cân tại $N, M$.
a) $\triangle \mathrm{BAM}=\triangle \mathrm{CAN}$;
b) Các tam giác $ANB, AMC$ lần lượt cân tại $N, M$.
Lời giải chi tiết:
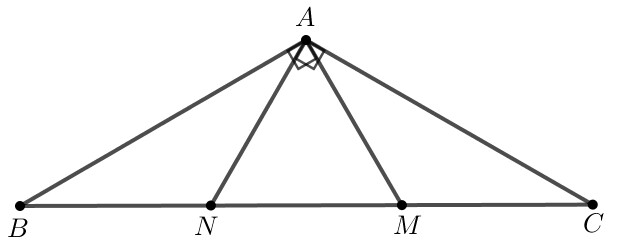
a) Do $M A \perp A B, N A \perp A C$ nên tam giác $BAM$ vuông tại $A$, tam giác $CAN$ vuông tại A.
Do tam giác $\mathrm{ABC}$ cân tại $\mathrm{A}$ nên $\mathrm{AB}=\mathrm{AC}, \widehat{A B C}=\widehat{A C B}$ hay $\widehat{A B M}=\widehat{A C N}$.
Xét hai tam giác $BAM$ vuông tại $\mathrm{A}$ và $\mathrm{CAN}$ vuông tại $\mathrm{A}$ có:
$\widehat{A B M}=\widehat{A C N}$ (chứng minh trên).
$\mathrm{AB}=\mathrm{AC}$ (chứng minh trên).
Vậy $\triangle B A M=\triangle C A N$ (góc nhọn – cạnh góc vuông).
b) Xét tam giác $A B C$ có: $\widehat{A B C}+\widehat{A C B}+\widehat{B A C}=180^{\circ}$.
Mà $\widehat{A B C}=\widehat{A C B}($ do tam giác $A B C$ cân tại $\mathrm{A})$.
Do đó $2 \widehat{A B C}=180^{\circ}-\widehat{B A C}=180^{\circ}-120^{\circ}=60^{\circ}$.
Do đó $\widehat{A B C}=\widehat{A C B}=30^{\circ}$.
Do $\Delta B A M=\triangle C A N$ (chứng minh ởý a) nên $\mathrm{AM}=\mathrm{AN}$ (2 cạnh tương ứng).
Do đó tam giác $AMN$ cân tại A (1).
Xét tam giác CAN vuông tại A có $\widehat{A N C}+\widehat{A C N}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{A N C}=90^{\circ}-\widehat{A C N}=90^{\circ}-30^{\circ}=60^{\circ}$.
Từ (1) và (2) suy ra tam giác $AMN$ đều.
Do đó $\widehat{M A N}=60^{\circ}$.
Ta có: $\widehat{M A N}+\widehat{N A B}=\widehat{M A B}$
Suy ra $\widehat{N A B}=\widehat{M A B}-\widehat{M A N}=90^{\circ}-60^{\circ}=30^{\circ}$.
Do đó $\widehat{N A B}=\widehat{A B N}=30^{\circ}$.
Suy ra tam giác $ANB$ cân tại $N$.
Ta có: $\widehat{M A N}+\widehat{M A C}=\widehat{N A C}$
Suy ra $\widehat{M A C}=\widehat{N A C}-\widehat{M A N}=90^{\circ}-60^{\circ}=30^{\circ}$.
Do đó $\widehat{M A C}=\widehat{M C A}=30^{\circ}$.
Suy ra tam giác $AMC$ cân tại $M$.

a) Do $M A \perp A B, N A \perp A C$ nên tam giác $BAM$ vuông tại $A$, tam giác $CAN$ vuông tại A.
Do tam giác $\mathrm{ABC}$ cân tại $\mathrm{A}$ nên $\mathrm{AB}=\mathrm{AC}, \widehat{A B C}=\widehat{A C B}$ hay $\widehat{A B M}=\widehat{A C N}$.
Xét hai tam giác $BAM$ vuông tại $\mathrm{A}$ và $\mathrm{CAN}$ vuông tại $\mathrm{A}$ có:
$\widehat{A B M}=\widehat{A C N}$ (chứng minh trên).
$\mathrm{AB}=\mathrm{AC}$ (chứng minh trên).
Vậy $\triangle B A M=\triangle C A N$ (góc nhọn – cạnh góc vuông).
b) Xét tam giác $A B C$ có: $\widehat{A B C}+\widehat{A C B}+\widehat{B A C}=180^{\circ}$.
Mà $\widehat{A B C}=\widehat{A C B}($ do tam giác $A B C$ cân tại $\mathrm{A})$.
Do đó $2 \widehat{A B C}=180^{\circ}-\widehat{B A C}=180^{\circ}-120^{\circ}=60^{\circ}$.
Do đó $\widehat{A B C}=\widehat{A C B}=30^{\circ}$.
Do $\Delta B A M=\triangle C A N$ (chứng minh ởý a) nên $\mathrm{AM}=\mathrm{AN}$ (2 cạnh tương ứng).
Do đó tam giác $AMN$ cân tại A (1).
Xét tam giác CAN vuông tại A có $\widehat{A N C}+\widehat{A C N}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{A N C}=90^{\circ}-\widehat{A C N}=90^{\circ}-30^{\circ}=60^{\circ}$.
Từ (1) và (2) suy ra tam giác $AMN$ đều.
Do đó $\widehat{M A N}=60^{\circ}$.
Ta có: $\widehat{M A N}+\widehat{N A B}=\widehat{M A B}$
Suy ra $\widehat{N A B}=\widehat{M A B}-\widehat{M A N}=90^{\circ}-60^{\circ}=30^{\circ}$.
Do đó $\widehat{N A B}=\widehat{A B N}=30^{\circ}$.
Suy ra tam giác $ANB$ cân tại $N$.
Ta có: $\widehat{M A N}+\widehat{M A C}=\widehat{N A C}$
Suy ra $\widehat{M A C}=\widehat{N A C}-\widehat{M A N}=90^{\circ}-60^{\circ}=30^{\circ}$.
Do đó $\widehat{M A C}=\widehat{M C A}=30^{\circ}$.
Suy ra tam giác $AMC$ cân tại $M$.
Bài 4.39 trang 87
Cho tam giác $A B C$ vuông tại $A$ có $B=60^{\circ}$. Trên cạnh $B C$ lấy điểm $\mathrm{M}$ sao cho $\widehat{C A M}=30^{\circ}$. Chứng minh rằng:
a) Tam giác $CAM$ cân tại $M$;
b) Tam giác $BAM$ là tam giác đều;
c) $\mathrm{M}$ là trung điểm của đoạn thẳng $\mathrm{BC}$.
a) Tam giác $CAM$ cân tại $M$;
b) Tam giác $BAM$ là tam giác đều;
c) $\mathrm{M}$ là trung điểm của đoạn thẳng $\mathrm{BC}$.
Lời giải chi tiết:
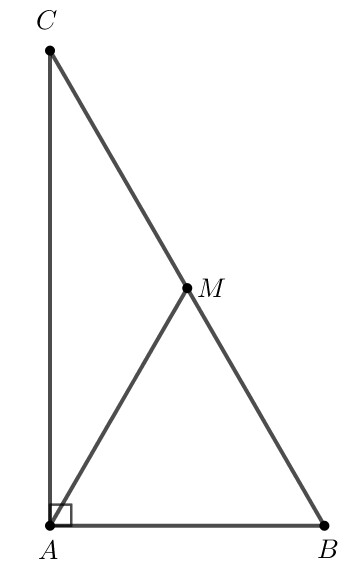
a) Xét tam giác $A B C$ vuông tại $\mathrm{A}$ có $\widehat{A B C}+\widehat{A C B}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{A C B}=90^{\circ}-\widehat{A B C}=90^{\circ}-60^{\circ}=30^{\circ}$.
$\widehat{A C M}=\widehat{A C B}$ nên $\widehat{A C M}=30^{\circ}$.
Tam giác CAM có $\widehat{A C M}=\widehat{C A M}=30^{\circ}$ nên tam giác CAM cân tại $\mathrm{M}$.
Vậy tam giác CAM cân tại $M$.
b) Có $\widehat{B A C}=\widehat{B A M}+\widehat{M A C}$.
Do đó $\widehat{B A M}=\widehat{B A C}-\widehat{M A C}=90^{\circ}-30^{\circ}=60^{\circ}$.
$\widehat{A B M}=\widehat{A B C}$ nên $\widehat{A B M}=60^{\circ}$.
Xét tam giác BAM có $\widehat{A B M}+\widehat{B A M}+\widehat{B M A}=180^{\circ}$.
Do đó
$ \widehat{B M A}=180^{\circ}-\widehat{A B M}-\widehat{B A M} $
$4 =180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$
Tam giác $BAM$ có $\widehat{A B M}=\widehat{B A M}=\widehat{B M A}=60^{\circ}$ nên tam giác $BAM$ là tam giác đều.
Vậy tam giác $BAM$ là tam giác đều.
c) Do tam giác $CAM$ cân tại $M$ nên $MA = MC$ (1).
Do tam giác $BAM$ là tam giác đều nên $M A=M B$ (2).
Từ (1) và (2) ta có $M B = MC$.
Mà $\mathrm{M}$ nằm giữa $\mathrm{B}$ và $\mathrm{C}$ nên $\mathrm{M}$ là trung điểm của $\mathrm{BC}$.
Vậy $M$ là trung điểm của $BC$.

a) Xét tam giác $A B C$ vuông tại $\mathrm{A}$ có $\widehat{A B C}+\widehat{A C B}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{A C B}=90^{\circ}-\widehat{A B C}=90^{\circ}-60^{\circ}=30^{\circ}$.
$\widehat{A C M}=\widehat{A C B}$ nên $\widehat{A C M}=30^{\circ}$.
Tam giác CAM có $\widehat{A C M}=\widehat{C A M}=30^{\circ}$ nên tam giác CAM cân tại $\mathrm{M}$.
Vậy tam giác CAM cân tại $M$.
b) Có $\widehat{B A C}=\widehat{B A M}+\widehat{M A C}$.
Do đó $\widehat{B A M}=\widehat{B A C}-\widehat{M A C}=90^{\circ}-30^{\circ}=60^{\circ}$.
$\widehat{A B M}=\widehat{A B C}$ nên $\widehat{A B M}=60^{\circ}$.
Xét tam giác BAM có $\widehat{A B M}+\widehat{B A M}+\widehat{B M A}=180^{\circ}$.
Do đó
$ \widehat{B M A}=180^{\circ}-\widehat{A B M}-\widehat{B A M} $
$4 =180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$
Tam giác $BAM$ có $\widehat{A B M}=\widehat{B A M}=\widehat{B M A}=60^{\circ}$ nên tam giác $BAM$ là tam giác đều.
Vậy tam giác $BAM$ là tam giác đều.
c) Do tam giác $CAM$ cân tại $M$ nên $MA = MC$ (1).
Do tam giác $BAM$ là tam giác đều nên $M A=M B$ (2).
Từ (1) và (2) ta có $M B = MC$.
Mà $\mathrm{M}$ nằm giữa $\mathrm{B}$ và $\mathrm{C}$ nên $\mathrm{M}$ là trung điểm của $\mathrm{BC}$.
Vậy $M$ là trung điểm của $BC$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương tam giác
- Giải SGK Bài tập cuối chương 7 trang 119, 120 Toán 7 Cánh diều tập 2
- Giải SGK Bài tập cuối chương 8 trang 84 Toán 7 Chân trời sáng tạo tập 2
- Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 9 trang 84 Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung trang 82, 83 SGK Toán 7 Kết nối tri thức Tập 2
- Giải SGK Luyện tập chung trang 86 Toán 7 Kết nối tri thức tập 1
- Giải luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2





