SGK Toán 7 – Kết Nối Tri Thức
Giải SGK bài tập cuối chương 9 trang 84 Toán 7 Kết nối tri thức Tập 2
Sau khi nắm vững các kiến thức lý thuyết, công thức và cách áp dụng chúng để làm bài tập. Hôm nay, hãy cùng HocThatGioi thử sức với các bài tập cuối chương 9 SGK trang 84 ngay nhé. Hy vọng các bạn có thể hoàn thành bài tập của mình thật tốt, trước khi kiểm tra lại đáp án bằng bài viết này nhé!
Giải SGK bài 9.36 trang 84
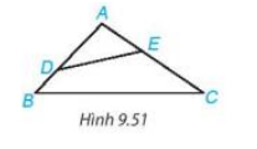
Cho tam giác $ABC$ có $\widehat{BAC}$ là góc tù. Lấy điểm $D$ nằm giữa $A$ và $B$, lấy điểm $E$ nằm giữa $A$ và $C$ (H.9.51). Chứng minh $DE < BC$.
Phương pháp giải:
-Sử dụng tính chất bắc cầu
-Chứng minh $DE < DC$
-Chứng minh $DC < BC$
-Sử dụng tính chất bắc cầu
-Chứng minh $DE < DC$
-Chứng minh $DC < BC$
Lời giải chi tiết:
Ta có: $\widehat{BAC}$ là góc tù nên $\widehat{ADE}$, $\widehat{AED}$ là các góc nhọn.
$\Rightarrow \widehat{DEC}$ là góc tù.
$\Rightarrow DE < DC$ (quan hệ giữa góc và cạnh đối diện trong tam giác $DEC$). $(1)$
Xét tam giác $ADC$ có:
$\widehat{DAC}$ là góc tù nên $\widehat{ADC}, \widehat{ACD}$ là các góc nhọn
$\Rightarrow \widehat{BDC} $là góc tù
$\Rightarrow DC \lt BC$ (quan hệ giữa góc và cạnh đối diện trong tam giác $BDC$) $(2)$
Từ $(1)$ và $(2)$ suy ra: $BC \gt DE$
Ta có: $\widehat{BAC}$ là góc tù nên $\widehat{ADE}$, $\widehat{AED}$ là các góc nhọn.
$\Rightarrow \widehat{DEC}$ là góc tù.
$\Rightarrow DE < DC$ (quan hệ giữa góc và cạnh đối diện trong tam giác $DEC$). $(1)$
Xét tam giác $ADC$ có:
$\widehat{DAC}$ là góc tù nên $\widehat{ADC}, \widehat{ACD}$ là các góc nhọn
$\Rightarrow \widehat{BDC} $là góc tù
$\Rightarrow DC \lt BC$ (quan hệ giữa góc và cạnh đối diện trong tam giác $BDC$) $(2)$
Từ $(1)$ và $(2)$ suy ra: $BC \gt DE$
Giải SGK bài 9.37 trang 84
Cho tam giác $ABC$ ($AB > AC$). Trên đường thẳng chứa cạnh $BC$, lấy điểm $D$ và điểm $E$ sao cho $B$ nằm giữa $D$ và $C$, $C$ nằm giữa $B$ và $E$, $BD = BA$, $CE = CA$ ( H.9.52)
a) So sánh $\widehat{ADE}$ và $\widehat{AED}$
b) So sánh các đoạn thẳng $AD$ và $AE$.
a) So sánh $\widehat{ADE}$ và $\widehat{AED}$
b) So sánh các đoạn thẳng $AD$ và $AE$.

Phương pháp giải:
a) $AB>AC \Rightarrow \widehat{ABC} < \widehat{ACB}$
– Chứng minh.
– $\widehat{ABD} = 180^{\circ} – 2\widehat{ADB}$,
– $\widehat{ACE} = 180^{\circ} – 2\widehat{AEC}$.
b)Sử dụng kết quả câu a)
a) $AB>AC \Rightarrow \widehat{ABC} < \widehat{ACB}$
– Chứng minh.
– $\widehat{ABD} = 180^{\circ} – 2\widehat{ADB}$,
– $\widehat{ACE} = 180^{\circ} – 2\widehat{AEC}$.
b)Sử dụng kết quả câu a)
Lời giải chi tiết:
a) $\Delta$ $ABC$ có $AB > AC$ nên $\Delta$ $ABD$ có $AB = BD$ nên $\Delta$ $ABD$ cân tại $B$.
Khi đó $\widehat{BAD}=\widehat{BDA}$
$\widehat{ABC}$ là góc ngoài tại đỉnh $B$ của $\Delta$ $ABD$ nên $\widehat{ABC} = \widehat{BAD} + \widehat{BDA} = 2\widehat{BDA}$.
$\Delta$ $ACE$ có $AC = CE$ nên $\Delta ACE$ cân tại $C$.
Khi đó $\widehat{CAE} = \widehat{CEA}$
$\widehat{ACB}$ là góc ngoài tại đỉnh $C$ của $\Delta$ $ACE$ nên $\widehat{ACB} = \widehat{CAE} + \widehat{CEA} = 2 \widehat{CEA}$.
Do $\widehat{ACB} > \widehat{ABC}$ nên $2 \widehat{CEA} > 2 \widehat{BDA}$ do đó $\widehat{CEA} > \widehat{BDA}$ hay $\widehat{AED} > \widehat{ADE}$.
b) $\Delta$ $ADE$ có $\widehat{AED}>\widehat{ADE}$ nên $AD > AE$.
a) $\Delta$ $ABC$ có $AB > AC$ nên $\Delta$ $ABD$ có $AB = BD$ nên $\Delta$ $ABD$ cân tại $B$.
Khi đó $\widehat{BAD}=\widehat{BDA}$
$\widehat{ABC}$ là góc ngoài tại đỉnh $B$ của $\Delta$ $ABD$ nên $\widehat{ABC} = \widehat{BAD} + \widehat{BDA} = 2\widehat{BDA}$.
$\Delta$ $ACE$ có $AC = CE$ nên $\Delta ACE$ cân tại $C$.
Khi đó $\widehat{CAE} = \widehat{CEA}$
$\widehat{ACB}$ là góc ngoài tại đỉnh $C$ của $\Delta$ $ACE$ nên $\widehat{ACB} = \widehat{CAE} + \widehat{CEA} = 2 \widehat{CEA}$.
Do $\widehat{ACB} > \widehat{ABC}$ nên $2 \widehat{CEA} > 2 \widehat{BDA}$ do đó $\widehat{CEA} > \widehat{BDA}$ hay $\widehat{AED} > \widehat{ADE}$.
b) $\Delta$ $ADE$ có $\widehat{AED}>\widehat{ADE}$ nên $AD > AE$.
Giải SGK bài 9.38 trang 84
Gọi $AI$ và $AM$ lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh $A$ của tam giác $ABC$. Chứng minh rằng
a) $AI< \frac{1}{2} (AB+AC)$
b) $AM<\frac{1}{2} (AB+AC)$
a) $AI< \frac{1}{2} (AB+AC)$
b) $AM<\frac{1}{2} (AB+AC)$
Phương pháp giải:
a) Sử dụng mối liên hệ giữa đường vuông góc và đường xiên, chứng minh $AI < AB$, $AI < AC$.
b) Lấy $D$ sao cho $M$ là trung điểm của $AD$.
– Chứng minh $AB = CD$.
– Áp dụng bất đẳng thức tam giác cho tam giác $ACD$.
a) Sử dụng mối liên hệ giữa đường vuông góc và đường xiên, chứng minh $AI < AB$, $AI < AC$.
b) Lấy $D$ sao cho $M$ là trung điểm của $AD$.
– Chứng minh $AB = CD$.
– Áp dụng bất đẳng thức tam giác cho tam giác $ACD$.
Lời giải chi tiết:
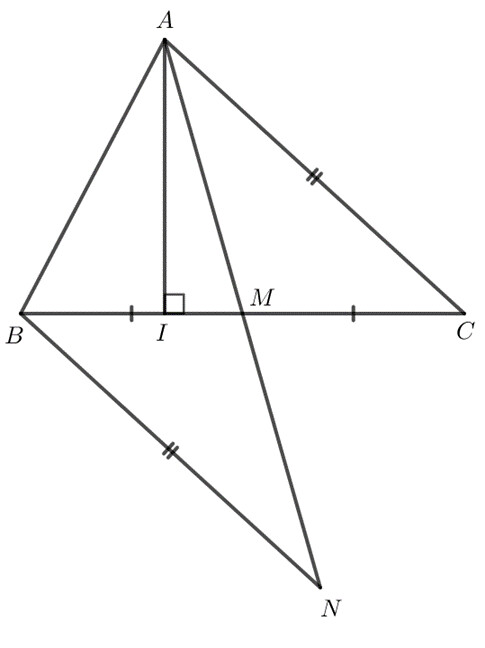
a) $AI$ là đường vuông góc kẻ từ $A$ xuống đoạn thẳng $BC$.
$\Rightarrow \begin{cases} AI \lt AB \\ AI \lt AC \end{cases} $
$\Rightarrow$ $2AI < AB + AC$ (đường vuông góc nhỏ hơn đường xiên)
$\Rightarrow AI < \frac{1}{2}$ $(AB + AC)$.
b)Lấy $D$ sao cho $M$ là trung điểm của $AD$.
Xét $\Delta ABM$ và $DCM$ có
$AM = DM$ (do $M$ là trung điểm của $AD$)
$BM = CM$ (do $M$ là trung điểm của $BC$)
$\widehat{AMB} = \widehat{CMD}$ ($2$ góc đối đỉnh)
$\Rightarrow \Delta ABM = \Delta DCM$ $(c−g−c)$
$\Rightarrow$ $AB = CD$ (2 cạnh tương ứng)
Xét $\Delta ADC$ ta có: $AD < AC + CD$ (bất đẳng thức tam giác)
$\Rightarrow 2AM < AC + AB$
$\Rightarrow AM < \frac{1}{2}(AB + AC$)
$\Rightarrow \begin{cases} AI \lt AB \\ AI \lt AC \end{cases} $
$\Rightarrow$ $2AI < AB + AC$ (đường vuông góc nhỏ hơn đường xiên)
$\Rightarrow AI < \frac{1}{2}$ $(AB + AC)$.
b)Lấy $D$ sao cho $M$ là trung điểm của $AD$.
Xét $\Delta ABM$ và $DCM$ có
$AM = DM$ (do $M$ là trung điểm của $AD$)
$BM = CM$ (do $M$ là trung điểm của $BC$)
$\widehat{AMB} = \widehat{CMD}$ ($2$ góc đối đỉnh)
$\Rightarrow \Delta ABM = \Delta DCM$ $(c−g−c)$
$\Rightarrow$ $AB = CD$ (2 cạnh tương ứng)
Xét $\Delta ADC$ ta có: $AD < AC + CD$ (bất đẳng thức tam giác)
$\Rightarrow 2AM < AC + AB$
$\Rightarrow AM < \frac{1}{2}(AB + AC$)

Giải SGK bài 9.39 trang 84
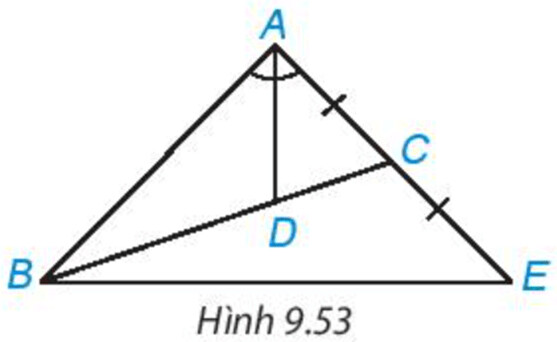
Cho tam giác $ABC$ có đường phân giác $AD$, $D$ nằm trên $BC$ sao cho $BD = 2DC$. Trên đường thẳng $AC$, lấy điểm $E$ sao cho $C$ là trung điểm của $AE$ (H.9.53). Chứng minh rằng tam giác ABE cân tại $A$
Gợi ý $D$ là trọng tâm của tam giác $ABE$, tam giác này có đường phân giác $AD$ đồng thời là trung tuyến.
Gợi ý $D$ là trọng tâm của tam giác $ABE$, tam giác này có đường phân giác $AD$ đồng thời là trung tuyến.
Phương pháp giải:
– $BD = 2DC$, $BC$ là đường trung tuyến từ đó chứng minh được $D$ là trọng tâm tam giác $ABE$.
– $AD$ là phân giác góc $ABE$.
– $BD = 2DC$, $BC$ là đường trung tuyến từ đó chứng minh được $D$ là trọng tâm tam giác $ABE$.
– $AD$ là phân giác góc $ABE$.
Lời giải chi tiết:
$C$ là trung điểm của $AE$
$\Rightarrow $ $BC$ là trung tuyến của tam giác $ABE$ $(1)$
$D$ thuộc $BC$, $BD = 2DC$ $\Rightarrow$
$BD = 2(BC−BD)$ $\Rightarrow$ $3BD = 2BC$ $\Rightarrow$ $BD=$ $\frac{2}{3}BC$ $(2)$
Từ $(1)$ và $(2)$ suy ra: $D$ là trọng tâm của tam giác $ABE$
$\Rightarrow$ $AD$ là đường trung tuyến ứng với $BE$
Mà $AD$ là đường phân giác của $\widehat{BAC}$
$\Rightarrow$ Tam giác $ABE$ cân tại $A$.
$C$ là trung điểm của $AE$
$\Rightarrow $ $BC$ là trung tuyến của tam giác $ABE$ $(1)$
$D$ thuộc $BC$, $BD = 2DC$ $\Rightarrow$
$BD = 2(BC−BD)$ $\Rightarrow$ $3BD = 2BC$ $\Rightarrow$ $BD=$ $\frac{2}{3}BC$ $(2)$
Từ $(1)$ và $(2)$ suy ra: $D$ là trọng tâm của tam giác $ABE$
$\Rightarrow$ $AD$ là đường trung tuyến ứng với $BE$
Mà $AD$ là đường phân giác của $\widehat{BAC}$
$\Rightarrow$ Tam giác $ABE$ cân tại $A$.
Giải SGK bài 9.40 trang 84
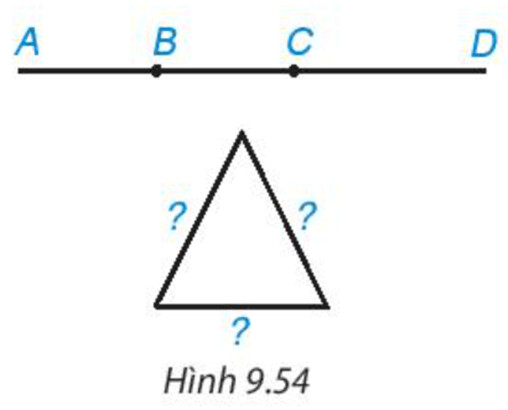
Một sợ dây thép dài $1,2m$. Cần đánh dấu trên sợ dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành tam giác cân có một cạnh bằng $30cm$ (h.9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.
Phương pháp giải:
– Chọn cạnh bên bằng $30 cm$, tính cạnh đáy?
– Chọn cạnh đáy bằng $30 cm$, tính cạnh bên?
– Chọn cạnh bên bằng $30 cm$, tính cạnh đáy?
– Chọn cạnh đáy bằng $30 cm$, tính cạnh bên?
Lời giải chi tiết:
TH1: Cạnh bên bằng $30 cm$
Khi đó cạnh đáy bằng: $120 – (30 + 30 ) =60$ ($cm$)
Vì $30 + 30 = 60$ nên bộ $3$ độ dài này không tạo được thành tam giác.
TH2: Cạnh đáy bằng $30 cm$
Khi đó cạnh bên bằng: $(120 – 30) : 2 = 45$ ($cm$)
Đánh dấu $AB = CD = 45$ $cm$.
TH1: Cạnh bên bằng $30 cm$
Khi đó cạnh đáy bằng: $120 – (30 + 30 ) =60$ ($cm$)
Vì $30 + 30 = 60$ nên bộ $3$ độ dài này không tạo được thành tam giác.
TH2: Cạnh đáy bằng $30 cm$
Khi đó cạnh bên bằng: $(120 – 30) : 2 = 45$ ($cm$)
Đánh dấu $AB = CD = 45$ $cm$.
Vậy là bài Giải SGK bài tập cuối chương 9 trang 84 đã đi đến hồi kết rồi. Các bạn đã hiểu hết những kiến thức và phương pháp mà chúng tớ đã đưa ra chưa? Hy vọng các bạn có thể học tốt và hoành thành xuất sắc bài tập của mình nhé. Hẹn gặp lại bạn ở các bài học sau nhé!!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương tam giác
- Giải SGK Bài tập cuối chương 7 trang 119, 120 Toán 7 Cánh diều tập 2
- Giải SGK Bài tập cuối chương 8 trang 84 Toán 7 Chân trời sáng tạo tập 2
- Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1
- Giải Luyện tập chung trang 82, 83 SGK Toán 7 Kết nối tri thức Tập 2
- Giải SGK Luyện tập chung trang 86 Toán 7 Kết nối tri thức tập 1
- Giải luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2





