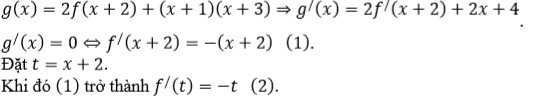Cách giải dạng bài cực trị của hàm hợp, hàm liên kết cực hay

Ngọc Quốc Tháng Bảy 12, 2021

Cách giải chi tiết dạng bài cực trị của hàm hợp hàm liên kết cùng với các ví dụ bám sát dễ hiểu sẽ giúp bạn giải tốt hơn các bài toán dạng này rất nhiều.

Dạng bài cực trị của hàm hợp, hàm liên kết là dạng bài mức độ vận dụng, vận dụng cao của chương cực trị của hàm số. Đây là dạng bài thường gây khó dễ cho các bạn học sinh trong đề thi. Vì thế, trong bài viết này, HocThatGioi sẽ chia sẻ với các bạn cách giải cũng như các bài tập vận dụng về dạng này một cách đầy đủ và chi tiết nhất. Cùng bắt đầu ngay thôi nào.

1. Dạng bài cho giả thuyết về f(x), tìm cực trị của f(u)

Ở dạng bài này, đề thường sẽ cho giả thuyết về $f(x)$ như là đồ thị $f(x)$ , bảng biến thiên $f(x)$ , hàm số $f(x)$ hay là đạo hàm của hàm số $f(x)$ . Và đề sẽ yêu cầu chúng ta phải tìm cực trị của hàm $f(u)$ . Trong đó u là một biểu thức với biến $x$ (ví dụ $x^2, 2x+1,...$ ). Đối với dạng bài này, ta sẽ thực hiện các bước giải lần lượt như sau:

Đạo hàm $(f(u))'=f'(u).u'$
Tìm nghiệm của biểu thức vừa đạo hàm: $f'(u)=0$ hoặc $u'=0$ . Các nghiệm này thường không phải là nghiệm chính xác mà là các giá trị nghiệm tương đối.
Xét các nghiệm vừa tìm được là nghiệm bội chẵn (không phải cực trị) hay nghiệm bội lẻ (là cực trị). Cũng có thể vẽ BBT để biểu thị rõ hơn.
Kết luận

Nếu bạn vẫn chưa hiểu rõ về các bước mà mình vừa chia sẻ ở trên thì hãy xem ví dụ sau đây nhé, sẽ giúp các bạn hiểu hơn nhiều đấy!

Cho hàm số $y=f(x)$ như hình bên dưới, tìm số cực trị của hàm số $y=f(x^2)$

Cách giải dạng bài cực trị của hàm hợp, hàm liên kết cực hay 6

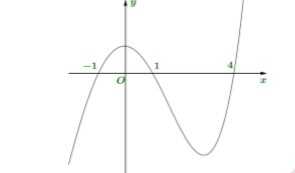
2. Dạng bài tìm cực trị của h(x) = f(u) + g(x)

Ở dạng bài này, đề thường sẽ cho đồ thị của hàm $f'(x)$ và yêu cầu tìm cực trị của hàm $h(x)=f(u)+g(x)$ (ví dụ $f(x+1) -3x, f(3-x) +2x^2+1$ ). Đối với dạng bài này, ta sẽ giải lần lượt các bước sau đây:

Đạo hàm: $h'(x)=f'(u).u'+g'(x)$
Đặt t=u, rút x theo t và sau đó chuyển biểu thức biến x thành biểu thức biến t.
Rút $f'(t)=z(t)$ . Dựa vào đồ thị của $f'(x)$ , ta coi như đó là đồ thị của $f'(t)$ và sau đó vẽ đè $z(t)$ lên đồ thị.
Từ đó, tìm các giá trị của t là giao điểm của 2 đồ thị $f'(t)$ và $z(t)$ , từ đó suy ra các giá trị của x.
Vẽ BBT của $h(x)$ và rút ra kết luận

Xem ngay ví dụ sau đây nếu bạn vẫn còn đang cảm thấy mơ hồ về cách giải dạng này nhé!

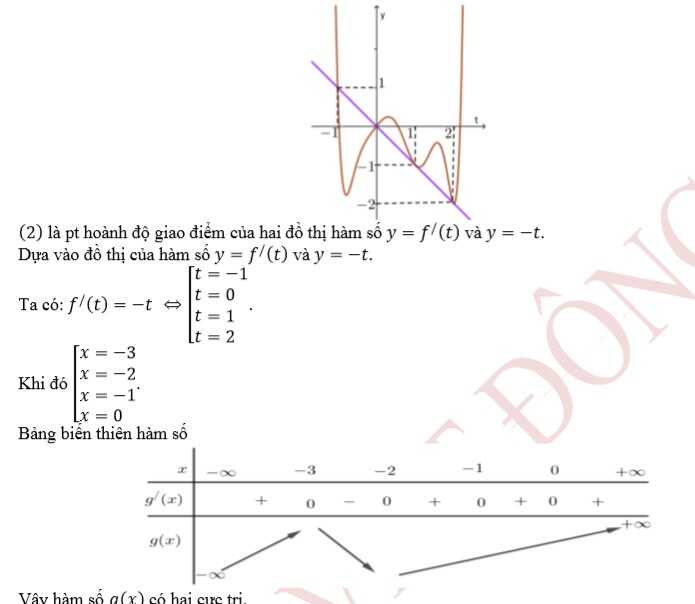
Cho hàm số $y=f(x)$ và xác định trên R. Đồ thị hàm số y=f'(x) như hình bên.Tìm số cực trị của hàm số $g(x) = 2 f (x+2) + (x+1)(x+3)$ .

Cách giải dạng bài cực trị của hàm hợp, hàm liên kết cực hay 8

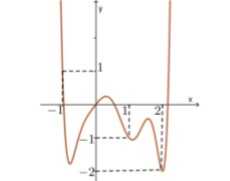
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Dạng bài cực trị của hàm hợp, hàm liên kết cực hay. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi nhá. Đừng quên để lại 1 like, 1 cmt để tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!