2 dạng bài nâng cao về cực trị của hàm số – đường thẳng cực trị và tam giác cực trị
Dạng bài đường thẳng cực trị và tam giác cực trị khá phổ biến trong đề thi - Lý thuyết cơ bản và cách giải cực hay và chi tiết
Hai dạng bài đường thẳng cực trị và tam giác cực trị là các dạng bài đặc biệt và tương đối khó trong chương cực trị của hàm số. Bài viết ngày hôm nay, HocThatGioi sẽ chia sẻ cho các bạn những kiến thức quan trọng cũng như phương pháp giải 2 dạng bày này. Cùng với đó là các bài tập rất hay giúp các bạn rèn luyện nữa đấy!
1. Dạng bài về đường thẳng nối 2 điểm cực trị
1.1 Đường thẳng nối 2 điểm cực trị là gì?
Đường thẳng nối 2 điểm cực trị là đường thẳng đi qua hai cực trị của hàm số bậc ba, để tìm đường thẳng đi qua 2 cực trị của hàm số bậc 3, ta có thể thực hiện 1 trong 2 cách sau:
- Cách 1: Giả sử hàm số đi qua 2 điểm cực trị A(x_1,y_1), B(x_2,y_2) thì đường thẳng cực trị sẽ dễ dạng tìm được bằng cách viết phương trình đường thẳng AB.
- Cách 2: Chia đa thức f(x) cho f'(x)
1.2 Cách giải dạng bài đường thẳng nối 2 điểm cực trị
Các bước giải dạng bài đường thẳng nối 2 điểm cực trị cần phải nắm
- Xác định đường thẳng cực trị
- Giải quyết yêu cầu của bài toán về đường thẳng cực trị
- Kết luận
Dạng bài về đường thẳng nối 2 điểm cực trị khá phong phú, mỗi dạng sẽ có cách giải quyết khác nhau, ta cần phải linh động thì mới có thể giải tốt dạng bài này. Xem các ví dụ dưới đây để hiểu rõ hơn nhé!
Tìm giá trị thực của tham số m để đường thẳng y=(2m-1)x-3-m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y=x^3-3x^2+1
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số y=\frac{1}{3}x^3-mx^2+(m^2-1)x có hai điểm cực trị A và B sao cho A B, nằm khác phía và cách đều đường thẳng d : y=5x-9 Tính tổng tất cả các phần tử của S .
Nếu các bạn đã hiểu rõ về các ví dụ trên thì hãy thử sức với các bài tập dưới đây nhé!
Cho hàm số y=\frac{1}{3}mx^3-(m-1)x^2+(3m-2)x+2018 với m là tham số. Tổng bình phương tất cả các giá trị của m để hàm số có hai điểm cực trị x_1,x_2 thoả x_1+2x_2=1 là ?
Tìm tất cả giá trị của tham số m để hàm số y=x^3-3x^2+mx-1 đạt cực trị tại x_1,x_2 để x_1^2+x_2^2=6 ?
2. Dạng bài về tam giác cực trị
2.1 Tam giác cực trị là gì?
- A luôn nằm trên trục tung (tức hoành độ của A luôn bằng 0)
- Tam giác ABC là tam giác cân tại A
- B và C đối xứng nhau qua trục tung (trục Oy)
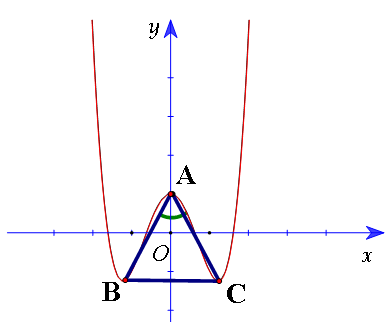
Công thức tìm nhanh tọa độ của các điểm trong tam giác cực trị:
- A(0;c)
- B(-\sqrt {-\frac{b}{2a}};\frac{-\Delta}{4a})
- C(\sqrt {-\frac{b}{2a}};\frac{-\Delta}{4a})
2.2 Cách giải dạng bài tam giác cực trị
Dạng bài về tam giác cực trị này rất đa dạng, muôn vàng muôn kiểu. Tuy nhiên chỉ cần bạn nắm được bản chất của nó là có thể giải rất dễ dàng luôn đấy!
- Tìm tọa độ các điểm của tam giác cực trị
- Tìm điều kiện để tam giác cực trị thỏa yêu cầu đề bài
- Kết luận
Tham khảo các ví dụ dưới đây để hiểu rõ hơn về dạng bài này nhé!
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y=x^4-2mx^2 có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1
Cho hàm số y=x^4-2mx^2+1 Tổng lập phương các giá trị của tham số m để đồ thị hàm số có ba điểm cực trị và đường tròn đi qua 3 điểm này có bán kính R=1 bằng
Thử sức với các bài tập dưới đây xem các bạn đã hiểu tới đâu nhé!
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=x^4-2m^2x^2+m+4 có ba điểm cực trị tạo thành ba đỉnh của một tam giác
đều?
Tìm m để đồ thị hàm số y=x^4-2m^2x^2+m+4 có 3 điểm cực trị lập thành một tam giác vuông cân
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Tổng hợp các dạng bài từ cơ bản đến nâng cao về cực trị của hàm số. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Cực trị của hàm số
- Cực trị của hàm số – Lý thuyết và các dạng bài thường gặp đầy đủ chi tiết nhất
- Cực trị của các hàm số cơ bản hay gặp nhất trong đề thi
- Lý thuyết và cách giải cực trị của các hàm số nâng cao cực hay
- Dạng bài tìm tham số sao cho cực trị của hàm số thỏa điều kiện cho trước cực chi tiết
- Dạng bài tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của f(x) f'(x) cực hay
- Tổng hợp tài liệu về cực trị của hàm số cực hữu ích
- Cách giải dạng bài cực trị của hàm hợp, hàm liên kết cực hay








