Giải Luyện tập chung Chương 7 trang 44, 45 SGK Toán 7 Kết nối tri thức Tập 2
Ở bài viết này, HocThatGioi sẽ cùng củng cố lại những kiến thức đã học ở chương 7. Bằng cách vận dụng những công thức, lý thuyết đã học. Để giải tất cả các bài tập ở phần Luyện tập chung Chương 7 SGK Trang 44, 45 Toán 7 Kết nối tri thức tập 2. Hy vọng, sau bài viết này các bạn có thể nắm vững những kiến thức mình đã học qua. Và có thể áp dụng chúng một cách dễ dàng theo những lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải bài 7.36 SGK trang 45
$(5x^{3} – 4x^{2}) : 2^{2} + (3^{4} + 6x) : 3x – x(x^{2} – 1)$
+) Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
+) Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau
$(5x^{3} – 4x^{2}) : 2x^{2} + (3x^{4} + 6x) : 3x – x(x^{2} – 1)$
$= 5x^{3} : 2x^{2} + (-4x^{2}): 2x^{2} + 3x^{4} : 3x + 6x : 3x – [x. x^{2} + x . (-1)]$
$= (5:2). (x^{3} : x^{2}) + [(-4) : 2]. (x^{2} : x^{2}) + (3 : 3). (x^{4} : x) + (6 : 3). (x:x) – ( x^{3} – x)$
$= \frac{5}{2}x – 2 + x^{3} + 2 – x^{3} + x$
$= (x^{3} – x^{3}) + (\frac{5}{2}x + x) + (-2 + 2)$
$= 0 + \frac{7}{2}x + 0$
$= \frac{7}{2}x$
Giải bài 7.37 SGK trang 45
a) $2x(x+3) – 3x^{2}(x+2) + x(3x^{2} + 4x – 6)$
b) $3x(2x^{2} – x) – 2x^{2}(3x+1) + 5(x^{2} – 1)$
Bước $1$: Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
Bước $2$: Cộng, trừ các đa thức thu được
a) $2x(x+3) – 3x^{2}(x+2) + x(3x^{2} + 4x – 6)$
$= (2x . x + 2x . 3) – (3x^{2} . x + 3x^{2} . 2) + (x . 3x^{2} + x . 4x – x . 6)$
$= 2x^{2} + 6x – (3x^{3} + 6x^{2}) + (3x^{3} + 4x^{2} – 6x)$
$= 2x^{2} + 6x – 3x^{3} – 6x^{2} + 3x^{3} + 4x^{2} – 6x$
$= (– 3x^{3} + 3x^{3} ) + (2x^{2} – 6x^{2} + 4x^{2} ) + (6x – 6x)$
$= 0 + 0 + 0$
$= 0$
b) $3x(2x^{2} – x) – 2x^{2}(3x+1) + 5(x^{2} – 1)$
$= [3x . 2x^{2} + 3x . (-x)] – (2x^{2} . 3x + 2x^{2} . 1) + [5x^{2} + 5 . (-1)]$
$= 6x^{3} – 3x^{2} – (6x^{3} +2x^{2}) + 5x^{2} – 5$
$= 6x^{3} – 3x^{2} – 6x^{3} – 2x^{2} + 5x^{2} – 5$
$= (6x^{3}– 6x^{3} ) + (-3x^{2} – 2x^{2}+ 5x^{2}) – 5$
$= 0 + 0 – 5$
$= – 5$
Giải bài 7.38 SGK trang 45
a) $3x^{2} – 3x(x – 2) = 36$
b) $5x(4x^{2} – 2x + 1) – 2x(10x^{2} – 5x + 2) = -36$
Rút gọn đa thức ở vế trái để đưa về bài toán tìm x quen thuộc.
a)3x^{2}−3x(x−2)=36
$\Leftrightarrow 3x^{2}−[3x.x+3x.(−2)]=36$
$\Leftrightarrow 3x^{2}−(3x^{2}−6x)=36$
$\Leftrightarrow 3x^{2}−3x^{2}+6x=36$
$\Leftrightarrow 6x=36 $
$\Leftrightarrow x=36:6$
$\Leftrightarrow x=6$
Vậy $x = 6$
b)$5x(4x^{2}−2x+1)−2x(10x^{2}−5x+2)=−36 $
$\Leftrightarrow 5x.4x^{2}+5x.(−2x)+5x.1−[2x.10x^{2}+2x.(−5x)+2x.2]=−36 $
$\Leftrightarrow 20x^{3}−10x^{2}+5x−(20x^{3}−10x^{2}+4x)=−36 $
$\Leftrightarrow 20x^{3}−10x^{2}+5x−20x^{3}+10x^{2}−4x=−36 $
$\Leftrightarrow (20x^{3}−20x^{3})+(−10x^{2}+10x^{2})+(5x−4x)=−36 $
$\Leftrightarrow x=−36$
Vậy $x = -36$
Giải bài 7.39 SGK trang 45
a) $(x^{3} – 8) : (x – 2)$
b) $(x – 1)(x + 1)(x^{2} + 1)$
+) Muốn chia đa thức $A$ cho đa thức $B$, ta làm như sau:
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $A$ chia cho hạng tử bậc cao nhất của $B$.
Bước $2$: Lấy $A$ trừ đi tích của $B$ với thương mới thu được ở bước $1$.
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $B$.
Bước $4$: Lấy dư thứ nhất trừ đi tích $B$ với thương vừa thu được ở bước $3$
Bước $5$: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của $B$ thì quá trình chia kết thúc.
+) Nhân các đa thức:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau
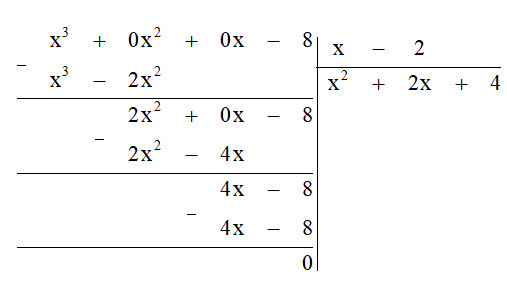
b) $(x – 1)(x + 1)(x^{2} + 1)$
$= [x .(x + 1) – 1 .(x + 1)] . (x^{2} + 1)$
$= {x.x + x.1 + (-1).x + (-1).1}. (x^{2} + 1)$
$= (x^{2} + x – x – 1) . (x^{2} + 1)$
$= (x^{2} – 1) . (x^{2} + 1)$
$= x^{2} . (x^{2} +1) – 1.(x^{2} + 1)$
$= x^{2} . x^{2} + x^{2} . 1 – (1.x^{2} + 1.1)$
$= x^{4} + x^{2} – (x^{2} + 1)$
$= x^{4} + x^{2} – x^{2} – 1$
$= x^{4} – 1$
Giải bài 7.40 SGK trang 45
$P(x) = x^{2} (7x – 5) – (28x^{5} – 20x^{4} – 12x^{3}) : 4x^{2}$
Luật chơi là sau khi chủ trò đọc một số a nào đó, các đội chơi phải tìm giá trị của $P(x)$ tại $x = a$. Đội nào tính đúng và tính nhanh nhất thì thắng cuộc.
Khi chủ trò vừa đọc $a = 5$, Vuông đã tính ngay được $P(a) = 15$ và thắng cuộc. Em có biết Vuông làm cách nào không?
Bước $1$: Rút gọn biểu thức
Bước $2$: Thay giá trị của x mà chủ trò đọc vào biểu thức vừa rút gọn và tính giá trị biểu thức
$P(x) = x^{2} (7x – 5) – (28x^{5}– 20x^{4} – 12x^{3}) : 4x^{2}$
$= x^{2} . 7x – x^{2} . 5 – ( 28x^{5} : 4x^{2} – 20x^{4} : 4x^{2} – 12x^{3} : 4x^{2})$
$= 7x^{3} – 5x^{2} – (7x^{3} – 5x^{2} – 3x)$
$= 7x^{3} – 5x^{2} – 7x^{3} + 5x^{2} +3x$
$= (7x^{3} – 7x^{2} ) + (– 5x^{2} + 5x^{2} ) + 3x$
$= 0 +0 + 3x$
$=3x$
Khi $x = 5$ thì $P(5) = 3.5 =15$
Vậy Vuông chỉ cần rút gọn biểu thức $P(x)$, sau đó thay $x = 5$ vào $P(x)$ đã rút gọn
Giải bài 7.41 SGK trang 45
Thực hiện phép chia đa thức cho đa thức.
Để $A$ chia hết cho $B$ thì số dư $= 0$.
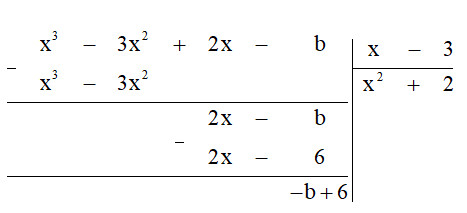
Bài giải hôm nay đến đây đã kết thúc. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải Luyện tập chung trang 44, 45 Chương 7 SGK Toán 7 Kết nối tri thức Tập 2. Hi vọng các bạn có thể hiếu hết tất cả các bài tập mà chúng tớ đã trình bày nhé. Chúc các bạn có một buổi học thật thú vị và nhiều kiến thức hay nhé. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương biểu thức đại số
- Giải SGK Bài tập cuối chương 6 trang 68, 69 Toán 7 Cánh diều tập 2
- Giải SGK bài tập cuối chương 7 Toán 7 Chân trời sáng tạo Tập 2
- Giải SGK bài tập cuối chương VI Toán 7 Chân trời sáng tạo Tập 2
- Giải bài tập cuối chương 7 trang 46 SGK Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung trang 34, 35 SGK Toán 7 Kết nối tri thức Tập 2





