SGK Toán 7 – Kết Nối Tri Thức
Giải luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2
Sau khi đã học xong phần lớn các kiến thức của chương 9. Thì bây giờ, hãy cùng HocThatGioi vận dụng các kiến thức đó, hoàn thành tất cả các bài tập ở phần Luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2. Chúng tớ hy vọng, các bạn sẽ dễ dàng hoàn thành các bài tập của mình nhé.
Giải bài 9.14 SGK trang 71
Hãy giải thích: Nếu $M$ là một điểm tùy ý nằm trên cạnh $BC$ hoặc cạnh $CD$ của hình vuông $ABCD$ thì độ dài đoạn thẳng $AM$ luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó. ($H.9.21$)
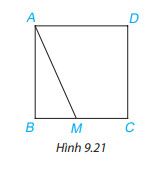
Phương pháp giải:
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ $1$ điểm nằm ngoài $1$ đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ $1$ điểm nằm ngoài $1$ đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Lời giải chi tiết:
Vì $ABCD$ là hình vuông nên $BC = CD$ (tính chất)
* Với $M$ nằm trên cạnh $BC$, ta xét $2$ trường hợp sau:
+) $M$ khác $B$
$AB$ là đường vuông góc kẻ từ $A$ đến $BC; AM$ là đường xiên kẻ từ $A$ đến $BC$ nên $AB < AM$ (đường vuông góc luôn nhỏ hơn đường xiên). Do đó, $AM$ lớn hơn độ dài cạnh của hình vuông
+) $M$ trùng $B$:
$AM = AB$. Do đó, $AM$ bằng độ dài cạnh của hình vuông
Trường hợp $M$ nằm trên cạnh $CD$ tương tự.
Vậy độ dài đoạn thẳng $AM$ luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó.
Vì $ABCD$ là hình vuông nên $BC = CD$ (tính chất)
* Với $M$ nằm trên cạnh $BC$, ta xét $2$ trường hợp sau:
+) $M$ khác $B$
$AB$ là đường vuông góc kẻ từ $A$ đến $BC; AM$ là đường xiên kẻ từ $A$ đến $BC$ nên $AB < AM$ (đường vuông góc luôn nhỏ hơn đường xiên). Do đó, $AM$ lớn hơn độ dài cạnh của hình vuông
+) $M$ trùng $B$:
$AM = AB$. Do đó, $AM$ bằng độ dài cạnh của hình vuông
Trường hợp $M$ nằm trên cạnh $CD$ tương tự.
Vậy độ dài đoạn thẳng $AM$ luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó.
Giải bài 9.15 SGK trang 71
Hỏi có tam giác nào với độ dài ba cạnh là $2,5 cm$; $3,4 cm$ và $6 cm$ không? Vì sao?
Phương pháp giải:
Kiểm tra tổng độ dài $2$ cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không. Nếu thỏa mãn thì có tam giác có ba cạnh như vậy.
Kiểm tra tổng độ dài $2$ cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không. Nếu thỏa mãn thì có tam giác có ba cạnh như vậy.
Lời giải chi tiết:
Ta có: $2,5 + 3,4 = 5,9$ $cm$ $\lt$ $6 cm$ nên không có tam giác nào với độ dài ba cạnh là $2,5 cm$; $3,4 cm$ và $6 cm$.
Ta có: $2,5 + 3,4 = 5,9$ $cm$ $\lt$ $6 cm$ nên không có tam giác nào với độ dài ba cạnh là $2,5 cm$; $3,4 cm$ và $6 cm$.
Giải bài 9.16 SGK trang 71
Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là$ 2 cm$ và $5 cm$.
Phương pháp giải:
+ Xét $2$ trường hợp: cạnh còn lại dài $2 cm$ hoặc $5 cm$
+ Từ bất đẳng thức tam giác, suy ra độ dài cạnh còn lại.
+ Chu vi tam giác = Tổng độ dài $3$ cạnh
+ Xét $2$ trường hợp: cạnh còn lại dài $2 cm$ hoặc $5 cm$
+ Từ bất đẳng thức tam giác, suy ra độ dài cạnh còn lại.
+ Chu vi tam giác = Tổng độ dài $3$ cạnh
Lời giải chi tiết:
Vì tam giác đã cho cân nên cạnh còn lại có độ dài là $2 cm$ hoặc $5 cm$.
+) Nếu độ dài cạnh còn lại là $2 cm$:
Ta có: $2 + 2 \lt 5$ ( không thỏa mãn bất đẳng thức tam giác) (Loại).
+) Nếu độ dài cạnh còn lại là $5 cm$:
$2 + 5 \gt 5$ (thỏa mãn bất đẳng thức tam giác)
Do đó, độ dài cạnh còn lại của tam giác là $5 cm$.
Chu vi tam giác đó là:
$2 + 5 + 5 = 12$ $(cm)$
Vì tam giác đã cho cân nên cạnh còn lại có độ dài là $2 cm$ hoặc $5 cm$.
+) Nếu độ dài cạnh còn lại là $2 cm$:
Ta có: $2 + 2 \lt 5$ ( không thỏa mãn bất đẳng thức tam giác) (Loại).
+) Nếu độ dài cạnh còn lại là $5 cm$:
$2 + 5 \gt 5$ (thỏa mãn bất đẳng thức tam giác)
Do đó, độ dài cạnh còn lại của tam giác là $5 cm$.
Chu vi tam giác đó là:
$2 + 5 + 5 = 12$ $(cm)$
Giải bài 9.17 SGK trang 71
Độ dài hai cạnh của một tam giác bằng $7 cm$ và $2 cm$. Tính độ dài cạnh còn lại biết rằng số đo của nó theo $xentimet$ là một số tự nhiên lẻ.
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài $2$ cạnh còn lại: $b – c \lt a \lt b + c$ (với $a, b, c$ là độ dài $3$ cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh cần tìm là số tự nhiên lẻ.
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài $2$ cạnh còn lại: $b – c \lt a \lt b + c$ (với $a, b, c$ là độ dài $3$ cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh cần tìm là số tự nhiên lẻ.
Lời giải chi tiết:
Gọi độ dài cạnh cần tìm là $x$ ($cm$) ( $x$ là số tự nhiên lẻ)
Áp dụng bất đẳng thức tam giác vào tam giác đã cho, ta có:
$7 – 2 \lt x \lt 7 + 2$
$5 \lt x \lt 9$
Mà $x$ là số tự nhiên lẻ
$ \Longrightarrow x = 7$
Vậy độ dài cạnh còn lại của tam giác đó là $7 cm$.
Gọi độ dài cạnh cần tìm là $x$ ($cm$) ( $x$ là số tự nhiên lẻ)
Áp dụng bất đẳng thức tam giác vào tam giác đã cho, ta có:
$7 – 2 \lt x \lt 7 + 2$
$5 \lt x \lt 9$
Mà $x$ là số tự nhiên lẻ
$ \Longrightarrow x = 7$
Vậy độ dài cạnh còn lại của tam giác đó là $7 cm$.
Giải bài 9.18 SGK trang 71
Biết rằng hai cạnh của tam giác có độ dài $a$ và $b$. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn $2a$ và nhỏ hơn $2(a+b)$.
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài $2$ cạnh còn lại: $b – c < a < b + c$ ( với $a, b, c$ là độ dài $3$ cạnh của tam giác)
Chu vi tam giác = Tổng độ dài $3$ cạnh
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài $2$ cạnh còn lại: $b – c < a < b + c$ ( với $a, b, c$ là độ dài $3$ cạnh của tam giác)
Chu vi tam giác = Tổng độ dài $3$ cạnh
Lời giải chi tiết:
Gọi độ dài cạnh còn lại của tam giác là $c$.
Áp dụng bất đẳng thức tam giác, ta có:
$a – b < c < a + b$
$ \Longleftrightarrow a – b + a + b < c + a + b < a + b + a + b$
$\Longleftrightarrow 2a <$ chu vi tam giác $< 2 (a+b)$
Vậy chu vi của tam giác đó lớn hơn $2a$ và nhỏ hơn $2(a+b)$.
Gọi độ dài cạnh còn lại của tam giác là $c$.
Áp dụng bất đẳng thức tam giác, ta có:
$a – b < c < a + b$
$ \Longleftrightarrow a – b + a + b < c + a + b < a + b + a + b$
$\Longleftrightarrow 2a <$ chu vi tam giác $< 2 (a+b)$
Vậy chu vi của tam giác đó lớn hơn $2a$ và nhỏ hơn $2(a+b)$.
Giải bài 9.19 SGK trang 71
Hai khu vườn $A$ và $B$ nằm về một phía của con kênh $d$. Hãy xác định bên bờ kênh cùng phía với $A$ và $B$, một điểm $C$ để đặt máy bơm nước từ kênh tưới cho hai khu vườn sao cho tổng độ dài đường ống dẫn nước từ máy bơm đế hai khu vườn là ngắn nhất.
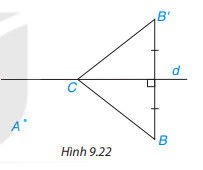
Phương pháp giải:
Gọi $B’$ là điểm sao cho $d$ là đường trung trực của $BB’$.
Áp dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Gọi $B’$ là điểm sao cho $d$ là đường trung trực của $BB’$.
Áp dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Lời giải chi tiết:
Gọi $B’$ là điểm sao cho $d$ là đường trung trực của $BB’$
Khi đó, $CB = CB’$ (tính chất đường trung trực của đoạn thẳng)
+) Nếu $A,C,B’$ không thẳng hàng thì ta lập được tam giác $AB’C$. Khi đó, theo bất đẳng thức tam giác, ta có:
$AC + CB’ > AB’$ hay $AC + CB > AB’$, tức là độ dài đường ống dẫn nước lớn hơn độ dài $AB’$.
+) Nếu $A,C,B’$ thẳng hàng thì $C$ nằm giữa $A$ và $B’$ nên $AC + CB’ = AB’$, tức là độ dài đường ống dẫn nước bằng độ dài $AB’$.
Vậy khi đặt điểm $C$ nằm trên bờ kênh $d$, sao cho $A,C,B’$ thẳng hàng thì tổng độ dài đường ống dẫn nước từ máy bơm đế hai khu vườn là ngắn nhất .
Gọi $B’$ là điểm sao cho $d$ là đường trung trực của $BB’$
Khi đó, $CB = CB’$ (tính chất đường trung trực của đoạn thẳng)
+) Nếu $A,C,B’$ không thẳng hàng thì ta lập được tam giác $AB’C$. Khi đó, theo bất đẳng thức tam giác, ta có:
$AC + CB’ > AB’$ hay $AC + CB > AB’$, tức là độ dài đường ống dẫn nước lớn hơn độ dài $AB’$.
+) Nếu $A,C,B’$ thẳng hàng thì $C$ nằm giữa $A$ và $B’$ nên $AC + CB’ = AB’$, tức là độ dài đường ống dẫn nước bằng độ dài $AB’$.
Vậy khi đặt điểm $C$ nằm trên bờ kênh $d$, sao cho $A,C,B’$ thẳng hàng thì tổng độ dài đường ống dẫn nước từ máy bơm đế hai khu vườn là ngắn nhất .
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải Luyện tập chung SGK chương 9 trang 70, 71 Toán 7 Kết nối tri thức Tập 2. Hi vọng các bạn có hoàn thành tốt tất cả các bài tập của mình và có một buổi học thật thú vị nhé. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương tam giác
- Giải SGK Bài tập cuối chương 7 trang 119, 120 Toán 7 Cánh diều tập 2
- Giải SGK Bài tập cuối chương 8 trang 84 Toán 7 Chân trời sáng tạo tập 2
- Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 9 trang 84 Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung trang 82, 83 SGK Toán 7 Kết nối tri thức Tập 2
- Giải SGK Luyện tập chung trang 86 Toán 7 Kết nối tri thức tập 1





