SGK Toán 7 – Kết Nối Tri Thức
Giải Luyện tập chung trang 82, 83 SGK Toán 7 Kết nối tri thức Tập 2
Hôm nay, HocThatGioi sẽ đồng hành cùng bạn củng cố lại những kiến thức đã học ở chương 9. Bằng cách áp dụng những công thức, lý thuyết đã học. Để giải tất cả các bài tập ở phần Luyện tập chung Trang 82, 83 SGK Toán 7 Kết nối tri thức tập 2. Hy vọng, sau bài viết này các bạn có thể nắm rõ những kiến thức đã học và có thể áp dụng chúng một cách dễ dàng theo những lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải bài 9.31 trang 83
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Phương pháp giải:
– Chứng minh: $\Delta ABM$ = $\Delta ACM$ (2 cạnh góc vuông)
– Chứng minh: $\Delta ABM$ = $\Delta ACM$ (2 cạnh góc vuông)
Lời giải chi tiết:
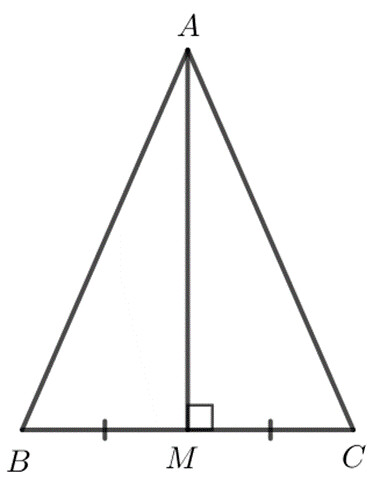
Giả sử tam giác $ABC$ có $AM$ vừa là đường trung tuyến, vừa là đường cao xuất phát từ đỉnh $A$.
Do $AM$ là đường trung tuyến của tam giác $ABC$ nên $M$ là trung điểm của $BC$.
Do đó $BM = CM$.
Xét $\Delta ABM$ vuông tại $M$ và $\Delta ACM$ vuông tại $M$ có:
$AM$ chung.
$BM = CM$ (chứng minh trên).
Suy ra $\Delta ABM = \Delta ACM$ (2 cạnh góc vuông).
Do đó $AB = AC$ (2 cạnh tương ứng).
Tam giác $ABC$ có $AB = AC$ nên tam giác $ABC$ cân tại $A$.
Do $AM$ là đường trung tuyến của tam giác $ABC$ nên $M$ là trung điểm của $BC$.
Do đó $BM = CM$.
Xét $\Delta ABM$ vuông tại $M$ và $\Delta ACM$ vuông tại $M$ có:
$AM$ chung.
$BM = CM$ (chứng minh trên).
Suy ra $\Delta ABM = \Delta ACM$ (2 cạnh góc vuông).
Do đó $AB = AC$ (2 cạnh tương ứng).
Tam giác $ABC$ có $AB = AC$ nên tam giác $ABC$ cân tại $A$.

Giải bài 9.32 trang 83
Cho ba điểm phân biệt thẳng hàng $A, B, C$. Gọi $d$ là đường thẳng vuông góc với $AB$ tại $A$. Với điểm $M$ thuộc $d, M$ khác $A$, vẽ đường thẳng $CM$. Qua $B$ kẻ đường thẳng vuông góc với đường thẳng $CM$, cắt $d$ tại $N$. Chứng minh đường thẳng $BM$ vuông góc với đường thẳng $CN$.
Phương pháp giải:
– Ba đường cao trong tam giác đồng quy tại một điểm.
– Ba đường cao trong tam giác đồng quy tại một điểm.
Lời giải chi tiết:
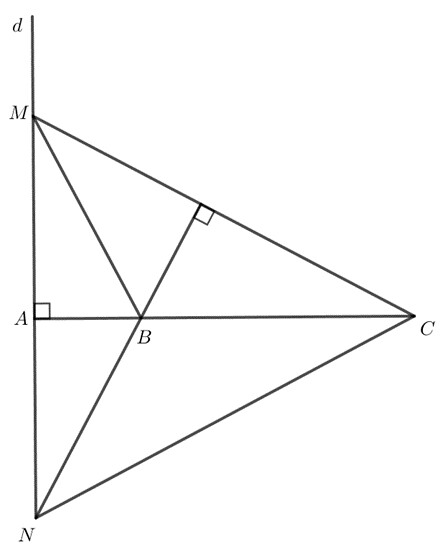
Xét tam giác $MNC$ có $2$ đường cao $CA$ và $NB$ cắt nhau tại $B$
$\Rightarrow B$ là trực tâm của tam giác $MNC$
$\Rightarrow MB \perp CM$
$\Rightarrow B$ là trực tâm của tam giác $MNC$
$\Rightarrow MB \perp CM$

Giải bài 9.33 trang 83
Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?
Phương pháp giải:
– Lấy ba điểm phân biệt $A, B, C$ trên đường viền ngoài mảnh tôn.
– Xác định giao của các đường trung trực.
– Lấy ba điểm phân biệt $A, B, C$ trên đường viền ngoài mảnh tôn.
– Xác định giao của các đường trung trực.
Lời giải chi tiết:
Ta thực hiện theo các bước sau:
Bước $1$. Xác định ba điểm $A, B, C$.
Bước $2$. Xác định ba đường trung trực của tam giác $ABC$.
Bước $3$. Xác định giao điểm của ba đường trung trực của tam giác $ABC$.
Điểm đó là tâm của mảnh tôn
Ta thực hiện theo các bước sau:
Bước $1$. Xác định ba điểm $A, B, C$.
Bước $2$. Xác định ba đường trung trực của tam giác $ABC$.
Bước $3$. Xác định giao điểm của ba đường trung trực của tam giác $ABC$.
Điểm đó là tâm của mảnh tôn
Giải bài 9.34 trang 83
Cho tam giác $ABC$. Kẻ tia phân giác $At$ của góc tạo bởi tia $AB$ và tia đối của $AC$. Chứng minh rằng nếu đường thẳng chứa tia $At$ song song với đường thẳng $BC$ thì tam giác $ABC$ cân tại $A$.
Phương pháp giải:
$At \parallel BC$
$\widehat{ABC} = \widehat{BAt}$ (Hai góc sole trong)
$\widehat{ACB} = \widehat{MAt}$ (Hai góc đồng vị)
$At \parallel BC$
$\widehat{ABC} = \widehat{BAt}$ (Hai góc sole trong)
$\widehat{ACB} = \widehat{MAt}$ (Hai góc đồng vị)
Lời giải chi tiết:
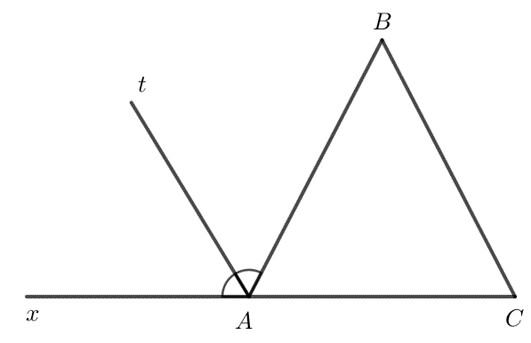
Gọi $AM$ là tia đối của $AC$. $At$ là đường phân giác của $\widehat{MAB}$ $\Rightarrow \widehat{MAt} =\widehat{BAt}$
Ta có: $At\parallel BC$ nên:
$\widehat{ABC}=\widehat{BAt}$ (Hai góc so le trong)
$\widehat{ACB} = \widehat{MAt}$ (Hai góc đồng vị)
Mà $\widehat{MAt}= \widehat{BAt}$ $\Rightarrow \widehat{ABC}= \widehat{ACB}$ Vậy tam giác $ABC$ cân tại $A$ (Dấu hiệu nhận biết tam giác cân)
Ta có: $At\parallel BC$ nên:
$\widehat{ABC}=\widehat{BAt}$ (Hai góc so le trong)
$\widehat{ACB} = \widehat{MAt}$ (Hai góc đồng vị)
Mà $\widehat{MAt}= \widehat{BAt}$ $\Rightarrow \widehat{ABC}= \widehat{ACB}$ Vậy tam giác $ABC$ cân tại $A$ (Dấu hiệu nhận biết tam giác cân)

Giải bài 9.35 trang 83
Kí hiệu $S_{ABC}$ là diện tích tam giác $ABC$. Gọi $G$ là trọng tâm tam giác $ABC$, $M$ là trung điểm $BC$.
a) Chứng minh $S_{GBC}=\frac{1}{3}S_{ABC}$
$Gợi$ $ý$: Sử dụng $GM=\frac{1}{3}AM$ để chứng minh $S_{GMB}=\frac{1}{3}S_{ABM}$, $S_{GCM} = \frac{1}{3}S_{ACM}$.
b) Chứng minh $S_{GCA}=S_{GAB}=\frac{1}{3}S_{ABC}$.
a) Chứng minh $S_{GBC}=\frac{1}{3}S_{ABC}$
$Gợi$ $ý$: Sử dụng $GM=\frac{1}{3}AM$ để chứng minh $S_{GMB}=\frac{1}{3}S_{ABM}$, $S_{GCM} = \frac{1}{3}S_{ACM}$.
b) Chứng minh $S_{GCA}=S_{GAB}=\frac{1}{3}S_{ABC}$.
Phương pháp giải:
a) Kẻ $BP\perp AM$, $CN \perp AM$
Sử dụng $GM=\frac{1}{3}AM$ để chứng minh $S_{GMB}=\frac{1}{3}S_{ABM},S_{GCM}=\frac{1}{3}S_{ACM}$.
b) – Chứng minh $S_{GAB}=S_{GAC}$.
– Sử dụng $S_{ABC}=S_{GAB}+S_{GAC}+S_{GBC}$.
a) Kẻ $BP\perp AM$, $CN \perp AM$
Sử dụng $GM=\frac{1}{3}AM$ để chứng minh $S_{GMB}=\frac{1}{3}S_{ABM},S_{GCM}=\frac{1}{3}S_{ACM}$.
b) – Chứng minh $S_{GAB}=S_{GAC}$.
– Sử dụng $S_{ABC}=S_{GAB}+S_{GAC}+S_{GBC}$.
Lời giải chi tiết:
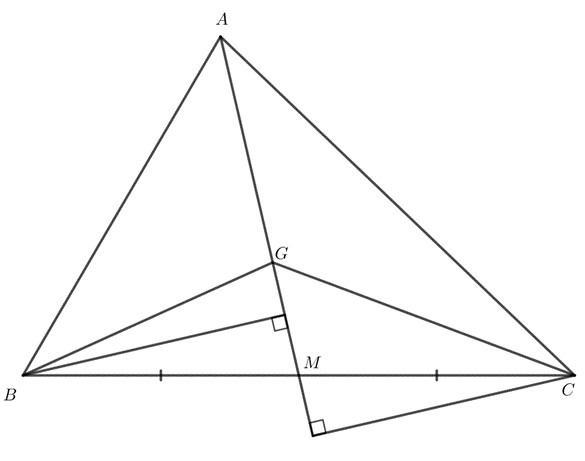
a) Do $G$ là trọng tâm của tam giác $ABC$ và $M$ là trung điểm của $BC$ nên $GM = \frac{1}{3}AM$.
$\Delta ABM$ và $\Delta MBG$ có chung đường cao kẻ từ $B$ đến $AM$ nên tỉ số diện tích giữa $\Delta MBG$ và $\Delta ABM$ bằng tỉ số của hai đáy $GM$ và $AM$.
Ta có $GM = \frac{1}{3}AM$ nên $S_{MBG} = \frac{1}{3}S_{ABM}$.
$\Delta ABM$ và $\Delta MBG$ có chung đường cao kẻ từ $C$ đến $AM$ nên tỉ số diện tích giữa $\Delta MBG$ và $\Delta ABM$ bằng tỉ số của hai đáy $GM$ và $AM$.
Ta có $GM = \frac{1}{3}AM$ nên $S_{MCG} = \frac{1}{3}S_{ACM}$.
Do đó $S_{MBG} + S_{MCG} = \frac{1}{3}S_{ABM} + \frac{1}{3}S_{ACM}$ hay $S_{GBC} = \frac{1}{3}S_{ABC}$.
b) Ta có $AG = 2GM$ nên $S_{GCA} = 2S_{MCG}$; $S_{GAB} = 2S_{MBG}$.
Do $BC = 2MB = 2MC$ nên $S_{GBC} = 2S_{MCG} = 2S_{MBG}$.
Do đó $S_{GCA} = S_{GAB} = S_{GBC} = \frac{1}{3}S_{ABC}$.
$\Delta ABM$ và $\Delta MBG$ có chung đường cao kẻ từ $B$ đến $AM$ nên tỉ số diện tích giữa $\Delta MBG$ và $\Delta ABM$ bằng tỉ số của hai đáy $GM$ và $AM$.
Ta có $GM = \frac{1}{3}AM$ nên $S_{MBG} = \frac{1}{3}S_{ABM}$.
$\Delta ABM$ và $\Delta MBG$ có chung đường cao kẻ từ $C$ đến $AM$ nên tỉ số diện tích giữa $\Delta MBG$ và $\Delta ABM$ bằng tỉ số của hai đáy $GM$ và $AM$.
Ta có $GM = \frac{1}{3}AM$ nên $S_{MCG} = \frac{1}{3}S_{ACM}$.
Do đó $S_{MBG} + S_{MCG} = \frac{1}{3}S_{ABM} + \frac{1}{3}S_{ACM}$ hay $S_{GBC} = \frac{1}{3}S_{ABC}$.
b) Ta có $AG = 2GM$ nên $S_{GCA} = 2S_{MCG}$; $S_{GAB} = 2S_{MBG}$.
Do $BC = 2MB = 2MC$ nên $S_{GBC} = 2S_{MCG} = 2S_{MBG}$.
Do đó $S_{GCA} = S_{GAB} = S_{GBC} = \frac{1}{3}S_{ABC}$.

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải Luyện tập chung trang 82, 83 Toán 7 Kết nối tri thức Tập 2. Hi vọng các bạn có hoàn thành tốt tất cả các bài tập của mình và có một buổi học thật thú vị nhé. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương tam giác
- Giải SGK Bài tập cuối chương 7 trang 119, 120 Toán 7 Cánh diều tập 2
- Giải SGK Bài tập cuối chương 8 trang 84 Toán 7 Chân trời sáng tạo tập 2
- Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 9 trang 84 Toán 7 Kết nối tri thức Tập 2
- Giải SGK Luyện tập chung trang 86 Toán 7 Kết nối tri thức tập 1
- Giải luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2





