Giải SGK Bài 1 Chương 7 trang 6, 7, 8, 9, 10 Toán 10 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các hoạt động khởi động, vận dụng, bài tập trong bài Dấu của tam thức bậc hai . Các bài tập sau đây thuộc Bài 1 Chương VII SGK Toán 10 Chân trời sáng tạo tập 2 ở các trang 6, 7, 8, 9, 10. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài 1 chương 7 Toán 10 Chân trời sáng tạo tập 2
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động khởi động, khám phá, thực hành và vận dụng ở các trang 6, 7, 8, 9 trong sách Toán 10 Chân trời sáng tạo một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
Hoạt động khám phá 1 trang 6
a) Biểu thức $f(x)$ là đa thức bậc mấy?
b) Xác định dấu của $f(2)$.
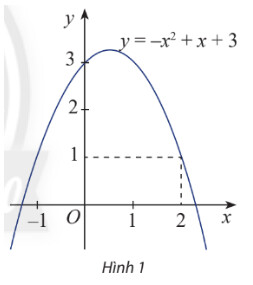
a) Xác định số mũ cao nhất
b) Thay $x=2$ vào $f(x)$, so sánh với 0
a) Số mũ cao nhất của hàm số là 2 , suy ra biểu thức $f(x)$ đã cho là đa thức bậc hai
b) Thay $x=2$ vào $f(x)$ ta có:
$f(2)=-2^2+2+3=1>0$
Suy ra $f(2)$ dương.
Hoạt đông khám phá 2 trang 8
– Các nghiệm (nếu có) và dấu của biệt thức $\Delta$.
– Các khoảng giá trị của $x$ mà trên đó $f(x)$ cùng dấu với hệ số của $x^{2}$.
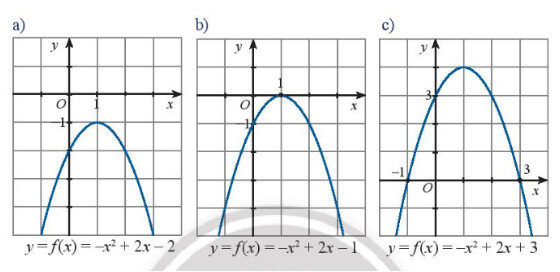
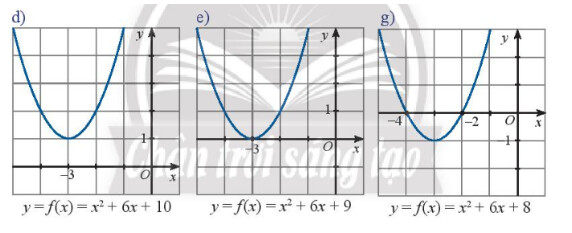
Bước 1: Xác định nghiệm của hàm số là giao của đồ thị và trục hoành
Bước 2: Xác định biệt thức $\Delta=b^2-4 a c$ và xác định dấu của nó
Bước 3: Dựa vào đồ thị xác định dấu của $f(x)$
+) Phần đồ thị nằm trên trục hoành là $f(x)>0$
+) Phần đồ thị nằm dưới trục hoành là $f(x)<0$
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức $\Delta=2^2-4 .(-1) .(-2)=-4<0$
Ta thấy hệ số của $x^2$ là $-1<0$
Đồ thị nằm dưới trục hoành với mọi $x$
Nên $f(x)$ cùng dấu với hệ số của $x^2$ với $\forall x \in \mathbb{R}$
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép $x_1=x_2=1$
Biệt thức $\Delta=2^2-4 .(-1) .(-1)=0$
Ta thấy hệ số của $x^2$ là $-10$
Ta thấy hệ số của $x^2$ là $-1<0$
Đồ thị nằm dưới trục hoành khi $x \in(-\infty,-1) \cup(3,+\infty)$
Đồ thị nằm trên trục hoành với mọi $x \in(-1,3)$
Nên $f(x)$ cùng dấu với hệ số của $x^2$ khi $x \in(-\infty,-1) \cup(3,+\infty)$
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức $\Delta=6^2-4.1 .10=-40$
Đồ thị nằm trên trục hoành với mọi $x$
Nên $f(x)$ cùng dấu với hệ số của $x^2$ với mọi $x \in \mathbb{R}$
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép $x_1=x_2=-3$
Biệt thức $\Delta=6^2-4.1 .9=0$
Ta thấy hệ số của $x^2$ là $1>0$
Đồ thị nằm trên trục hoành với mọi $x$
Nên $f(x)$ cùng dấu với hệ số của $x^2$ với mọi $x \in \mathbb{R}$
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt $x_1=-4 ; x_2=-2$
Biệt thức $\Delta=6^2-4.1 .8=4>0$
Ta thấy hệ số của $x^2$ là $1>0$
Đồ thị nằm trên trục hoành khi $x \in(-\infty,-4) \cup(-2,+\infty)$
Đồ thị nằm dưới trục hoành với mọi $x \in(-4,-2)$
Nên $f(x)$ cùng dấu với hệ số của $x^2$ khi $x \in(-\infty,-4) \cup(-2,+\infty)$
Thực hành 1 trang 7
a) $f(x)=2 x^2+x-1$;
b) $g(x)=-x^4+2 x^2+1$
c) $h(x)=-x^2+\sqrt{2} . x-3$
a) Biểu thức $f(x)=2 x^2+x-1$ là một tam thức bậc hai
$f(1)=2.1^2+1-1=2>0 \text { nên } f(x) \text { dương tại } x=1$
b) Biểu thức $g(x)=-x^4+2 x^2+1$ không phải là một tam thức bậc hai
c) Biểu thức $h(x)=-x^2+\sqrt{2} . x-3$ là một tam thức bậc hai
$h(1)=-1^2+\sqrt{2} .1-3=\sqrt{2}-4<0 \text { nên } h(x) \text { âm tại } x=1$
Thực hành 2 trang 7
а) $f(x)=2 x^2-5 x+2$
b) $g(x)=-x^2+6 x-9$
c) $h(x)=4 x^2-4 x+9$
Bước 1: Xác định biệt thức $\Delta=b^2-4 a c$
Bước 2: Xét dấu của $\Delta$
Bước 3: Tìm nghiệm
+) Nếu $\Delta>0 \Rightarrow x_1=\frac{-b+\sqrt{\Delta}}{2 a} ; x_2=\frac{-b-\sqrt{\Delta}}{2 a}$
+) Nếu $\Delta=0 \Rightarrow x_1=x_2=\frac{-b}{2 a}$
+) Nếu $\Delta=0$ thì tam thức bậc hai vô nghiệm
a) Tam thức bậc hai $f(x)=2 x^2-5 x+2$ có $\Delta=(-5)^2-4.2 .2=9$
$\Delta>0$, do đó $f(x)$ có hai nghiệm phân biệt là
$x_1=\frac{5+\sqrt{9}}{4}=2 \text { và } x_1=\frac{5-\sqrt{9}}{4}=\frac{1}{2}$
b) Tam thức bậc hai $g(x)=-x^2+6 x-9$ có $\Delta=6^2-4$. (-1) $\cdot(-9)=0$
$\Delta=0$, do đó $g(x)$ có nghiệm kép $x_1=x_2=\frac{-6}{2 .(-1)}=3$
c) Tam thức bậc hai $h(x)=4 x^2-4 x+9$ có $\Delta=(-4)^2-4.4 .9=-128$
$\Delta<0$, do đó $h(x)$ vô nghiệm
Thực hành 3 trang 9
a) $f(x)=2 x^2-3 x-2$
b) $g(x)=-x^2+2 x-3$
Bước 1: Tính và xác định dấu của biệt thức $\Delta=b^2-4 a c$
Bước 2: Xác định nghiệm của $f(x)$ (nếu có) $x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
Bước 3: Xác định dấu của hệ số $a$
Bước 4: Xác định dấu của $f(x)$
a) $f(x)=2 x^2-3 x-2$ có $\Delta=25>0$, hai nghiệm phân biệt là $x_1=-\frac{1}{2} ; x_2=2$ và $a=2>0$
Ta có bảng xét dấu như sau:
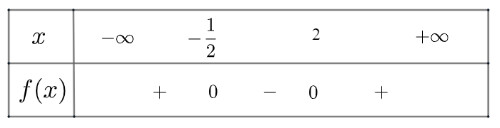
Vậy $f(x)$ âm trong khoảng $\left(-\frac{1}{2}, 2\right)$ và dương trong hai khoảng $\left(-\infty,-\frac{1}{2}\right)$ và $(2,+\infty)$
b) $g(x)=-x^2+2 x-3$ có $\Delta=2^2-4.(-1) .(-3)=-8<0$ và $a=-1<0$
Vậy $g(x)$ âm với mọi $x \in \mathbb{R}$
Vận dụng trang 9
Bước 1: Tính và xác định dấu của biệt thức $\Delta=b^2-4 a c$
Bước 2: Xác định nghiệm của $h(x)$ (nếu có) $x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
Bước 3: Xác định dấu của hệ số $a$
Bước 4: Xác định dấu của $h(x)$
$h(x)=-0,006 x^2+1,2 x-30$ có $\Delta=1,2^2-4 \cdot(-0,006) \cdot(-30)=\frac{18}{25}>0$, hai nghiệm phân biệt là $x_1=100-50 \sqrt{2} ; x_2=100+50 \sqrt{2}$ và $a=-0,006<0$
Ta có bảng xét dấu $h(x)$ như sau:
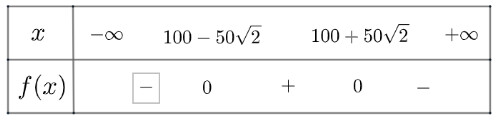
Vậy vòm cầu cao hơn mặt cầu là khoảng cách từ $100-50 \sqrt{2}(\mathrm{~m})$ đến $100+50 \sqrt{2}(\mathrm{~m})$ (cách từ $O$ ), vòm vòm cầu thấp hơn mặt cầu là khoảng cách từ $O$ đến $100-50 \sqrt{2}(\mathrm{~m})$ và từ $100+50 \sqrt{2}(\mathrm{~m})$ đến $200(\mathrm{~m})$ (cách từ $O$ )
Giải bài tập SGK bài Dấu của tam thức bậc hai Toán 10 Chân trời sáng tạo tập 2
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Dấu của tam thức bậc hai trang 10 sách Toán 10 Chân trời sáng tạo dưới đây nhé!
Bài tập 1 trang 9
a) $4 x^2+3 x+1$
b) $x^3+3 x^2-1$
c) $2 x^2+4 x-1$
Tam thức bậc hai là đa thức có bậc cao nhất của biến là 2
a) Đa thức $4 x^2+3 x+1$ là tam thức bậc hai
b) Đa thức $x^3+3 x^2-1$ không là tam thức bậc hai
c) Đa thức $2 x^2+4 x-1$ là tam thức bậc hai
Bài tập 2 trang 9
a) $(m+1) x^2+2 x+m$
b) $m x^3+2 x^2-x+m$
c) $-5 x^2+2 x-m+1$
Bước 1: Xác định $a$ là hệ số của $x^2$
Bước 2: Đa thức $a x^2+b x+c$ được gọi là tam thức bậc hai khi $a \neq 0$
a) Ta có: $a=m+1$
Để đa thức $(m+1) x^2+2 x+m$ là tam thức bậc hai khi và chỉ khi $m+1 \neq 0$
$\Leftrightarrow m \neq-1$
Vậy khi $m \neq-1$ thì đa thức $(m+1) x^2+2 x+m$ là tam thức bậc hai
b) Ta có: $a=2$
Để đa thức $m x^3+2 x^2-x+m$ là tam thức bậc hai khi và chỉ khi $m=0$
Vậy khi $m=0$ thì đa thức $m x^3+2 x^2-x+m$ là tam thức bậc hai
c) Ta có $a=-5$
Hệ số ckhông ảnh hưởng đến tam thức bậc hai
Vậy đa thức $-5 x^2+2 x-m+1$ là tam thức bậc hai với mọi $m$
Bài tập 3 trang 10
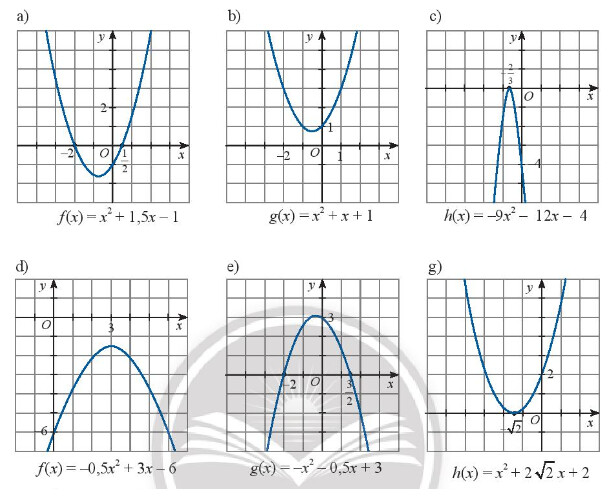
Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)
Bước 2: Xác định khoảng mà $f(x)>0$ (khoảng đồ thị nằm trên trục hoành)
Bước 3: Xác định khoảng mà $f(x)<0$ (khoảng đồ thị nằm dưới trục hoành)
Bước 4: Lập bảng xét dấu
a) Tam thức $f(x)=x^2+1,5 x-1$ có hai nghiệm phân biệt $x_1=-2 ; x_2=\frac{1}{2}$ $f(x)>0$ khi $x \in(-\infty,-2) \cup\left(\frac{1}{2},+\infty\right)$ và $f(x)<0$ khi $x \in\left(-2, \frac{1}{2}\right)$
Ta có bảng xét dấu như sau:
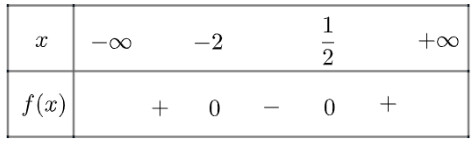
b) Tam thức $g(x)=x^2+x+1$ vô nghiệm, $g(x)>0 \forall x \in \mathbb{R}$
Ta có bảng xét dấu như sau:
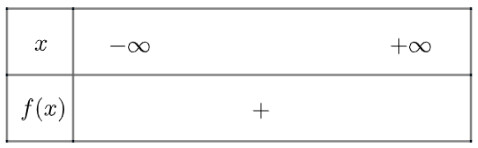
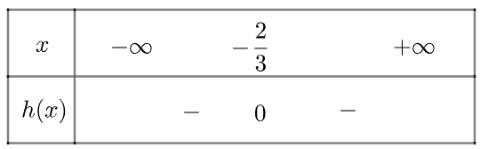
c) Tam thức $h(x)=-9 x^2-12 x-4$ có nghiệm kép $x_1=x_2=-\frac{2}{3}$ và $h(x)<0 \forall x \neq-\frac{2}{3}$
Ta có bảng xét dấu như sau:
d) Tam thức $f(x)=-0,5 x^2+3 x-6$ vô nghiệm và $f(x)<0 \forall x \in \mathbb{R}$
Ta có bảng xét dấu như sau:

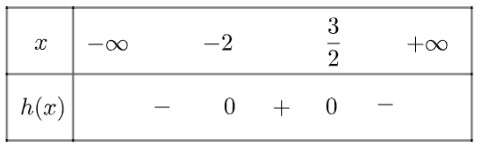
e) Tam thức $g(x)=-x^2-0,5 x+3$ có hai nghiệm $x_1=-2, x_2=\frac{3}{2}$
$g(x)>0$ khi $x \in\left(-2, \frac{3}{2}\right)$ và $g(x)<0$ khi $x \in(-\infty,-2) \cup\left(\frac{3}{2},+\infty\right)$
Ta có bảng xét dấu như sau:
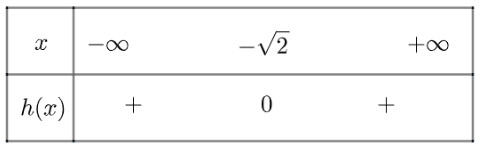
g) Tam thức $h(x)=x^2+2 \sqrt{2} x+2$ có nghiệm kép $x_1=x_2=-\sqrt{2}$
$h(x)>0 \forall x \neq-\sqrt{2}$
Ta có bảng xét dấu như sau:
Bài tập 4 trang 10
a) $f(x)=2 x^2+4 x+2$
b) $f(x)=-3 x^2+2 x+21$
c) $f(x)=-2 x^2+x-2$
d) $f(x)=-4 x(x+3)-9$
e) $f(x)=(2 x+5)(x-3)$
Bước 1: Tính và xác định dấu của biệt thức $\Delta=b^2-4 a c$
Bước 2: Xác định nghiệm của $f(x)$ (nếu có) $x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
Bước 3: Xác định dấu của hệ số $a$
Bước 4: Xác định dấu của $f(x)$
a) $f(x)=2 x^2+4 x+2$ có $\Delta=0$, có nghiệm kép là $x_1=x_2=-1$
và $a=2>0$
Ta có bảng xét dấu như sau:
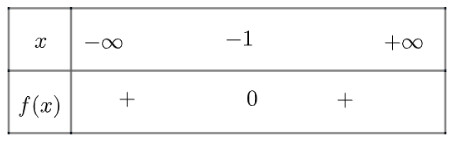
Vậy $f(x)$ dương với mọi $x \neq-1$
b) $f(x)=-3 x^2+2 x+21$ có $\Delta=256>0$, hai nghiệm phân biệt là $x_1=-\frac{7}{3} ; x_2=3$
và $a=-3<0$
Ta có bảng xét dấu như sau:
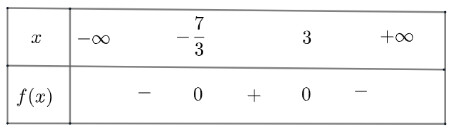
Vậy $f(x)$ dương với $x \in\left(-\frac{7}{3} ; 3\right)$ và âm khi $x \in\left(-\infty ;-\frac{7}{3}\right) \cup(3 ;+\infty)$
c) $f(x)=-2 x^2+x-2$ có $\Delta=-15<0$, tam thức vô nghiệm
và $a=-2<0$
Ta có bảng xét dấu như sau:

Vậy $f(x)$ âm với mọi $x \in \mathbb{R}$
d) $f(x)=-4 x(x+3)-9=-4 x^2-12 x-9$ có $\Delta=0$, tam thức có nghiệm kép $x_1=x_2=-\frac{3}{2}$ và $a=-4<0$
Ta có bảng xét dấu như sau:
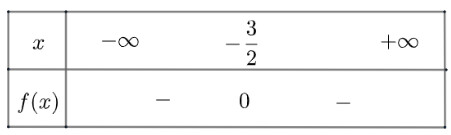
Vậy $f(x)$ âm với mọi $x \neq-\frac{3}{2}$
e) $f(x)=(2 x+5)(x-3)=2 x^2-x-15$ có $\Delta=121>0$, có hai nghiệm phân biệt $x_1=-\frac{5}{2} ; x_2=3$ và có $a=2>0$
Ta có bảng xét dấu như sau:
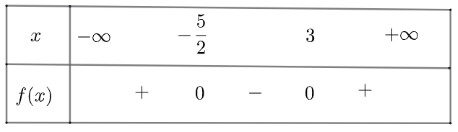
Vậy $f(x)$ âm với $x \in\left(-\frac{5}{2} ; 3\right)$ và dương khi $x \in\left(-\infty ;-\frac{5}{2}\right) \cup(3 ;+\infty)$
Bài tập 5 trang 10
Phương pháp giải – Xem chi tiết
Bước 1: Tính và xác định dấu của biệt thức $\Delta=b^2-4 a c$
Bước 2: Xác định nghiệm của $h(x)$ (nếu có) $x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
Bước 3: Lập bảng xét dấu
Bước 4: Dựa vào bảng xét dấu đưa ra các khoảng theo yêu cầu
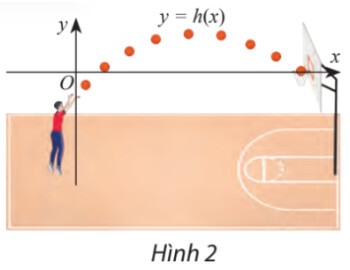
+) Khoảng mà $h(x)>0$ là khoảng bóng nằm cao hơn vành rổ
+) Khoảng mà $h(x)<0$ là khoảng bóng nằm thấp hơn vành rổ
+) Khoảng mà $h(x)=0$ là khoảng bóng nằm ngang vành rổ
$h(x)=-0,1 x^2+x-1$ có $\Delta=\frac{3}{5}>0$, có hai nghiệm phân biệt là $x_1=5-\sqrt{15} ; x_2=5+\sqrt{15}$
Ta có bảng xét dấu như sau:

Vậy khoảng bóng nằm trên vành rổ là $x \in(1,2 ; 8,9)$ mét
khoảng bóng nằm dưới vành rổ là $x \in(-\infty ; 1,2) \cup(8,9 ;+\infty)$ mét
khoảng bóng nằm ngang vành rổ là $x \simeq\{1,2 ; 8,9\}$
Bài tập 6 trang 10
Bước 1: Lập hiệu giữa diện tích mới và diện tích cũ $f(x)=20.15-(20+x)(15-x)$ với $x>0$
Bước 2: Tìm các khoảng thỏa mãn yêu cầu
+) Khoảng mà $f(x)>0$ là khoảng diện tích tăng lên
+) Khoảng mà $f(x)<0$ là khoảng diện tích giảm đi
+) Khoảng mà $f(x)=0$ là khoảng diện tích không đổi
Theo giải thiết ta có tam thức sau: $f(x)=20.15-(20+x)(15-x)=x^2+5 x$
Tam thức có $\Delta=25>0$, có hai nghiệm phân biệt $x_1=0 ; x_2=-5$
Vậy khoảng diện tích tăng lên là $x>0$ và $x<-5$, khoảng diện giảm đi là $x \in(-5 ; 0)$ và diện tích không đổi khi $x=0$ và $x=-5$
Bài tập 7 trang 10
Bước 1: Chuyển bất phương trình tương đương với $f(x)=9 m^2+2 m+3>0$
Bước 2: Tính $\Delta$ và chỉ ra dấu của $\Delta$ âm
Bước 3: Áp dụng tính chất của tam thức bậc hai
Yêu cầu bài toán tương đương chứng minh $f(x)=9 m^2+2 m+3>0$ với mọi $m$
Tam thức có $\Delta=2^2-4.9 .3=-104<0$
Áp dụng định lí về dấu của tam thức bậc hai ta có
$\Delta0$ nên $f(x)$ cùng dấu với a với mọi $m$
Vậy $f(x)=9 m^2+2 m+3>0$ với mọi $m \Leftrightarrow 9 m^2+2 m>-3$ với mọi $m$.
Bài tập 8 trang 10
a) $2 x^2+3 x+m+1>0$ với mọi $x \in \mathbb{R}$;
b) $m x^2+5 x-3 \leq 0$ với mọi $x \in \mathbb{R}$
a) Bước 1: Tính $\Delta$ và xác định dấu của $a$
Bước 2: $f(x)>0$ với mọi $x \in \mathbb{R}$ khi $a>0$ và $\Delta<0$
b) Bước 1: Tính $\Delta$ và xác định dấu của $a$
Bước 2: $f(x) \leq 0$ với mọi $x \in \mathbb{R}$ khi $a<0$ và $\Delta \leq 0$
a) Tam thức $2 x^2+3 x+m+1$ có $\Delta=3^2-4 \cdot 2 \cdot(m+1)=1-8 m$
Vì $a=2>0$ nên để $2 x^2+3 x+m+1>0$ với mọi $x \in \mathbb{R}$ khi và chỉ khi $\Delta<0 \Leftrightarrow 1-8 m\frac{1}{8}$
Vậy khi $m>\frac{1}{8}$ thì $2 x^2+3 x+m+1>0$ với mọi $x \in \mathbb{R}$
b) Tam thức $m x^2+5 x-3$ có $\Delta=5^2-4 \cdot m \cdot(-3)=25+12 m$
Đề $m x^2+5 x-3 \leq 0$ với mọi $x \in \mathbb{R}$ khi và chỉ khi $m<0$ và $\Delta=25+12 m \leq 0 \Leftrightarrow m \leq-\frac{25}{12}$
Vậy $m x^2+5 x-3 \leq 0$ với mọi $x \in \mathbb{R}$ khi $m \leq-\frac{25}{12}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài 1 Chương 7 Bất phương trình bậc hai một ẩn Toán 10 Chân trời sáng tạo tập 2 ở các trang 6, 7, 8, 9, 10. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





