Giải SGK Bài 2 Chương 6 trang 27, 28, 29, 30, 31, 32, 33, 34 Toán 10 Cánh diều tập 2
Ở bài viết lần này, HocThatGioi sẽ trả lời các câu hỏi và bài tập trong bài Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm. Đây là bài học thuộc Bài 2 Chương VI trang 27, 28, 29, 30, 31, 32, 33, 34 SGK Toán 10 Cánh diều tập 2. Hy vọng những lời giải chi tiết dưới đây sẽ giúp bạn hiểu và nắm rõ kiến thức cơ bản của bài học này.
Giải đáp câu hỏi SGK Bài 2 Chương 6 Toán 10 Cánh diều tập 2
Mở đầu bài học với các câu hỏi khởi động giúp bạn dễ dàng tiếp thu kiến thức về Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm.
Câu hỏi khởi động trang 27

Số bàn thắng trung bình trong mỗi trận đấu được tính như thế nào?
Số bàn thắng trung bình trong mỗi trận đấu được tính bằng tổng cộng số bàn thắng của tất cả các trận đấu rồi chia cho số trận đấu.
Số bàn thắng trung bình trong mỗi trận đấu:
= \frac{\mathrm{6+6+2+1+2+4+3} }{\mathrm{7} } =3,34
Hoạt động 1 trang 27
165 172 172 171 170
Tính trung bình cộng của 5 số trên.
Trung bình cộng của 5 số trên là:
\overline{X}= \frac{\mathrm{165+172+172+171+170} }{\mathrm{5} } =170
Luyện tập vận dụng 1 trang 27
Số bàn thắng trung bình trong mỗi trận đấu được tính bằng tổng cộng số bàn thắng của tất cả các trận đấu rồi chia cho số trận đấu.
Vì thế, khi cộng tất cả số bàn thắng của đội tuyển bóng đá nam trong 7 trận đấu rồi chia cho 7 ta được:
= \frac{\mathrm{6+6+2+1+2+4+3} }{\mathrm{7} } =3,34
Luyện tập vận dụng 2 trang 29
Tìm trung vị của mẫu số liệu trên.
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: 23 23 25 26
Bước 2: Mẫu số liệu có 4 số nên trung vị của mẫu số liệu là:
M_e = \frac{\mathrm{23+25} }{\mathrm{2} } =24 ({^o C} )
Luyện tập vận dụng 3 trang 31
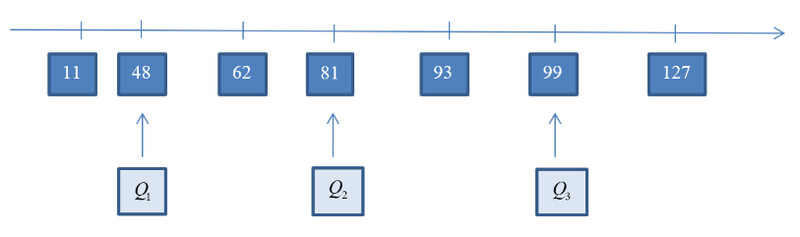
Biểu diễn tứ phân vị trên trục số.
Bước 2: Trung vị của mẫu số liệu là: 81
Bước 3: Trung vị của dãy số 11 48 62 là: 48
Bước 4: Trung vị của dãy số 93 99 127 là: 99
Bước 5: Vậy Q_1=48, Q_2=81, Q_3=99
Biểu diễn tứ phân vị trên trục số:
Hoạt động 4 trang 32
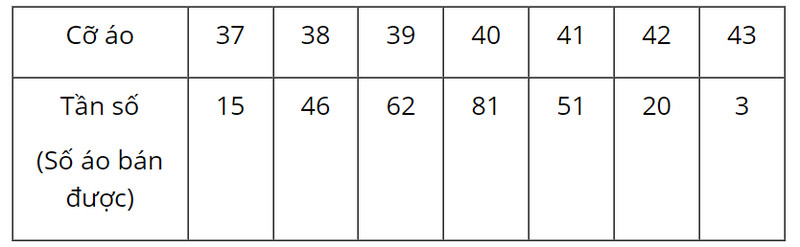
Cỡ áo nào cửa hàng bác Tâm bán được nhiều nhất trong tháng đầu tiên?
Cỡ áo mà cửa hàng bác Tâm bán được nhiều nhất trong tháng đầu tiên là cỡ áo: 40 (số áo bán được là 81).
Luyện tập vận dụng 4 trang 32
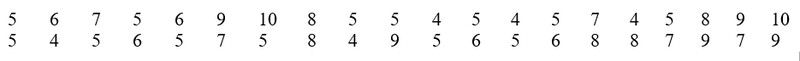
b) Tính tỉ lệ số học sinh lớp 10A đạt điểm từ 8 trở lên. Tỉ lệ đó phản ánh điều gì?

b) Để tính được tỉ lệ học sinh đạt từ 8 điểm trở lên, nhìn vào bảng ta thấy:
– Tần số học sinh đạt 8 điểm là 5
– Tần số học sinh đạt 9 điểm là 5
– Tần số học sinh đạt 10 điểm là 2
Vậy, tỉ lệ học sinh lớp 10A đạt 8 điểm trở lên là: \frac{\mathrm{5+5+2} }{\mathrm{40} } =0,3=30 \%
Tỉ lệ này cho thấy số học sinh đạt điểm giỏi của lớp 10A là 30 \%
Giải bài tập SGK Bài 2 Chương 6 Toán 10 Cánh diều tập 2
Sau khi tìm hiểu các hoạt động đầu mục và phần luyện tập vận dụng, chắc hẳn các bạn cũng đã nắm được kiến thức cơ bản về bài học Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm. Tiếp theo đây, cùng trả lời các câu hỏi trong phần bài tập SGK trang 33, 34 nhé.
Bài tập 1 trang 33
165 155 171 167 159 175 165 160 158
Đối với mẫu số liệu trên, hãy tìm:
a) Số trung bình cộng;
b) Trung vị;
c) Mốt;
d) Tứ phân vị.
a) Sử dụng định nghĩa số trung bình cộng
b) Sắp xếp mẫu số liệu theo thứ tự không giảm rồi sử dụng định nghĩa số trung vị
c) Lập bảng tần số rồi sử dụng định nghĩa mốt
d) Sắp xếp mẫu số liệu theo thứ tự không giảm rồi sử dụng định nghĩa tứ trung vị
a) Số trung bình cộng của mẫu số liệu trên là:
\overline{X}= \frac{\mathrm{165+155+171+167+159+175+165+160+158} }{\mathrm{9} } =163,9
b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
155 158 159 160 165 165 167 171 175
Vậy mẫu số liệu trên có trung vị là M_e =165

d) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
155 158 159 160 165 165 167 171 175
Mẫu số liệu trên có 9 số liệu nên số trung vị là: M_e =165
– Trung vị của dãy số 155 158 159 160 là: Q_1 = \frac{\mathrm{158+159} }{\mathrm{2} } =158,2
– Trung vị của dãy số 165 167 171 175 là: Q_2 = \frac{\mathrm{167+171} }{\mathrm{2} } =169
Vậy Q_1=158,2; Q_2=165; Q_3=169
Bài tập 2 trang 34

b) Cửa hàng đó nên nhập về nhiều hơn cỡ giày nào để bán trong tháng tiếp theo?
a) Ta thấy tần số lớn nhất là 70 và 70 ứng với cỡ giày 40 nên mốt của mẫu số liệu là: M_o =40
b) Do mốt là 40 nên cửa hàng đó nên nhập về nhiều hơn cỡ giày 40 để bán trong tháng tiếp theo.
Bài tập 3 trang 34

b) Nhiệt độ trung bình của tháng có giá trị thấp nhất là bao nhiêu độ C? Cao nhất là bao nhiêu độ C?
a) Nhiệt độ trung bình trong năm ở Hà Nội là:
\overline{X} = \frac{\mathrm{16,4+17,0+20,2+23,7+27,3+28,8+28,9+28,2+27,2+24,6+21,4+18,2} }{\mathrm{12} } =23,5
b)Nhiệt độ trung bình của tháng có giá trị thấp nhất là: 16,4 ({^o C} )
Nhiệt độ trung bình của tháng có giá trị cao nhất là: 28,9 ({^o C} )
Bài tập 4 trang 34

b) Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị thấp nhất là bao nhiều triệu héc-ta? Cao nhất là bao nhiêu triệu héc-ta?
c) So với năm 2008, tỉ lệ tổng diện tích rừng của nước ta năm 2019 tăng lên được bao nhiêu phần trăm? Theo em, tỉ lệ tăng đó là cao hay thấp?
d) Hãy tìm hiểu số liệu về tổng diện tích rừng của tỉnh em đang sống trong một số năm gần đây.
a) Diện tích rừng trung bình của nước ta từ năm 2008 đến năm 2019 là:
\overline{X}= \frac{\mathrm{13,1+13,2+13,4+13,5+13,9+14,0 +13,8+14,1+14,4+14,4+14,5+14,6} }{\mathrm{12} } =13,9
b) Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị thấp nhất là: 13,1 (triệu ha)
Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị cao nhất là: 14,6 (triệu ha)
c) So với năm 2008, tổng diện tích rừng của nước ta năm 2019 tăng lên số héc-ta là:
\Delta =14,6-13,1=1,5 (triệu ha)
Vậy so với năm 2008, tỉ lệ tổng diện tích rừng của nước ta năm 2019 tăng lên được:
\frac{\mathrm{1,5} }{\mathrm{13,1} } =11,4 \%
Theo đó ta có thể thấy rằng tỉ lệ tăng này là cao.
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Giải SGK Bài 2 Chương VI trang 27, 28, 29, 30, 31, 32, 33, 34 Toán 10 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 10 – Toán – Các số đặc trưng đo xu thế trung tâm
- Giải mục 1 trang 27, 28 SGK Toán 10 Cánh Diều tập 2
- Giải mục 2 trang 28, 29 SGK Toán 10 Cánh diều tập 2
- Giải SGK bài 13 chương V trang 78, 79, 80, 81, 82, 83 Toán 10 Kết nối tri thức tập 1
- Giải SGK Bài 3 Chương 6 trang 35, 36, 37, 38, 39, 40, 41 Toán 10 Cánh diều tập 2
- Giải SGK bài 3 chương VI trang 112, 113, 114, 115, 116, 117, 118, 119 Toán 10 Chân trời sáng tạo tập 1





