Giải SGK bài Ba đường Conic Toán 10 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Ba đường Conic. Các bài tập sau đây thuộc bài 4 chương 9 Sách giáo khoa Toán 10 Chân trời sáng tạo tập 2 ở các trang 64, 65, 66, 67, 68, 69, 70, 71, 73. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Ba đường Conic Toán 10 Chân trời sáng tạo
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động khởi động, khám phá, thực hành và vận dụng ở các trang 64, 65, 66, 67, 68, 69, 70 trong bài Ba đường Conic sách Toán 10 Chân trời sáng tạo một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
Hoạt động khởi động trang 63
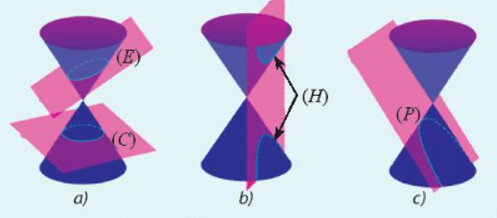
Qua bài học ta thấy rằng hình dạng của các đường là phương trình chính tắc của chúng như sau:
(E) có tên gọi là elip, phương trình: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
(H) có tên gọi là hypebol, phương trình: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
(P) có tên gọi là parabol, phương trình: $y^2=2 p x$
Hoạt động khám phá 1
Hinh 1 Tính tổng hai khoảng cách $F_{1} M$ và $F_{2} M$.
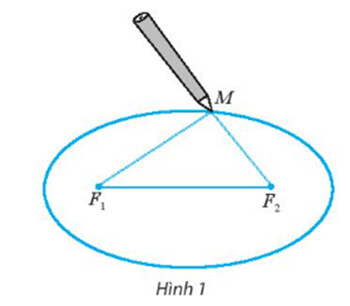
Ta có chiều dài vòng dây là:
M F_1+F_1 F_2+F_2 M=2 a+2 c \Rightarrow M F_1+F_2 M=2 a+2 c -F_1 F_2=2 a
Vậy tổng khoảng cách $F_1 M$ và $F_2 M$ là $2 a$
Hoạt động khám phá 2
Xét điểm $M(x ; y)$.
a) Tính $F_{1} M$ và $F_{2} M$ theo $x, y$ và $c$.
b) Giải thích phát biểu sau:
$M(x ; \mathrm{y}) \in(E) \Leftrightarrow \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2 a$.
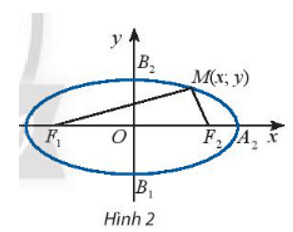
Sử dụng phương pháp tọa độ trong mặt phẳng
a) Ta có:
\overrightarrow{F_1 M}=(x+c ; y) \Rightarrow F_1 M=\sqrt{(x+c)^2+y^2} \\ \overrightarrow{F_2 M}=(x-c ; y) \Rightarrow F_2 M=\sqrt{(x-c)^2+y^2}
b) Ta có $M(x ; y) \in(E)$ nên
F_1 M+F_2 M=2 a \Leftrightarrow \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2 a
Thực hành 1 trang 65
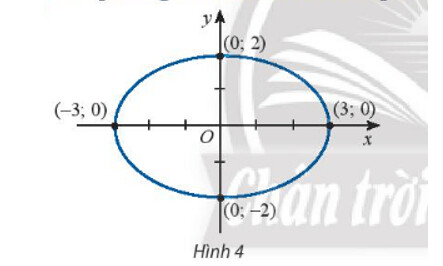
Phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với
M(x ; y) \in(E) ; b=\sqrt{a^2-c^2}
Dựa vào hình vẽ ta thấy a=3, c=2 \Rightarrow b=\sqrt{a^2-c^2}=\sqrt{3^2-2^2}=\sqrt{5}
Vậy phương trình chính tắc của elip có dạng $\frac{x^2}{9}+\frac{y^2}{5}=1$
Vận dụng 1 trang 65
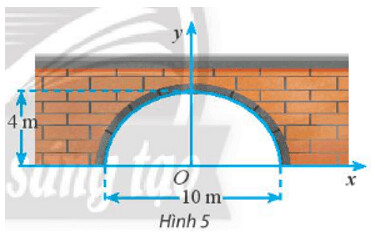
Phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với
M(x ; y) \in(E) ; b=\sqrt{a^2-c^2}
Chiều cao là $4 \mathrm{~m}$ tương ứng với $c=4$
Chiều rộng bằng $10 \mathrm{~m}$ nên $2 a=10 \Rightarrow a=5$
Suy ra $b=\sqrt{a^2-c^2}=\sqrt{5^2-4^2}=3$
Vậy phương trình chính tắc của elip có dạng $\frac{x^2}{25}+\frac{y^2}{9}=1$
Hoạt động khám phá 3 trang 65
Đính một đầu dây vào đầu $A$ của thước, dùng đinh ghim đầu dây còn lại vào điểm $F_{2}$. Đặt thước sao cho đầu $B$ của thước trùng với điểm $F_{1}$ và đoạn thẳng $B A$ có thể quay quanh $F_{1}$. Tựa đầu bút chì $M$ vào đoạn dây, di chuyển $M$ trên tấm bìa và giữ sao cho dây luôn căng, đoạn $A M$ ép sát vào thước, khi đó $M$ sẽ vạch ra trên tấm bia một đường $(H)$ (xem Hình 6b).
a) Chứng tỏ rằng khi $M$ di động, ta luôn có $M F_{1}-M F_{2}=2 a$.
b) Vẫn đính một đầu dây vào đầu $A$ của thước nhưng đổi chỗ cố định đầu dây còn lại vào $F_{1}$, đầu $B$ của thước trùng với $F_{2}$ sao cho đoạn thẳng $B A$ có thể quay quanh $F_{2}$ và làm tương tự như lần đầu để đầu bút chì $\mathrm{M}$ vẽ được một nhánh khác của đường $(H)$ (Hình $6 \mathrm{c})$. Tính $M F_{2}-M F_{1}$.
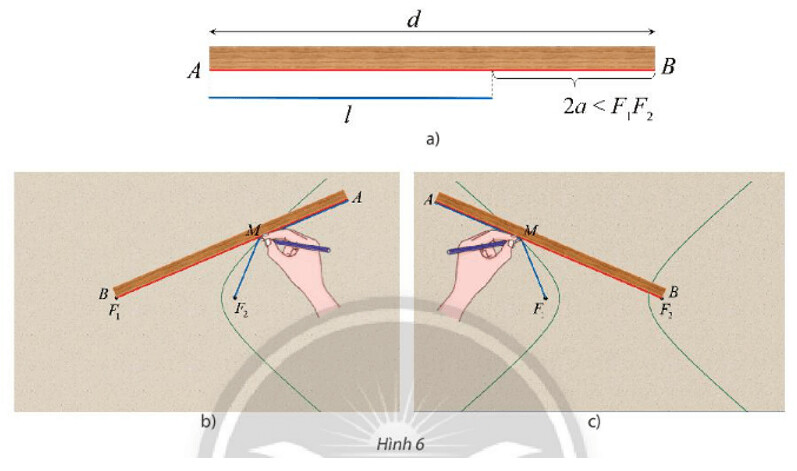
a) Khi điểm $M$ trùng với điểm $A$ ta có:
M F_1-M F_2=A F_1-A F_2=A B-A F_2=d-l=2 a
b) Tương tự khi điểm $M$ trùng với điểm $A$ ta có:
M F_2-M F_1=A F_2-A F_1=A B-A F_1=d-l=2 a
Hoạt động khám phá 4 trang 66
Xét điểm $M(x ; y)$.
a) Tính $F_{1} M$ và $F_{2} M$ theo $x, y$ và $c$.
b) Giải thích phát biểu sau:
$M(x ; \mathrm{y}) \in(H) \Leftrightarrow\left|\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right|=2 a$.
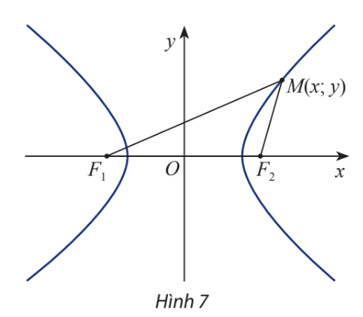
Sử dụng phương pháp tọa độ trong mặt phẳng
\overrightarrow{F_1 M}=(x+c ; y) \Rightarrow F_1 M=\sqrt{(x+c)^2+y^2} \\ \overrightarrow{F_2 M}=(x-c ; y) \Rightarrow F_2 M=\sqrt{(x-c)^2+y^2}
b) Ta có $M(x ; y) \in(E)$ nên
\left|F_1 M-F_2 M\right|=2 a \Leftrightarrow\left|\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}\right| =2 a
Thực hành 2 trang 67
Phương trình chính tắc của hypebol có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ với $M(x ; y) \in(H) ; b=\sqrt{c^2-a^2}$
Ta có: $2 c=10 \Rightarrow c=5,2 b=6 \Rightarrow b=3$
Suy ra $a=\sqrt{c^2-b^2}=\sqrt{5^2-3^2}=4$
Vậy phương trình chính tắc của hypebol có dạng $\frac{x^2}{16}-\frac{y^2}{9}=1$
Vận dụng 2 trang 67
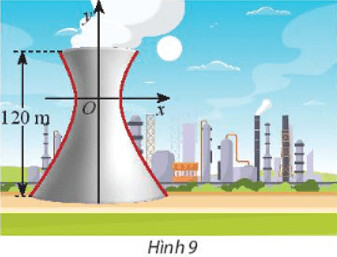
Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp
Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)
Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là $z$
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là $2 z$
Ta có $z+2 z=120 \Rightarrow z=40$
Thay $y=40$ vào phương trình $\frac{x^2}{27^2}-\frac{y^2}{40^2}=1$ ta tìm được $x=27 \sqrt{2}$
Thay $y=80$ vào phương trình $\frac{x^2}{27^2}-\frac{y^2}{40^2}=1$ ta tìm được $x=27 \sqrt{5}$
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là $27 \sqrt{2}$ và $27 \sqrt{5}$
Hoạt động khám phá 5 trang 68
Để tìm hệ thức giữa $x$ và $y$ sao cho $M$ cách đều $F$ và $\Delta$, một học sinh đã làm như sau:
– Tính $M F$ và $M H$ (với $H$ là hình chiếu của $M$ lên $\Delta$ ):
$M F=\sqrt{x^{2}+\left(y-\frac{1}{2}\right)^{2}}, M H=d(M, \Delta)=\left|y+\frac{1}{2}\right|$.
– Điều kiện để $M$ cách đều $F$ và $\Delta$ :
$M F=d(M, \Delta) \Leftrightarrow \sqrt{x^{2}+\left(y-\frac{1}{2}\right)^{2}}=\left|y+\frac{1}{2}\right|$.
$\Leftrightarrow x^{2}+\left(y-\frac{1}{2}\right)^{2}=\left(y+\frac{1}{2}\right)^{2}$
$\Leftrightarrow x^{2}=2 y \Leftrightarrow y=\frac{1}{2} x^{2}$.
Hãy cho biết tên đồ thị $(P)$ của hàm số $\left(^{*}\right)$ vừa tìm được.
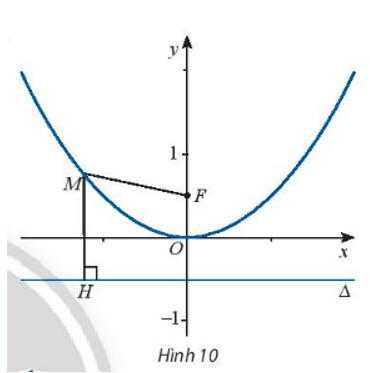
Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.
Hoạt động khám phá 6 trang 68
Gọi khoảng cách từ tiêu điểm đến đường chuẩn là $p$, hiển nhiên $p>0$.
Chọn hệ trục toạ độ $O x y$ sao cho $F\left(\frac{p}{2} ; 0\right)$ và $\Delta: x+\frac{p}{2}=0$.
Xét điểm $M(x ; y)$.
a) Tính $M F$ và $d(M, \Delta)$.
b) Giải thích phát biểu sau:
$M(x ; y) \in(P) \Leftrightarrow \sqrt{\left(x-\frac{p}{2}\right)^{2}+y^{2}}=\left|x+\frac{p}{2}\right|$.
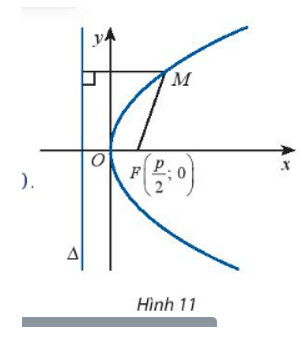
Sử dụng phương pháp tọa độ trong mặt phẳng
\text {a) Ta có: } \\ \overrightarrow{F M}=\left(x-\frac{p}{2} ; y\right) \Rightarrow M F=|\overrightarrow{F M}|=\sqrt{\left(x-\frac{p}{2}\right)^2+y^2} \\ d(M, \Delta)=\frac{\left|x+\frac{p}{2}\right|}{1}=\left|x+\frac{p}{2}\right|
b) $M$ thuộc parabol $(P)$ nên $M$ cách đều $F$ và $\Delta$
\text { Suy ra } M F=d(M, \Delta) \Leftrightarrow \sqrt{\left(x-\frac{p}{2}\right)^2+y^2}=\left|x-\frac{p}{2}\right|
Thực hành 3 trang 70
Bước 1: Từ phương trình đường chuẩn tìm tọa độ của tiêu điểm (phương trình đường chuẩn có dạng $x+\frac{p}{2}=0$
Bước 2: Viết phương trình chính tắc của parabol có dạng $y^2=2 p x$ với $M(x ; y) \in(P)$
Từ phương trình đường chuẩn $\Delta: x+1=0$ ta có tiêu điểm $F(1 ; 0)$
Phương trình chính tắc của parabol có dạng $y^2=2 x$
Vận dụng 3 trang 70
Bước 1: Gọi phương trình của parabol một cách tổng quát
Bước 2: Thay các giả thiết tìm tiêu điểm
Bước 3 : Thay $x=2$ vào phương trình chính tắc tìm $y$
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là $y^2=2 p x$
Ta có chiều cao của cổng $O H=B K=10$, chiều rộng tại chân cổng $B D=2 B H=5$
Vậy điểm $B$ có tọa độ là $B\left(10 ; \frac{5}{2}\right)$
Thay tọa độ điểm $B$ vào phương trình parabol ta có:
$\left(\frac{5}{2}\right)^2=2 p .10 \Rightarrow p=\frac{5}{16}$, suy ra phương trình parabol có dạng $y^2=\frac{5}{8} x$
Thay $x=2$ vào phương trình $y^2=\frac{5}{8} x$ ta tìm được $y=\frac{\sqrt{5}}{2}$
Vậy bề rộng của cổng tại chỗ cách đỉnh $2 \mathrm{~m}$ là $\sqrt{5} \mathrm{~m}$
Giải bài tập SGK bài Ba đường Conic Toán 10 Chân trời sáng tạo
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Ba đường Conic trang 70, 71, 73 sách Toán 10 Chân trời sáng tạo dưới đây nhé!
Bài 1 trang 70
a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16 ;
b) Hypebol có tiêu cự $2 c=20$ và độ dài trục thực $2 a=12$;
c) Parabol có tiêu điểm $F\left(\frac{1}{2} ; 0\right)$.
a)
Bước 1: Từ giải thiết xác định $a, b, c$
Bước 2: Phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với $M(x ; y) \in(E) ; b=\sqrt{a^2-c^2}$
b) Phương trình chính tắc của hypebol có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ với $M(x ; y) \in(H) ; b=\sqrt{c^2-a^2}$
c) Phương trình chính tắc của parabol có dạng $y^2=2 p x$ với $\backslash(\mathrm{M}(\mathrm{x} ; \mathrm{y}) \backslash i n$
a) Ta có $2 a=20 \Rightarrow a=10,2 c=16 \Rightarrow c=8$, suy ra $b=\sqrt{a^2-c^2}=\sqrt{10^2+8^2}=6$
Vậy phương trình chính tắc của elip có dạng $\frac{x^2}{100}+\frac{y^2}{36}=1$
b) Ta có $2 a=12 \Rightarrow a=6,2 c=20 \Rightarrow c=10$, suy ra $b=\sqrt{c^2-a^2}=\sqrt{10^2-6^2}=8$
Vậy phương trình chính tắc của elip có dạng $\frac{x^2}{100}-\frac{y^2}{64}=1$
c) Ta có tiêu điểm $F\left(\frac{1}{2} ; 0\right)$ suy ra $p=1$
Vậy phương trình chính tắc của parabol là $y^2=2 x$
Bài 2 trang 70
a) $\left(C_{1}\right): 4 x^{2}+16 y^{2}=1$
b) $\left(C_{2}\right): 16 x^{2}-4 y^{2}=144$
c) $\left(C_{3}\right): x=\frac{1}{8} y^{2}$.
Bước 1: Xác định dạng phương trình của đường conic nào
+) Có dạng $a x^2+b y^2=1$ là dạng đường elip
+) Có dạng $a x^2-b y^2=1$ là dạng đường hypebol
+) Có dạng $y^2=a x$ là dạng đường parabol
Bước 2: Đưa về phương trình chính tắc và tìm tọa độ biết phương trình chính tắc có dạng
+) $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ là đường elip
+) $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ là đường hypebol
+) $y^2=2 p x$ là đường parabol
Bước 3: Xác định tiêu điểm của các đường conic
+) Elip: $F_1(-c ; 0)$ và $F_2(c ; 0)$
+) Hypebol: $F_1(-c ; 0)$ và $F_2(c ; 0)$
+) Parabol: $F\left(\frac{p}{2} ; 0\right)$
a) Ta thấy phương trình có dạng $a x^2+b y^2=1$ nên phương trình $\left(C_1\right): 4 x^2+16 y^2=1$ là phương trình của đường elip
Từ phương trình $\left(C_1\right): 4 x^2+16 y^2=1$ ta có phương trình chính tắc là $\left(C_1\right): \frac{x^2}{\frac{1}{4}}+\frac{y^2}{\frac{1}{16}}=1$
Từ phương trình chính tắc ta có:
a=\frac{1}{2}, b=\frac{1}{4} \Rightarrow c=\sqrt{a^2-b^2}=\sqrt{\left(\frac{1}{2}\right)^2-\left(\frac{1}{4}\right)^2} =\frac{\sqrt{3}}{4}
Suy ra tiêu điểm của elip này là $F_1\left(-\frac{\sqrt{3}}{4} ; 0\right)$ và F_2\left(\frac{\sqrt{3}}{4} ; 0\right)
b) Ta thấy phương trình có dạng $a x^2-b y^2=1$ nên phương trình $\left(C_2\right): 16 x^2-4 y^2=144$ là phương trình của đường hypebol
Từ phương trình $\left(C_2\right): 16 x^2-4 y^2=144$ ta có phương trình chính tắc là $\left(C_1\right): \frac{x^2}{9}-\frac{y^2}{16}=1$
Từ phương trình chính tắc ta có: $a=3, b=4 \Rightarrow c=\sqrt{a^2+b^2}=\sqrt{3^2+4^2}=5$
Suy ra tiêu điểm của hypebol này là $F_1(-5 ; 0)$ và $F_2(5 ; 0)$
c) Phương trình $\left(C_3\right): x=\frac{1}{8} y^2$ có dạng $y^2=a x$ nên phương trình này là phương trình của parabol
Ta có phương trình chính tắc là $y^2=8 x$
Từ phương trình chính tắc ta có: $2 p=8 \Rightarrow p=4$
Suy ra tiêu điểm là $F(2 ; 0)$
Bài 3 trang 70
Chuẩn bị:
– Hai cái đinh, một vòng dây kín không đàn hồi, bút chì. Thục hiện:
– Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh lên hai điểm đó trên tấm ván.
– Quàng vòng dây qua hai chiếc đinh và kéo căng tại một điểm $M$ nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm $M$ rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường elip. (Xem minh hoạ trong Hình 15).
Phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu xentimét và lấy vòng dây có độ dài là bao nhiêu?
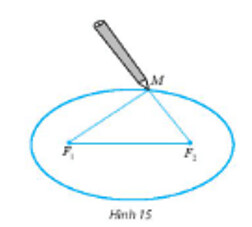
Bước 1: Từ giả thiết xác định $a, c$
Bước 2: Xác định vị trí đinh cách mép biết được tính bằng $a-c$
Bước 3: Xác định chiều dài vòng dây, biết chiều dài vòng dây là $2 a+2 c$
Từ giải thiết ta có:
2 a=80 \Rightarrow a=40,2 c=40 \Rightarrow c=20
Suy ra vị trí đinh cách mép là $a-c=40-20=20 \mathrm{~cm}$
Chiều dài vòng dây là $2 a+2 c=2.40+2.20=120 \mathrm{~cm}$
Vậy phải ghim hai cái đinh cách các mép tấm bìa $20 \mathrm{~cm}$ và lấy vòng dây có độ dài là $120 \mathrm{~cm}$
Bài 4 trang 71
a) Chọn hệ toạ độ thích hợp và viết phương trình của elip nói trên.
b) Tính khoảng cách theo phương thẳng đứng từ một điểm cách chân tường $5 \mathrm{~m}$ lên đến nóc nhà vòm.
a)
Bước 1: Chọn hệ trục tọa độ $O x y$ với gốc tọa độ tại tâm đáy nhà vòm
Bước 2: Viết phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với $M(x ; y) \in(E) ; b=\sqrt{a^2-c^2}$
b)
Bước 1: Từ dữ kiện cách chân tường $5 \mathrm{~m}$, xác định cách gốc tạo độ bao nhiêu $(x=$ ?)
Bước 2: Thay $x$ vừa tìm được vào phương trình chính tắc tìm $y$
a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng
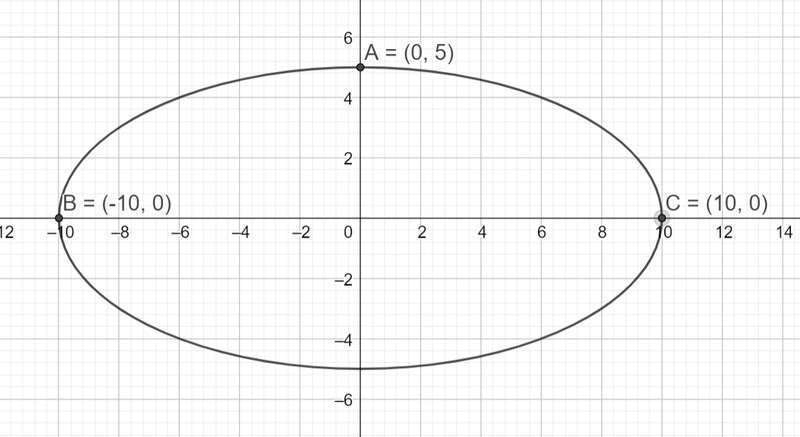
Nhà vòm có dạng elip nên có phương trình chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad$ (với $\left.a, b>0\right)$
Ta có chiều cao $8 \mathrm{~m}$ nên $O A=h=5$, chiều rộng của vòm là $20 \mathrm{~m}$, suy ra $B C=2 O B=20 \Rightarrow O B=10$
Từ đó ta có tọa độ các điểm: $C(10 ; 0), A(0 ; 5)$
Thay hai điểm đó vào phương trinh chính tắc ta có:
\left\{\begin{array} { l } { \frac { 1 0 ^ { 2 } } { a ^ { 2 } } + \frac { 0 ^ { 2 } } { b ^ { 2 } } = 1 } \\ { \frac { 0 ^ { 2 } } { a ^ { 2 } } + \frac { 5 ^ { 2 } } { b ^ { 2 } } = 1 } \end{array} \Rightarrow \left\{\begin{array}{l} a=10 \\ b=5 \end{array}\right.\right.
Suy ra, phương trình miêu tả hình dáng nhà vòm là $\frac{x^2}{100}+\frac{y^2}{25}=1$
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm $5 \mathrm{~m}$ (vì từ tâm vòm đến tưởng là $10 \mathrm{~m}$ )
Thay $x=5$ vào phương trình $\frac{x^2}{100}+\frac{y^2}{25}=1$, ta tìm được $y=\frac{5 \sqrt{3}}{2}$
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường $5 \mathrm{~m}$ đến nóc nhà vòm là $\frac{5 \sqrt{3}}{2} \mathrm{~m}$
Bài 5 trang 71

Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp
Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)
Gọi khoảng cách từ tâm đối xứng đến đáy tháp là $z$
Suy ra khoảng cách từ tâm đối xứng đến nóc tháp là $\frac{2}{3} z$
Ta có $z+\frac{2}{3} z=150 \Rightarrow z=90$
Thay $y=90$ vào phương trình $\frac{x^2}{28^2}-\frac{y^2}{42^2}=1$ ta tìm được $x=4 \sqrt{274}$
Thay $y=60$ vào phương trình $\frac{x^2}{28^2}-\frac{y^2}{42^2}=1$ ta tìm được $x=4 \sqrt{149}$
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là $4 \sqrt{149} \mathrm{~m}$ và $4 \sqrt{274} \mathrm{~m}$
Bài 6 trang 71
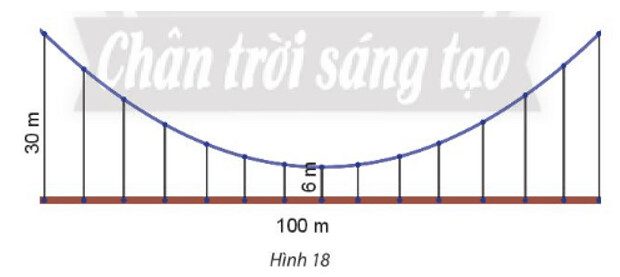
Bước 1: Gắn hệ trục tọa độ với gốc tọa độ tại điểm giữa cầu
Bước 2: Xác định phương trình mô tả hình dạng của cầu
Bước 3: Thay giả thiết vào phương trình vừa tìm được để tìm chiều dài thanh treo cầu
Chọn hệ tọa độ Oxy với gốc tọa độ tại điểm trên của thanh ngắn giữa cầu, trục tung tương ứng là mặt đường của cầu, vẽ lại hình như dưới đây
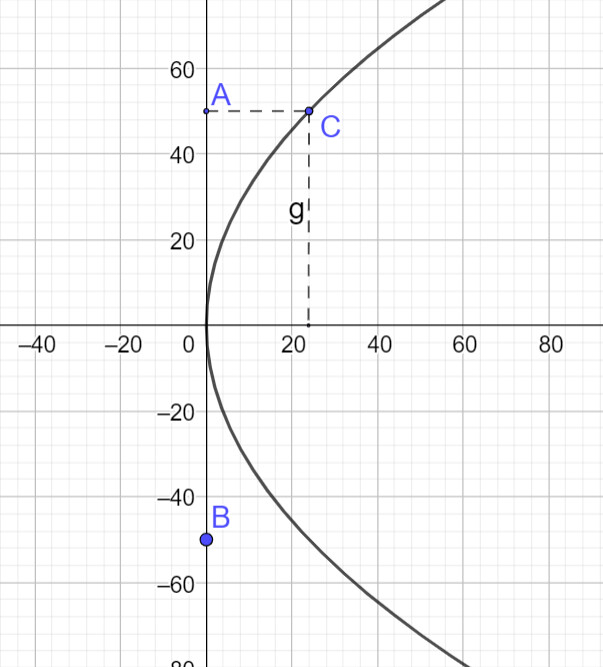
Ta nhận thấy cầu có dạng parabol nên gọi phương trình mô tả hình dạng cầu là $y^2=2 p x$
Cầu dài $100 \mathrm{~m}$ tương ứng $A B=2 O B=100 \Rightarrow O B=50$, thanh dài nhất dài 30 $\mathrm{m}$
Từ đó ta có tọa độ điểm $C(24 ; 50)$
Thay tọa độ $C$ vào phương trình $y^2=2 p x$ ta có $2500=2 p .24 \Rightarrow p=\frac{625}{12}$
Ta có phương trình mô tả cây cầu là $y^2=\frac{625}{6} x$
Tại thanh cách điểm giữa cầu $18 \mathrm{~m}$ thì $x=18$ ta có $18^2=\frac{625}{6} . x \Rightarrow x \approx 3,11$
Vậy chiều dài của thanh cách điểm giữa cầu $18 \mathrm{~m}$ gần bằng 3,11 m
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Ba đường Conic Toán 10 Chân trời sáng tạo tập 2 ở các trang 64, 65, 66, 67, 68, 69, 70, 71, 73. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





