SGK Toán 7 – Kết Nối Tri Thức
Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1
Các bài tập Luyện tập chung trang 74 SGK Toán 7 Kết nối tri thức sẽ giúp các bạn ôn tập lại các kiến thức về Tổng 3 góc tam giác và Trường hợp bằng nhau thứ nhất của 2 tam giác. Cùng xem HocThatGioi giải quyết các bài toán này nhé!
Bài 4.7 trang 69
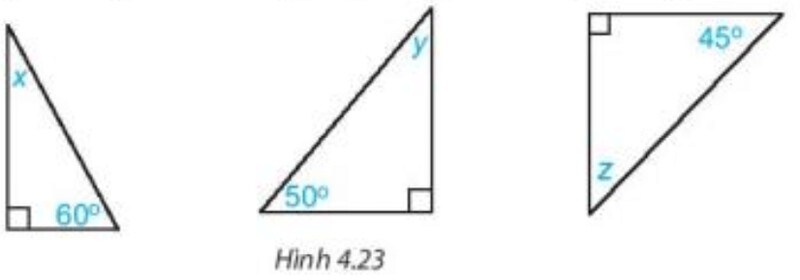
Các số đo $x, y, z$ trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?

Lời giải chi tiết:
Xét tam giác vuông trong hình đầu tiên ta có: $x+60^{\circ}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $x=90^{\circ}-60^{\circ}=30^{\circ}$.
Xét tam giác vuông trong hình thứ hai ta có: $y+50^{\circ}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $y=90^{\circ}-50^{\circ}=40^{\circ}$.
Xét tam giác vuông trong hình thứ ba ta có: $z+45^{\circ}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $z=90^{\circ}-45^{\circ}=45^{\circ}$.
Vậy $x=30^{\circ}, y=40^{\circ}, z=45^{\circ}$.
Xét tam giác vuông trong hình đầu tiên ta có: $x+60^{\circ}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $x=90^{\circ}-60^{\circ}=30^{\circ}$.
Xét tam giác vuông trong hình thứ hai ta có: $y+50^{\circ}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $y=90^{\circ}-50^{\circ}=40^{\circ}$.
Xét tam giác vuông trong hình thứ ba ta có: $z+45^{\circ}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $z=90^{\circ}-45^{\circ}=45^{\circ}$.
Vậy $x=30^{\circ}, y=40^{\circ}, z=45^{\circ}$.
Bài 4.8 trang 69
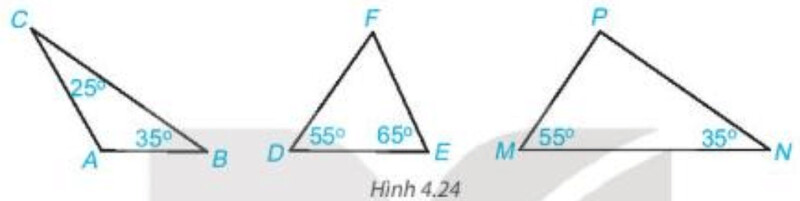
Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.

Lời giải chi tiết:
Xét tam giác $A B C$ có $\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$.
Do đó $\widehat{A}=180^{\circ}-\widehat{B}-\widehat{C}=180^{\circ}-35^{\circ}-25^{\circ}=120^{\circ}$.
Tam giác $A B C$ không có góc vuông nên tam giác $A B C$ không phải tam giác vuông. Xét tam giác $D E F$ có $\widehat{D}+\widehat{E}+\widehat{E}=180^{\circ}$.
Do đó $\widehat{F}=180^{\circ}-\widehat{D}-\widehat{E}=180^{\circ}-55^{\circ}-65^{\circ}=60^{\circ}$.
Tam giác $DEF$ không có góc vuông nên tam giác $DEF$ không phải tam giác vuông. Xét tam giác MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180^{\circ}$.
Do đó $\widehat{P}=180^{\circ}-\widehat{M}-\widehat{N}=180^{\circ}-55^{\circ}-35^{\circ}=90^{\circ}$.
Do đó góc $\mathrm{P}$ là góc vuông.
Tam giác $MNP$ có một góc vuông nên tam giác $MNP$ là tam giác vuông.
Xét tam giác $A B C$ có $\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$.
Do đó $\widehat{A}=180^{\circ}-\widehat{B}-\widehat{C}=180^{\circ}-35^{\circ}-25^{\circ}=120^{\circ}$.
Tam giác $A B C$ không có góc vuông nên tam giác $A B C$ không phải tam giác vuông. Xét tam giác $D E F$ có $\widehat{D}+\widehat{E}+\widehat{E}=180^{\circ}$.
Do đó $\widehat{F}=180^{\circ}-\widehat{D}-\widehat{E}=180^{\circ}-55^{\circ}-65^{\circ}=60^{\circ}$.
Tam giác $DEF$ không có góc vuông nên tam giác $DEF$ không phải tam giác vuông. Xét tam giác MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180^{\circ}$.
Do đó $\widehat{P}=180^{\circ}-\widehat{M}-\widehat{N}=180^{\circ}-55^{\circ}-35^{\circ}=90^{\circ}$.
Do đó góc $\mathrm{P}$ là góc vuông.
Tam giác $MNP$ có một góc vuông nên tam giác $MNP$ là tam giác vuông.
Bài 4.9 trang 69
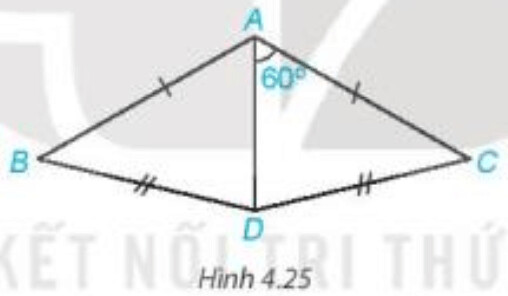
Cho Hình 4.25, biết $\widehat{D A C}=60^{\circ}, A B=A C, D B=D C$. Hãy tinh $\widehat{D A B}$.
Lời giải chi tiết:
Xét hai tam giác $ADB$ và $ADC$ có:
$A B=A C$ (theo giả thiết).
$\mathrm{BD}=\mathrm{CD}$ (theo giả thiết).
$AD$ chung.
Do đó $\triangle A \mathrm{D} B=\Delta A \mathrm{D} C(c-c-c)$.
Do đó $\widehat{D A B}=\widehat{D A C}$ (2 góc tương ứng).
Vậy $\widehat{D A B}=60^{\circ}$.
Xét hai tam giác $ADB$ và $ADC$ có:
$A B=A C$ (theo giả thiết).
$\mathrm{BD}=\mathrm{CD}$ (theo giả thiết).
$AD$ chung.
Do đó $\triangle A \mathrm{D} B=\Delta A \mathrm{D} C(c-c-c)$.
Do đó $\widehat{D A B}=\widehat{D A C}$ (2 góc tương ứng).
Vậy $\widehat{D A B}=60^{\circ}$.
Bài 4.10 trang 69
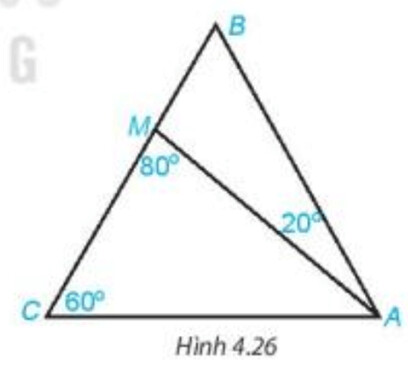
Cho tam giác $A B C$ có $\widehat{B C A}=60^{\circ}$ và điểm $\mathrm{M}$ nằm trên cạnh $\mathrm{BC}$ sao cho $\widehat{B A M}=20^{\circ}, \widehat{A M C}=80^{\circ}$ (H.4.26). Tính số đo các góc $\mathrm{AMB}$, $\mathrm{ABC}, \mathrm{BAC}$.
Lời giải chi tiết:
Xét tam giác $AMC$ có:
$\widehat{A M C}+\widehat{A C M}+\widehat{M A C}=180^{\circ}$.
Do đó $\widehat{M A C}=180^{\circ}-\widehat{A M C}-\widehat{A C M}=180^{\circ}-80^{\circ}-60^{\circ}=40^{\circ}$.
$\widehat{A M B}$ là góc ngoài tại đỉnh $\mathrm{M}$ của tam giác $AMC$ nên
$\widehat{A M B}=\widehat{A C M}+\widehat{M A C}=60^{\circ}+40^{\circ}=100^{\circ}$.
Xét tam giác $\mathrm{AMB}$ có $\widehat{A M B}+\widehat{M A B}+\widehat{A B M}=180^{\circ}$.
Do đó $\widehat{A B M}=180^{\circ}-\widehat{A M B}-\widehat{M A B}=180^{\circ}-100^{\circ}-20^{\circ}=60^{\circ}$.
hay $\widehat{A B C}=60^{\circ}$.
Ta có $\widehat{B A C}=\widehat{M A B}+\widehat{M A C}=20^{\circ}+40^{\circ}=60^{\circ}$.
Vậy $\widehat{A M B}=100^{\circ}, \widehat{A B C}=60^{\circ}, \widehat{B A C}=60^{\circ}$.
Xét tam giác $AMC$ có:
$\widehat{A M C}+\widehat{A C M}+\widehat{M A C}=180^{\circ}$.
Do đó $\widehat{M A C}=180^{\circ}-\widehat{A M C}-\widehat{A C M}=180^{\circ}-80^{\circ}-60^{\circ}=40^{\circ}$.
$\widehat{A M B}$ là góc ngoài tại đỉnh $\mathrm{M}$ của tam giác $AMC$ nên
$\widehat{A M B}=\widehat{A C M}+\widehat{M A C}=60^{\circ}+40^{\circ}=100^{\circ}$.
Xét tam giác $\mathrm{AMB}$ có $\widehat{A M B}+\widehat{M A B}+\widehat{A B M}=180^{\circ}$.
Do đó $\widehat{A B M}=180^{\circ}-\widehat{A M B}-\widehat{M A B}=180^{\circ}-100^{\circ}-20^{\circ}=60^{\circ}$.
hay $\widehat{A B C}=60^{\circ}$.
Ta có $\widehat{B A C}=\widehat{M A B}+\widehat{M A C}=20^{\circ}+40^{\circ}=60^{\circ}$.
Vậy $\widehat{A M B}=100^{\circ}, \widehat{A B C}=60^{\circ}, \widehat{B A C}=60^{\circ}$.
Bài 4.11 trang 69
Cho $\triangle A B C=\triangle D E F$. Biết rằng $\widehat{A}=60^{\circ}, \widehat{E}=80^{\circ}$, tính số đo các góc $B, C, D, F$.
Lời giải chi tiết:
Do $\triangle A B C=\triangle D E F$ nên ta có các cặp góc tương ứng bằng nhau:
$\widehat{A}=\widehat{D}=60^{\circ}, \widehat{B}=\widehat{E}=80^{\circ}, \widehat{C}=\widehat{F}$
Xét tam giác $\mathrm{ABC}$ có $\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$.
Do đó $\widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-60^{\circ}-80^{\circ}=40^{\circ}$.
Mà $\widehat{C}=\widehat{F}$ nên $\widehat{F}=40^{\circ}$.
Vậy $\widehat{B}=80^{\circ}, \widehat{D}=60^{\circ}, \widehat{C}=\widehat{F}=40^{\circ}$.
Do $\triangle A B C=\triangle D E F$ nên ta có các cặp góc tương ứng bằng nhau:
$\widehat{A}=\widehat{D}=60^{\circ}, \widehat{B}=\widehat{E}=80^{\circ}, \widehat{C}=\widehat{F}$
Xét tam giác $\mathrm{ABC}$ có $\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$.
Do đó $\widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-60^{\circ}-80^{\circ}=40^{\circ}$.
Mà $\widehat{C}=\widehat{F}$ nên $\widehat{F}=40^{\circ}$.
Vậy $\widehat{B}=80^{\circ}, \widehat{D}=60^{\circ}, \widehat{C}=\widehat{F}=40^{\circ}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương tam giác
- Giải SGK Bài tập cuối chương 7 trang 119, 120 Toán 7 Cánh diều tập 2
- Giải SGK Bài tập cuối chương 8 trang 84 Toán 7 Chân trời sáng tạo tập 2
- Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 9 trang 84 Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung trang 82, 83 SGK Toán 7 Kết nối tri thức Tập 2
- Giải SGK Luyện tập chung trang 86 Toán 7 Kết nối tri thức tập 1
- Giải luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2





