Khảo sát sự biến thiên và vẽ đồ thị của hàm số – đồ thị của một số hàm hay gặp nhất

Bài viết này, HocThatGioi sẽ hướng dẫn các bạn các bước khảo sát sự biến thiên và vẽ đồ thị của hàm số cơ bản hay gặp nhất, giúp các bạn có thể dễ dàng nhận dạng được các loại đồ thị khác nhau, nếu các bạn còn đang gặp vấn đề về dạng bài đồ thị này thì còn chần chừ gì nữa mà không cùng HocThatGioi bắt đầu bài học ngay bây giờ nào.

1. Các bước khảo sát sự biến thiên và vẽ đồ thị của hàm số y = f(x)

Bước 1: Tìm tập xác định D của hàm số.

Bước 2: Xét sự biến thiên:

*Xét sự biến thiên của hàm số

• Tìm đạo hàm bậc nhất y' ;
• Tìm các điểm tại đó y'=0 hoặc không xác định ;
• Xét dấu y' và suy ra chiều biến thiên của hàm số.

* Tìm cực trị.

* Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).

* Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị

Bước 3: Vẽ đồ thị

2. Tương giao của các đồ thị

Cho hai đồ thị (C_1):y=f(x)  và (C_2):y=g(x).

Phương trình xác định hoành độ giao điểm của (C_1) và (C_2) là:f(x)=g(x). (1)

• Nếu (1) vô nghiệm thì (C_1) và (C_2) không có điểm chung (không cắt nhau và không tiếp xúc với nhau).
• Nếu (1) có n nghiệm phân biệt thì (C_1)  và (C_2)  giao nhau tại n điểm phân biệt. Nghiệm của (1) chính là hoành độ các giao điểm.

3. Đồ thị của một số hàm hay gặp nhất

Đồ thị của các hàm số thường hay gặp trong đề thi:

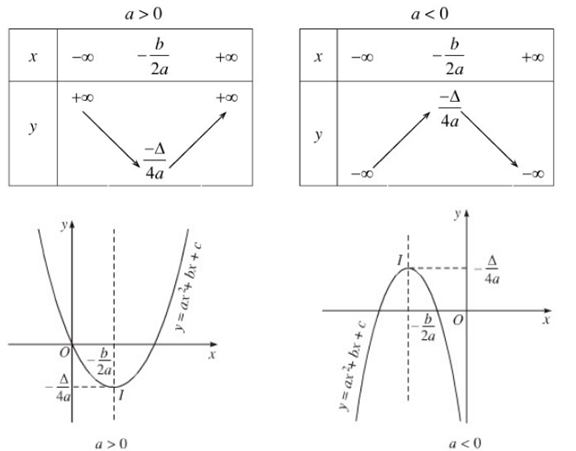
3.1 Hàm số đa thức bậc 2

Hàm số có dạng y=ax^2+bx+c(a\ne0) là 1 parabol có đỉnh là I(\frac{-b}{2a};\frac{-\Delta }{4a}) và trục đối xứng là x=\frac{-b}{2a}

• Đồ thị quay lên nếu a>0
• Đồ thị quay xuống nếu a<0

3.2 Hàm số đa thức bậc ba 

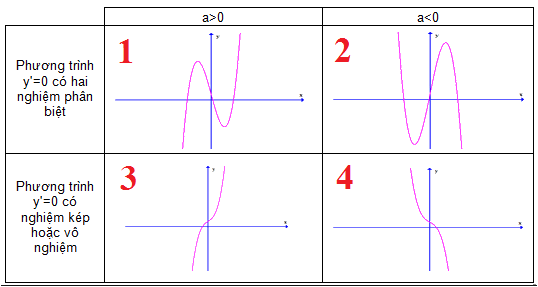
Hàm số có dạng y=ax^3+bx^2+cx+d(a\ne0) và có các tính chất sau:

• Cắt trục tung tại điểm có tung độ là d
• Cắt trục hoành tối đa tại 3 điểm.
• Đạo hàm: y′=3ax^2+2bx+c, \Delta'=b^2-3ac
• Hàm số có 2 cực trị nếu Δ′>0 và không có cực trị nếu Δ′≤0.
• Cực trị của hàm số x_1,x_2  thỏa mãn định lý Vi-ét: x_1+x_2=\frac{-2b}{3a} và x_1.x_2=\frac{c}{3a}

3.3 Hàm số đa thức bậc bốn trùng phương 

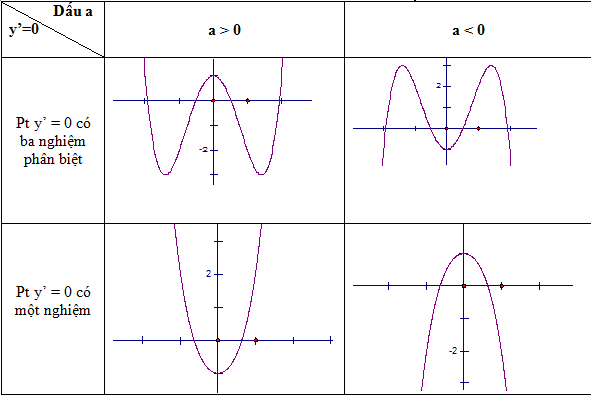
Hàm số có dạng f(x)=ax^4+bx^2+c(a\ne0) và có các tính chất sau:

• Cắt trục tung tại điểm có tung độ là c.
• Cắt trục hoành tối đa tại 4 điểm, các điểm này đối xứng lẫn nhau qua gốc O
• Đồ thị cắt trục hoành khi và chỉ khi \Delta=b^2−4ac>0
• y′=4ax^3+2bx=2x(2ax^2+b) . Hàm số luôn có 1 cực trị là x=0. Nếu a,b  cùng dấu thì đây là cực trị duy nhất còn nếu a,b trái dấu thì hàm số có thêm hai cực trị đối xứng nhau qua O là x=\sqrt{\frac{-b}{2a}}
• Hàm số có trục đối xứng là trục tung.

3.4 Hàm số phân thức bậc nhất

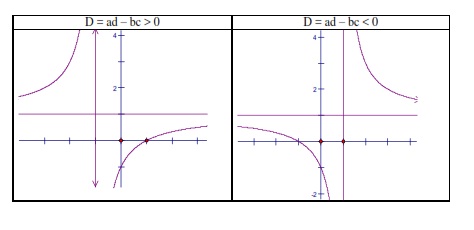
Hàm số có dạng y=\frac{ax+b}{cx+d} và có các tính chất sau:

• Cắt trục tung tại điểm có tung độ (0;\frac{b}{d})
• Cắt trục hoành tại điểm có hoành độ \frac{-b}{a}
• Tiệm cận ngang: y=\frac{a}{c}
• Tiệm cận đứng: x=\frac{-d}{c}
• f'(x)=\frac{ad-bc}{(cx+d)^2}

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Khảo sát sự biến thiên và vẽ đồ thị của hàm số và đồ thị của một số hàm hay gặp nhất. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!

Bài viết khác liên quan đến Lớp 12 – Toán – Khảo sát sự BT và vẽ ĐT

• Khảo sát sự biến thiên và vẽ đồ thị chương hàm số cực đầy đủ và chi tiết