Hàm số luỹ thừa hàm số mũ và hàm số logarit chi tiết nhất
Lý thuyết về hàm số luỹ thừa, hàm số mũ và hàm số logarit chi tiết. Cách nhận dạng, đạo hàm và tính chất, đồ thị của các hàm số này
Bài viết này, HocThatGioi sẽ giới thiệu với các bạn 3 loại hàm trọng tâm trong chương này là hàm số luỹ thừa, hàm số mũ, và hàm logarit, các lý thuyết cần phải lưu ý, cách đạo hàm và các tính chất bắt buộc phải nhớ của các loại hàm này. Nếu các bạn còn lơ mơ, chưa có được cái nhìn tổng quát về các loại hàm này thì đây sẽ là nơi giúp bạn thực hiện được điều đó. Hãy cùng HocThatGioi bắt đầu bài học ngay nào!
1. Lý thuyết hàm số luỹ thừa
Nắm rõ các lý thuyết hàm số lũy thừa dưới đây sẽ giúp bạn giải các bài tập hàm số lũy thừa một cách dễ dàng
1.1 Định nghĩa
Hàm số luỹ thừa là hàm số có dạng: y=x^a(a\in \mathbb{R})
1.2 Tập xác định
Hàm số y=x^a(a\in \mathbb{R}) có TXĐ phụ thuộc vào a:
- Với a nguyên dương: D=R
- Với a nguyên âm hoặc bằng 0: D=R\{0}
- Với a >0 và a không nguyên D=(0;+\infty)
1.3 Đạo hàm
Hàm số y=x^a(a\in \mathbb{R}) có đạo hàm với mọi x là: y'=ax^{a-1}
1.4 Tính chất cần lưu ý và đồ thị của hàm số luỹ thừa
Các tính chất cần lưu ý:
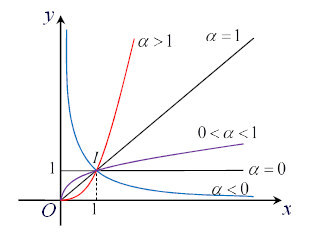
- Đồ thị luôn đi qua điểm (1;1)
- Khi a>0, hàm số luôn đồng biến, đồ thị hàm số không có tiệm cận
- Khi a<0, hàm số luôn nghịch biến, có tiệm cận đứng là Oy, tiệm cận ngang là Ox
Đồ thị của hàm số lũy thừa:
2. Lý thuyết hàm số mũ
Dưới đây là định nghĩa, tập xác định, đạo hàm, các tính chất cần lưu ý và đồ thị của hàm số mũ:
2.1 Định nghĩa
Hàm số mũ là hàm số có dạng: y=a^x(0<a\ne1)
2.2 Tập xác định
Hàm số mũ có tập xác định D=R và có tập giá trị là (0;+\infty)
2.3 Đạo hàm
Hàm số y=a^x(0<a\ne1) có đạo hàm với mọi x
y'=a^x.lna, đặc biệt (e^x)'=e^x
2.4 Tính chất cần lưu ý và đồ thị hàm số mũ
Tính chất cần lưu ý:
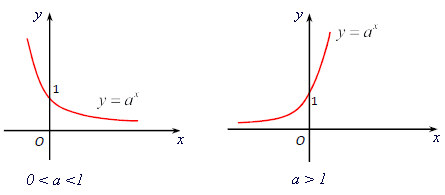
- Khi 0<a<1 hàm số nghịch biến
- Khi a>1 hàm số đồng biến
Đồ thị hàm số:
- Đồ thị hàm số mũ luôn nhận trục Ox là tiệm cận ngang.
- Luôn đi qua 2 điểm cố định là (0;1) và (1;a).
- Đồ thị hàm số luôn nằm phía trên trục hoành.
3. Lý thuyết hàm số logarit
Dưới đây là định nghĩa, tập xác định, đạo hàm, các tính chất cần lưu ý và đồ thị của hàm số logarit:
3.1 Định nghĩa
Hàm số logarit là hàm số có dạng: y=log_{a}^{x}(0<a\ne1)
3.2 Tập xác định
TXĐ của hàm số logarit D=(0;+\infty)
Hàm số logarit có tập giá trị là R
3.3 Đạo hàm
Hàm số y=log_{a}^{x}(0<a\ne1) có đạo hàm với mọi x >0:
y'=\frac{1}{xlna} , đặc biệt (lnx)'=\frac{1}{x}
3.4 Tính chất cần lưu ý và đồ thị hàm số logarit
Tính chất cần lưu ý:
- Khi a>1 , hàm số đồng biến
- Khi 0<a<1, hàm số nghịch biến
Đồ thị hàm số:
- Đồ thị hàm số có tiệm cận đứng là Oy
- Luôn đi qua 2 điểm cố định là (1;0) và (a;1)
- Nằm bên phải trục tung
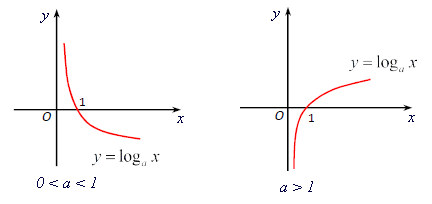
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết hàm số luỹ thừa, hàm số mũ và hàm số logarit chi tiết nhất. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!





