Lý thuyết Luỹ thừa – Hàm số luỹ thừa chi tiết và đầy đủ nhất

Quang Thái Tháng Mười Hai 6, 2021

Xin chào các bạn, hôm nay chúng ta sẽ bước vào một chương mới trong Đại số 12 và chuyên đề chúng ta nghiên cứu đầu tiên là Luỹ thừa, HocThatGioi sẽ đem đến cho các bạn đầy đủ lý thuyết luỹ thừa dễ hiểu nhất. Hãy cùng HocThatGioi bắt đầu buổi học hôm nay nhé.

1. Khái niệm luỹ thừa

Luỹ thừa là một phép toán học, được viết dưới dạng $a^{n}$ bao gôm hai số : cơ số $a$ và số mũ hoặc luỹ thừa $n$

1.1 Luỹ thừa số mũ nguyên dương

Cho $n$ là một số nguyên dương.

Với $a$ là số thực tuỳ ý, luỹ thừa bậc $n$ của $a$ là tích của $n$ thừa số $a$

Luỹ thừa bậc

n

của

a

a^{n} = a . a . a … .a

(

n

thừa số)

Trong đó:

a^{n}

: luỹ thừa bậc của a

n

: là một số nguyên dương (

n > 1

)

a

: là số thực tuỳ ý

Lưu ý: Với

a \neq 0

, ta có

a^{0} = 1

1.2 Luỹ thừa số mũ nguyên âm

Luỹ thừa số mũ nguyên âm

a^{-n} = \frac{1}{a^{n}}

Trong đó:

n

: là một số nguyên dương.

a

: là số thực (a \neq 0)

1.3 Luỹ thừa số mũ hữu tỷ

Cho số thực $a$ dương và số hữu tỉ $r = \frac{m}{n}$ . Luỹ thừa của $a$ với số mũ $r$ được xác định bởi :

Luỹ thừa số mũ hữu tỷ

a^{r} = a^{\frac{m}{n}} = \sqrt [n]{a^{m}}

Trong đó:

a

: số thực dương

r = \frac{m}{n}

: số hữu tỉ với

m \in \mathbb{Z}, n \in \mathbb{N}, n \geq 2

1.4 Luỹ thừa số mũ vô tỷ

Cho $a$ là một số dương, $\alpha$ là một số vô tỉ. Ta thừa nhận rằng luôn có một dãy số hữu tỉ $(r_{n})$ có giới hạn là $\alpha$ và dãy số tương ứng $(a^{r_{n}})$ có giới hạn không phụ thuộc vào việc chọn dãy số $(r_{n})$ .

Ta gọi giới hạn của dãy số $(a^{r_{n}})$ alf luỹ thừa của $a$ với số mũ $\alpha$ , kí hiệu là $a^{\alpha}$

Luỹ thừa số mũ vô tỷ

a^{\alpha} = \lim_{n \to +\infty} a^{r_{n}}

với

\alpha = \lim_{n \to +\infty} r_{n}

Trong đó:

a

là một số dương

\alpha

là một số vô tỉ

Lưu ý: Từ định nghĩa, ta có

1^{\alpha} = 1 (\alpha \in \mathbb{R}

1.5. Tính chất của luỹ thừa với số mũ thực

Luỹ thừa số mũ thực có các tính chất tương tự luỹ thừa với số mũ nguyên dương.

Cho $a, b$ là những số thực dương; $\alpha , \beta$ là những số thực tuỳ ý. Khi đó, ta có:

Tính chất của luỹ thừa với số mũ thực

a^{\alpha}.a^{\beta} = a^{\alpha + \beta}

\frac{a^{\alpha}}{a^{\beta}} = a^{\alpha – \beta}

(a^{\alpha})^{\beta} = a^{\alpha \beta}

(ab)^{\alpha} = a^{\alpha}b^{\alpha}

(\frac{a}{b})^{\alpha} = \frac{a^{\alpha}}{b^{\alpha}}

Nếu $a > 1$ thì $a^{\alpha} > a^{\beta}$ khi và chỉ khi $\alpha > \beta$ .

Nếu $a < 1$ thì $a^{\alpha} > a^{\beta}$ khi và chỉ khi $\alpha < \beta$ .

2. Lý thuyết hàm số luỹ thừa

Dưới đây là lý thuyết về khái niệm, tập xác định, đạo hàm,… của hàm số luỹ thừa

2.1 Khái niệm hàm số luỹ thừa

Hàm số luỹ thừa là hàm số $y = x^{\alpha}$ với $\alpha$ là số thực cho trước.

2.2 Tập xác định hàm số luỹ thừa

Tậm xác định của hàm số kuỹ thừa $y = x^{\alpha}$ tuỳ thuộc vào giá trị của $\alpha$ . Cụ thể :
Với $\alpha$ nguyên dương, tập xác định là $\mathbb{R}$
Với $\alpha$ nguyên âm hoặc bằng 0, tập xác định là $\mathbb{R}$ \ {0}
Với $\alpha$ không nguyên, tập xác định là Với $(0; +\infty)$

2.3 Đạo hàm của hàm số luỹ thừa

Hàm số luỹ thừa $y = x^{\alpha} (\alpha \in \mathbb{R})$ có đạo hàm với mọi $x > 0$ và

Đạo hàm hàm số luỹ thừa

(x^{\alpha})’ = \alpha x^{\alpha – 1}

2.3 Khảo sát hàm số luỹ thừa $y = x^{\alpha}$

Lý thuyết Luỹ thừa - Hàm số luỹ thừa chi tiết và đầy đủ nhất 3 — Khảo sát hàm số luỹ thừa $y = x^{\alpha}$

Lý thuyết Luỹ thừa - Hàm số luỹ thừa chi tiết và đầy đủ nhất 4 — Khảo sát hàm số luỹ thừa $y = x^{\alpha}$

$y = x^{\alpha}, \alpha > 0$	$y = x^{\alpha}, \alpha < 0$
Tập khảo sát : $(0; +\infty)$	Tập khảo sát : $(0; +\infty)$
Sự biến thiên: $y' = \alpha x^{\alpha - 1} > 0, \forall x > 0$	Sự biến thiên: $y' = \alpha x^{\alpha - 1} < 0, \forall x > 0$
Giới hạn đặc biệt : $\lim_{x \to 0^{+}}x^{\alpha} = 0, \lim_{x \to +\infty}x^{\alpha} = +\infty$	Giới hạn đặc biệt : $\lim_{x \to 0^{+}}x^{\alpha} = +\infty, \lim_{x \to +\infty}x^{\alpha} = 0$
Tiệm cận : Không có	Tiệm cân: Trục Ox là tiệm cận ngang Trục Oy là tiệm cận đứng của đồ thị
Bảng biến thiên: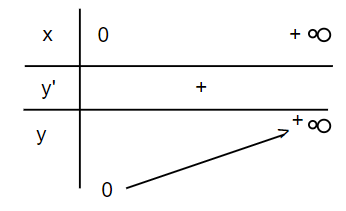	Bảng biến thiên: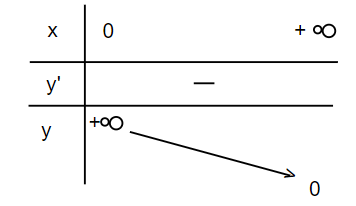

2.4 Đồ thì hàm số luỹ thừa $y = x^{\alpha}$

Đồ thị <span class="katex-eq" data-katex-display="false">y = x^{\alpha}</span> — Đồ thị $y = x^{\alpha}$

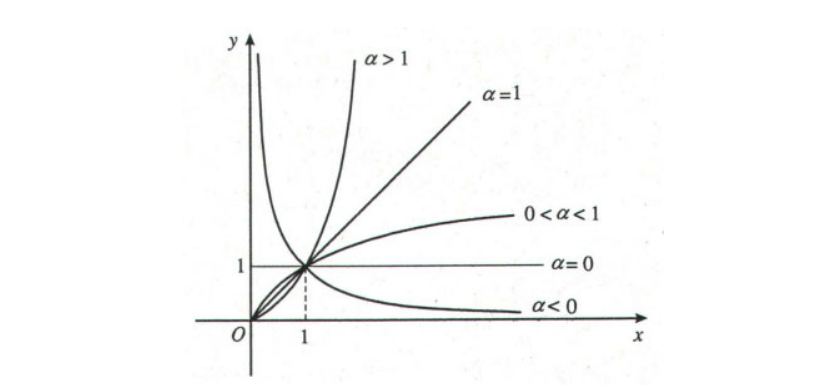
Đồ thị luôn đi qua điểm $(1;1)(1;1)$
Khi $\alpha > 0$ , hàm số luôn đồng biến
Khi $\alpha < 0$ hàm số luôn nghịch biến

Lưu ý: Khi khảo sát hàm số luỹ thừa với số mũ cụ thể, ta phải xét hàm số trên toàn bộ tập xác định của nó

Trên đây là bài viết về Lý thuyết Luỹ thừa chi tiết và đầy đủ nhất mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương hàm số mũ – hàm logarit để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt