Lý thuyết phép dời hình đầy đủ nhất
Xin chào các bạn, bài viết hôm nay sẽ tiếp tục giới thiệu tới các bạn khái niệm, tính chất,.. của phép dời hình. Hãy cùng HocThatGioi theo dõi hết bài viết để có thêm được những kiến thức mới. Cùng HocThatGioi bắt đầu buổi học hôm nay nhé.
1. Lý thuyết phép dời hình
Dưới đây là toàn bộ lý thuyết của phép dời hình
1.1 Định nghĩa
Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
– Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.
– Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình là một phép dời hình.
1.2 Tính chất
Phép dời hình:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
- Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
- Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.
- Biến đường tròn thành đường tròn có cùng bán kính.
– Xét phép dời hình F biến \Delta ABC thành \Delta A_{1}B_{1}C_{1} thì nó biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, nội tiếp của \Delta ABC tương ứng với trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, nội tiếp của \Delta A_{1}B_{1}C_{1}
– Phép dời hình F biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh tương ứng, biến cạnh thành cạnh.
– Hai hình được gọi là bằng nhau khi và chỉ khi có một phép dời hình biến hình này thành hình kia
1.3 Khái niệm hai hình bằng nhau
Hai hình bằng nhau được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
4. Bài tập phép dời hình
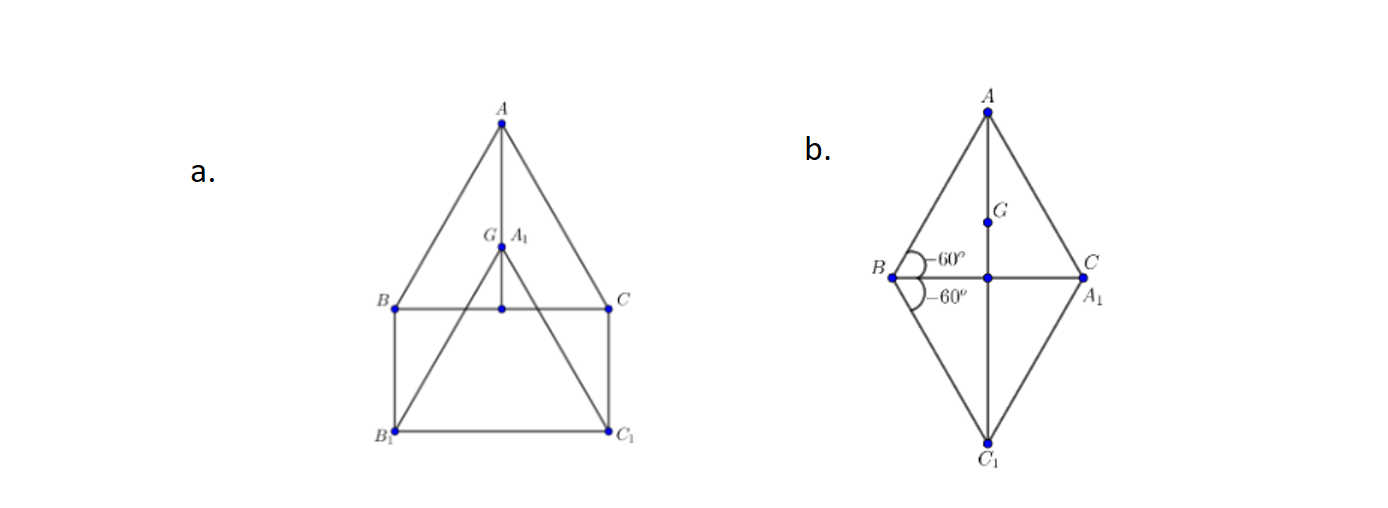
a. Qua T_{\overrightarrow{AG}}
b. Qua Q_{(B;-60^{\circ})}
Ta có:
T_{\overrightarrow{AG}}(A) = A_{1} \equiv G
T_{\overrightarrow{AG}}(B) = B_{1} \Leftrightarrow \overrightarrow{BB_{1}} = \overrightarrow{AG}
T_{\overrightarrow{AG}}(C) = C_{1} \Leftrightarrow \overrightarrow{CC_{1}} = \overrightarrow{AG}
Vậy T_{\overrightarrow{AG}}(\Delta ABC) = \Delta A_{1}B_{1}C_{1}
b. Qua Q_{(B;-60^{\circ})}
Q_{(B;-60^{\circ})}(B) = B
Q_{(B;-60^{\circ})}(A) = A_{1}, A_{1} \equiv C
Q_{(B;-60^{\circ})}(C) = C_{1}, C_{1} đối xứng với A qua BC
Vậy Q_{(B;-60^{\circ})}(\Delta ABC) = \Delta A_{1}BC_{1}
Khi đó d’ song song hoặc trùng d nên d’ : 3x – y + c = 0
Gọi A(1;0) \in d. Suy ra AA’ là đường cao của lăng trụ h = AA’ = 4a
Phép đối xứng tâm I(1;2) biến A(1;0) thành B(1;4)
Phép tịnh tiến theo vectơ \overrightarrow{v} = (-2;1) biến B(1;4) thành C(-1;5)
Mà C(-1;5) \in d’: 3x – y + c = 0 nên 3.(-1) – 5 + c = 0 \Rightarrow c = 8
Vậy d’: 3x – y + 8 = 0
Phép tịnh tiến theo vectơ \overrightarrow{u} = (-2;1) biến I(2;0) thành O(0;0)
Phép tịnh tiến theo vectơ \overrightarrow{v} = (1;3) biến O(0;0) thành I'(1;3)
Do đó, ảnh của (C) khi thực hiện liên tiếp phép tịnh tiến theo vectơ \overrightarrow{u} = (-2;1) và phép tịnh tiến theo vectơ \overrightarrow{v} = (1;3) là đường tròn (C)’ có tâm I'(1;3) và bán kính R = 1
Vậy (C’): (x – 1)^{2} + (y – 3)^{2} = 1
Trên đây là Lý thuyết phép dời hình đầy đủ nhất. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hi vọng rằng bài viết sẽ mang lại thêm các kiến thức về chương số phức cho bạn. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt!





