Phương trình đường tròn toán lớp 10
Phương trình đường tròn là phần kiến thức căn bản ở chương trình Toán lớp 10. Các bạn hãy cùng hocthatgioi đọc ngay bài viết dưới đây để củng cố và tìm hiểu thêm một số thông tin liên quan đến phần kiến thức này.
Phương trình đường tròn
Phương trình đường tròn có tâm I (a;b) , bán kính R: \left ( x-a \right )^{2}+ \left ( y-b \right )^{2}=R^{2}
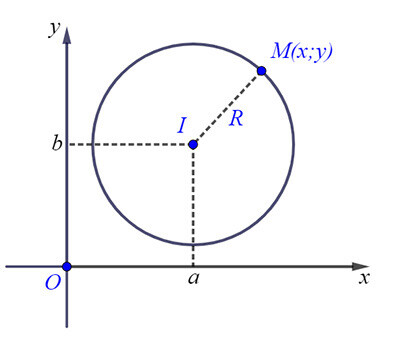
Cũng có thể viết phương trình đường tròn tâm I(a,b) và bán kính R=\sqrt{a^{2}+b^{2}-c} dướng dạng: x^{2}+y^{2}-2ax-2by+c=0 \left ( a^{2}+b^{2}-c> 0 \right )
Trong đó: c=a^{2}+b^{2}-R^{2}
Điều kiện để phương trình R=\sqrt{a^{2}+b^{2}-c} là phương trình đường tròn (C) phải thỏa mãn: a^{2}+b^{2}-c> 0. Khi đó đường tròn (C) có tâm I (a;b), bán kính R^{2}.
Cách viết phương trình đường tròn
Cách 1:
Cách 2:
Giả sử phương trình đường tròn (C) là: x^{2}+y^{2}-2ax-2by+c=0 hoặc x^{2}+y^{2}+2ax+2by+c=0
Cách viết phương trình tiếp tuyến của đường tròn
Cho điểm M_{0}\left ( x_{0};y_{0} \right ) nằm trên đường tròn (C), tâm I (a;b) . Gọi \Delta là tiếp tuyến của (C) tại M_{0}.
Ta có:
IM_{0}=\left ( x_{0}-a,y_{0}-b \right ) là vectơ pháp tuyến của \Delta.
Do đó, phương trình của \Delta là: \left (x_{o}-a \right )\left ( x-x_{0} \right )+\left ( y_{0}-b \right )\left ( y-y_{0} \right )=0
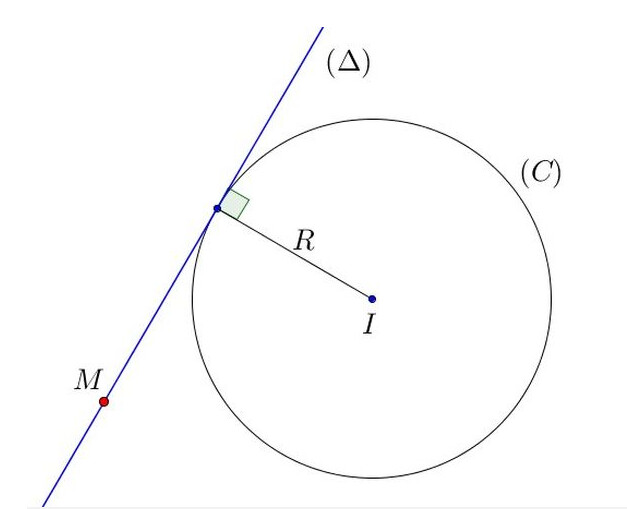
Vậy phương trình trên là phương trình tiếp tuyến của đường tròn \left ( x-a \right )^{2}+ \left ( y-b \right )^{2}=R^{2} tại điểm M_{0}\left ( x_{0};y_{0} \right ) nằm trên đường tròn.
Quan hệ giữa đường tròn với đường thẳng
Cho đường tròn (O;R) và một đường thẳng \Delta bất kỳ. Gọi d là khoảng cách từ tâm O của đường tròn đến đường thẳng đó.
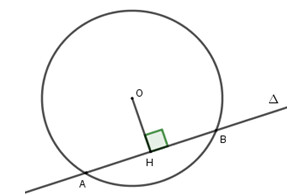
Trường hợp 1: Đường thẳng \Delta và đường tròn (O;R) cắt nhau.
Khi đó, đường thẳng và đường tròn có 2 điểm chung và khoảng cách d=OH<R
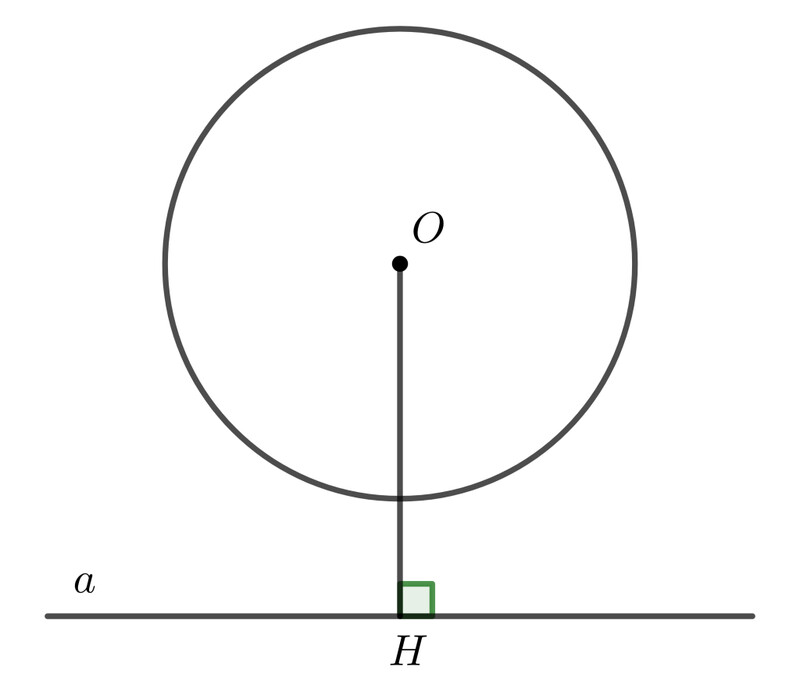
Trường hợp 2: Đường thẳng \Delta và đường tròn (O;R) tiếp xúc nhau.
Khi đó, đường thẳng và đường tròn có 1 điểm chung và khoảng cách d=OB=R
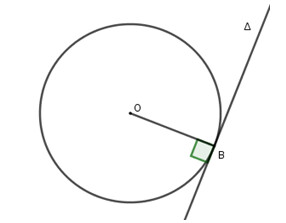
Đường thẳng \Delta được gọi là tiếp tuyến của đường tròn và B được gọi là tiếp điểm.
Trường hợp 3: Đường thẳng \Delta và đường tròn (O;R) không giao nhau.
Khi đó, đường thẳng và đường tròn không có điểm chung và khoảng cách d=OH>R.
Bài tập áp dụng
Bài 1 (trang 83 SGK Hình học 10):
Tìm tâm và bán kính của các đường tròn sau:
a. x^{2}+y^{2}-2x-2y-2=0
b. 16x^{2}+16y^{2}+16x-8y-11=0
c. x^{2}-y^{2}-4x+6y-3=0
Bài giải:
a. x^{2}+y^{2}-2x-2y-2=0 có hệ số a=1, b=1, c=-2
=> Tâm I(1;1) và bán kính R=\sqrt{1^{2}+1^{2}-\left ( -2 \right )}
b. 16x^{2}+16y^{2}+16x-8y-11=0
\Leftrightarrow x^{2}+y^{2}+x-\frac{1}{2}y-\frac{11}{6}=0 \Leftrightarrow x^{2}+y^{2}-2.\frac{-1}{2}.y-\frac{11}{16}=0Có a=\frac{-1}{2}, b=\frac{1}{4},c=\frac{-11}{16}
=> Đường tròn có tâm I\left ( \frac{-1}{2},\frac{1}{4} \right )
c. x^{2}-y^{2}-4x+6y-3=0
\Leftrightarrow x^{2}+y^{2}-2.2x-2.(-3).y-3=0=> a=2, b=-3, c=-3
=> Đường tròn có tâm I(2,-3), bán kính R=\sqrt{2^{2}-\left ( -3 \right)^{2}-\left ( -3 \right )}=4
Bài 2 (trang 83 SGK Hình học 10):
Lập phương trình đường tròn (C) trong các trường hợp sau:
a. (C) có tâm I(-2; 3) và đi qua M(2; -3)
b. (C) có tâm I(-1; 2) và tiếp xúc với đường thẳng x – 2y +7 =0
c. (C) có đường kính AB với A = (1; 1) và B = (7; 5)
Bài giải:
a. (C) có tâm I(-2; 3) và đi qua M(2; -3)
(C) có tâm I và đi qua M nên bán kính R = IM
Ta có:IM=\sqrt{\left ( x_{M}-x_{i} \right )^{2}+\left ( y_{M}-y_{i} \right )^{2}}=\sqrt{\left ( 2+2 \right )^{2}+\left ( -3-3 \right )^{2}}=\sqrt{52}
Vậy đường tròn (C): \left (x+2 \right )^{2}+\left ( y-3 \right )^{2}=52
b. (C) có tâm I(-1; 2) và tiếp xúc với đường thẳng \Deltax – 2y +7 =0
(C) tiếp xúc với \Delta : x – 2y +7 =0
=> d(I,\Delta)=R
Mà d\left ( I,\Delta \right )=\frac{\left| -1-2.2+7\right|}{\sqrt{1^{2}+\left ( -2 \right )^{2}}}=\frac{-2}{\sqrt{5}}
Vậy đường tròn (C): \left (x+1 \right )^{2}+\left ( y-2 \right )^{2}=\frac{4}{{5}}
c. (C) có đường kính AB với A = (1; 1) và B = (7; 5)
(C) có đường kính AB nên (C) có :
+ Tâm I là trung điểm của AB
=> I=\left ( \frac{x_{A}+x_{B}}{2},\frac{y_{A}+{y_{B}}}{2} \right ) hay I(4,3)
+ Bán kính R=\frac{AB}{2}=\frac{1}{2}\sqrt{\left ( 7-1 \right )^{2}+\left ( 5-1 \right )^{2}}=\sqrt{13}
Vậy đường tròn (C): \left (x-4 \right )^{2}+\left ( y-3 \right )^{2}=13
Trên đây là bài viết về Phương trình đường tròn toán lớp 10. Qua bài viết này, HocThatGioi hy vọng bạn có thể hiểu rõ và chính xác hơn về phương trình đường tròn. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt!





