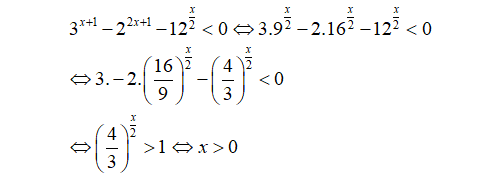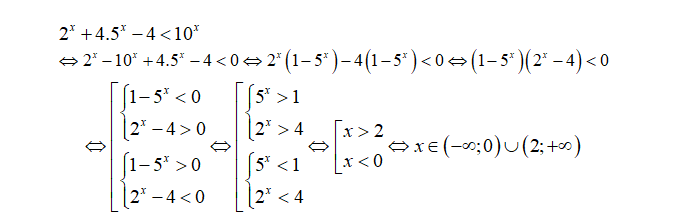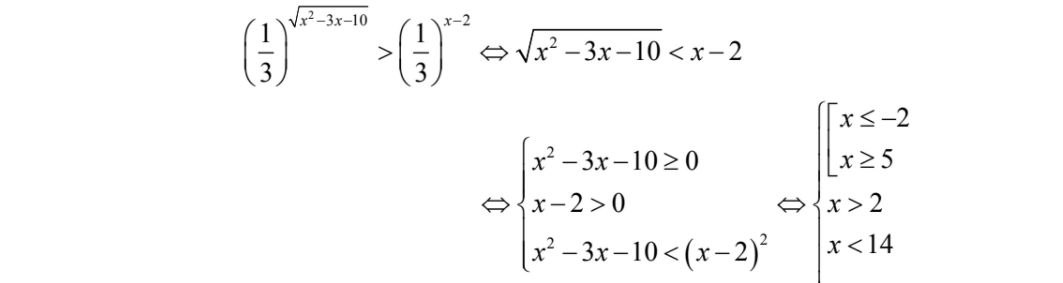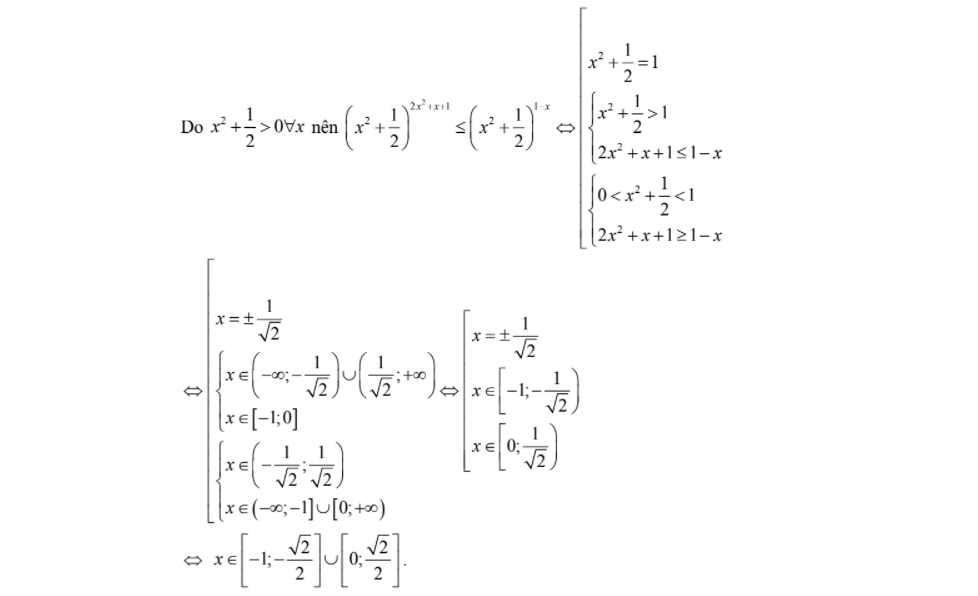10 câu bài tập bất phương trình mũ khó có lời giải chi tiết nhất

Quang Thái Tháng Mười Hai 23, 2021

Xin chào các bạn, sau khi hoàn thành bài Phương pháp giải – bài tập bất phương trình mũ, thì chắc các bạn đã nắm vững kiến thức cơ bản để giải một bài toán bất phương trình mũ. Vì vậy hôm nay HocThatGioi sẽ đem đến cho các bạn các câu bài tập bất phương trình ở mức vận dụng – vận dụng cao. Hãy theo dõi hết bài viết hôm nay nhé.

1. Tập nghiệm của bất phương trình

3^{x + 1} – 2^{2x + 1} – 12^{\frac{x}{2}} < 0

là:

a. $x \in (0;+\infty)$
b. $x \in (1;+\infty)$
c. $x \in (-\infty;0)$
d. $x \in (-\infty;1)$

2. Tập nghiệm của bất phương trình

\frac{2.3^{x} – 2^{x + 2}}{3^{x} – 2^{x}} \leq 1

là:

a. $x \in (0;\log_{\frac{3}{2}}3]$
b. $x \in (1;3)$
c. $x \in (1;3]$
d. $x \in [0;\log_{\frac{3}{2}}3]$

3. Tập nghiệm của bất phương trình

2^{x} + 4.5^{x} – 4 < 10^{x}

là:

a. $x 2$
b. $x < 0$
c. $x > 2$
d. $0 < x < 2$

4. Tập nghiệm của bất phương trình

2^{\sqrt{x}} – 2^{1 – \sqrt{x}} < 1

là:

a. $-1 \leq x \leq 1$
b. $-8 < x < 0$
c. $1 < x < 9$
d. $0 \leq x < 1$

5. Số nghiệm của bất phương trình

(\frac{1}{3})^{\sqrt{x^{2} – 3x = 10}} > (\frac{1}{3})^{x – 2}

là

a. 1
b. 0
c. 9
d. 11

6. Tập nghiệm của bất phương trình

(x^{2} + \frac{1}{2})^{2x^{2} + x + 1} \leq (x^{2} + \frac{1}{2})^{1 – x}

là

a. $[-1;\frac{-\sqrt{2}}{2}]$
b. $[0;\frac{\sqrt{2}}{2}]$
c. $(-1;0)$
d. $[-1;-\frac{\sqrt{2}}{2}] \smile [0;\frac{\sqrt{2}}{2}]$

7. Bất phương trình

(3^{x} – 1)(x^{2} + 3x – 4) > 0

có bao nhiêu nghiệm nguyên nhỏ hơn 6 ?

a. 9
b. 5
c. 7
d. Vô số

8. Cho bất phương trình:

\frac{1}{5^{x + 1} – 1} \geq \frac{1}{5 – 5^{x}}

. Tìm tập nghiệm của bất phương trình.

a. $S = (-1;0] \smile (1;+\infty)$
b. $S = (-1;0)$
c. $S = (-\infty;0]$
d. $S = (0;1)$

9. Bất phương trình

25^{-x^{2} + 2x + 1} + 9^{-x^{2} + 2x + 1} \geq 34.15^{-x^{2} + 2x}

có tập nghiệm là:

a. $S = (-\infty;1 – \sqrt{3}) \smile [0;2] \smile [1 + \sqrt{3};+\infty)$
b. $S = (0;+\infty)$
c. $S = (2;+\infty)$
d. $(1 – \sqrt{3};0)$

10. Với giá trị nào của tham số

m

thì bất phương trình

2^{sin^{2}x} + 3^{cos^{2}x \geq m.3^{sin^{2}x}}

có nghiệm ?

a. $m \leq 4$
b. $m \geq 4$
c. $m \leq 1$
d. $m \geq 1$

Trên đây là bài viết 10 câu bài tập bất phương trình mũ khó có lời giải chi tiết nhất. mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương Hàm số mũ – Hàm số logarit để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt.