Lý thuyết về mặt cầu – mặt cầu ngoại tiếp khối chóp
Lý thuyết về mặt cầu, vị trí tương đối của mặt cầu so với điểm, đường thẳng và mặt phẳng, mặt cầu ngoại tiếp khối chóp,...
Ở bài trước, chúng ta đã tìm hiểu về mặt nón và mặt trụ – 2 dạng của mặt tròn xoay, và hôm nay ta sẽ tiếp tục tìm hiểu về một dạng mặt tròn xoay nữa, đó chính là mặt cầu. Cùng với các Lý thuyết về mặt cầu ta sẽ tìm hiểu thêm về vị trí tương đối của điểm, đường, và mặt phẳng đối với mặt cầu – các kiến thức khá quan trọng để giải các bài toán về mặt cầu. Còn đợi gì nữa mà không cùng HocThatGioi bắt đầu bài học ngay nào!
1. Lý thuyết về mặt cầu
1.1 Định nghĩa mặt cầu
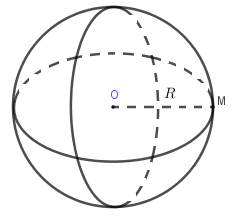
Mặt cầu tâm O bán kính R là tập hợp các điểm M trong không gian cách điểm O cố định một khoảng R không đổi.
Kí hiệu: S(O;R)=(M|OM=R)
Khối cầu tâm O bán kính R là tập hợp các điểm M thuộc mặt cầu và nằm trong mặt cầu.
Kí hiệu: V(O;R)=( M|OM≤R)
1.2 Diện tích mặt cầu và thể tích khối cầu
• Diện tích mặt cầu: S=4 \pi R^2
• Thể tích mặt cầu: V=\frac{4}{3} \pi R^3
2. Vị trí tương đối của mặt cầu với điểm, đường thẳng, mặt phẳng
2.1 Vị trí tương đối điểm so với mặt cầu
Cho mặt cầu S(O; R) và một điểm A bất kì, khi đó:
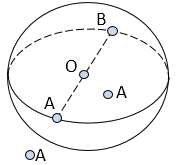
- Nếu OA = R ⇔ A ∈ S(O; R). Khi đó OA gọi là bán kính mặt cầu. Nếu OA và OB là hai bán kính sao cho \vec{OA}=-\vec{OB} thì đoạn thẳng AB gọi là một đường kính của mặt cầu.
- Nếu OA < R ⇔ A nằm trong mặt cầu.
- Nếu OA > R ⇔ A nằm ngoài mặt cầu.
2.2 Vị trí tương đối đường thẳng so với mặt cầu
Cho mặt cầu S(O; R) và một đường thẳng Δ. Gọi H là hình chiếu của O trên đường thẳng Δ và d = OH là khoảng cách từ tâm O của mặt cầu đến đường thẳng Δ. Khi đó:
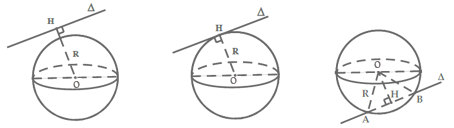
- Nếu d > R ⇔ Δ không cắt mặt cầu S(O; R).
- Nếu d < R ⇔ Δ cắt mặt cầu S(O; R) tại hai điểm phân biệt.
- Nếu d = R ⇔ Δ và mặt cầu tiếp xúc nhau (tại một điểm duy nhất). Do đó: điều kiện cần và đủ để đường thẳng Δ tiếp xúc với mặt cầu là d = d(O, Δ) = R.
Định lí: Nếu điểm A nằm ngoài mặt cầu S(O; R) thì:
- Qua có vô số tiếp tuyến với mặt cầu S(O; R).
- Độ dài đoạn thẳng nối A với các tiếp điểm đều bằng nhau.
- Tập hợp các điểm này là một đường tròn nằm trên mặt cầu S(O; R).
2.3 Vị trí tương đối mặt phẳng so với mặt cầu
Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P), gọi H là hình chiếu của O trên (P).
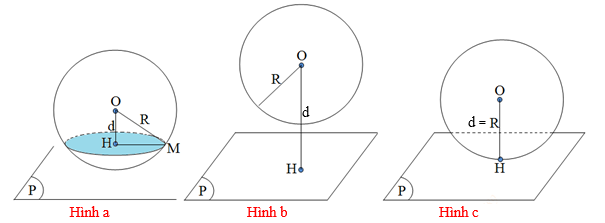
- Nếu OH<R thì (S) cắt (P) theo đường tròn tâm H và bán kính r=HM=\sqrt{R^2-OH^2} (Hình a).
- Nếu OH>R thì (S) và (P)không có điểm chung (Hình b).
- Nếu OH=R thì (S) tiếp xúc (P) tại tiếp điểm H (Hình c).
Đặc biệt: Nếu OH=0(O≡H) thì đường tròn giao tuyến của (P) và (S) được gọi là đường tròn lớn, (P) được gọi là mặt phẳng kính.
3. Mặt cầu ngoại tiếp khối chóp
3.1 Các khái niệm cần nắm
Trục của đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
Đường trung trực của đoạn thẳng: là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
Mặt trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.
3.2 Tâm và bán kính mặt cầu ngoại tiếp hình chóp
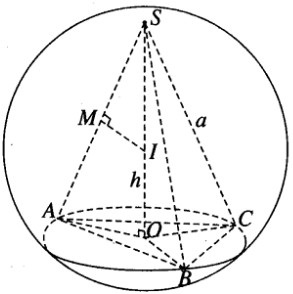
Tâm mặt cầu ngoại tiếp hình chóp: là điểm cách đều các đỉnh của hình chóp. Hay nói cách khác, nó chính là giao điểm I của trục đường tròn ngoại tiếp mặt phẳng đáy và mặt phẳng trung trực của một cạnh bên hình chóp.
Bán kính: là khoảng cách từ I đến các đỉnh của hình chóp.
4. Các dạng bài về khối cầu
- Tính thể tích, diện tích xung quanh của khối cầu
- Dạng bài khối cầu ngoại tiếp khối lăng trụ
- Dạng bài khối cầu ngoại tiếp khối chóp
- Dạng bài khối cầu ngoại tiếp khối nón
- Dạng bài khối cầu ngoại tiếp khối trụ tròn xoay
- Bài toán khối cầu nâng cao (liên quan đến thực tế, cực trị,..)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết về mặt cầu – mặt cầu ngoại tiếp khối chóp. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Mặt cầu
- 20 câu trắc nghiệm tính diện tích và thể tích mặt cầu có lời giải chi tiết
- Dạng toán xác định mặt cầu – hướng dẫn giải và bài tập
- Dạng toán mặt cầu ngoại tiếp nội tiếp lăng trụ – hướng dẫn giải và bài tập
- Phương pháp giải mặt cầu ngoại tiếp – nội tiếp hình chóp chi tiết nhất
- Vị trí tương đối của đường thẳng và mặt phẳng với mặt cầu trong không gian Oxyz





