Phương pháp giải hình nón ngoại tiếp nội tiếp hình chóp chi tiết nhất
Xin chào các bạn, hôm nay HocThatGioi sẽ trình bày đến các bạn phương pháp giải hình nón ngoại tiếp nội tiếp hình chóp và một số ví dụ bài tập có lời giải chi tiết để giúp các bạn nắm vững kiến thức hơn. Hãy cùng HocThatGioi theo dõi hết bài viết hôm nay nhé.
1. Phương pháp giải hình nón ngoại tiếp hình chóp
Hình nón ngoại tiếp hình chóp (hình chóp nội tiếp hình nón) thì đỉnh của hình chóp trùng với đỉnh của hình nón và đáy của hình nón là hình tròn ngoại tiếp đáy của hình chóp.
Sau đây là một số trường hợp chúng ta hay gặp trong các đề thi.
1.1 Hình nón ngoại tiếp hình chóp tam giác
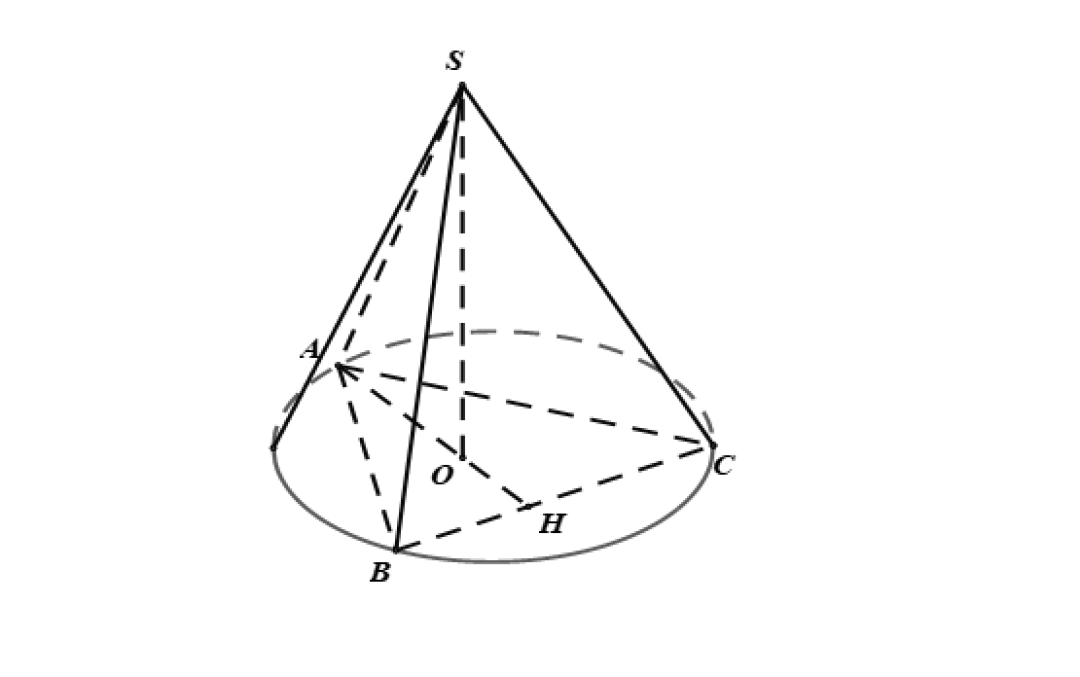
Gọi h_{nón}, r, l, h_{chóp} lần lượt là chiều cao, bán kính, đường sinh của hình nón và chiều cao hình chóp, ta có:
- h_{nón} = h_{chóp} = SO
- Tâm của đường đáy hình nón là tâm của đường tròn ngoại tiếp \Delta ABC là O
- Bán kính của hình nón r = OA = OB = OC.
- Đường sinh của hình nón l = SA = SB = SC
Ví dụ minh hoạ:
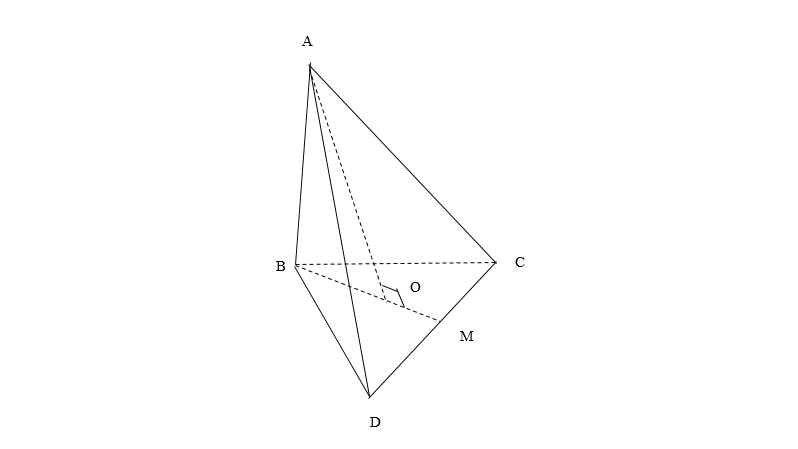
Dễ thấy, bán kính đường tròn ngoại tiếp \Delta BCD là OB = \frac{a\sqrt{3}}{3}.
Suy ra bán kính đáy hình nón là R = \frac{a\sqrt{3}}{3}.
Tam giác ABO vuông tại O, có AO = \sqrt{AB^{2} – OB^{2}} = \frac{a\sqrt{6}}{3}.
Do đó chiều cao của hình nón là h = AO = \frac{a\sqrt{6}}{3}
1.2 Hính nón ngoại tiếp hính chóp tứ giác
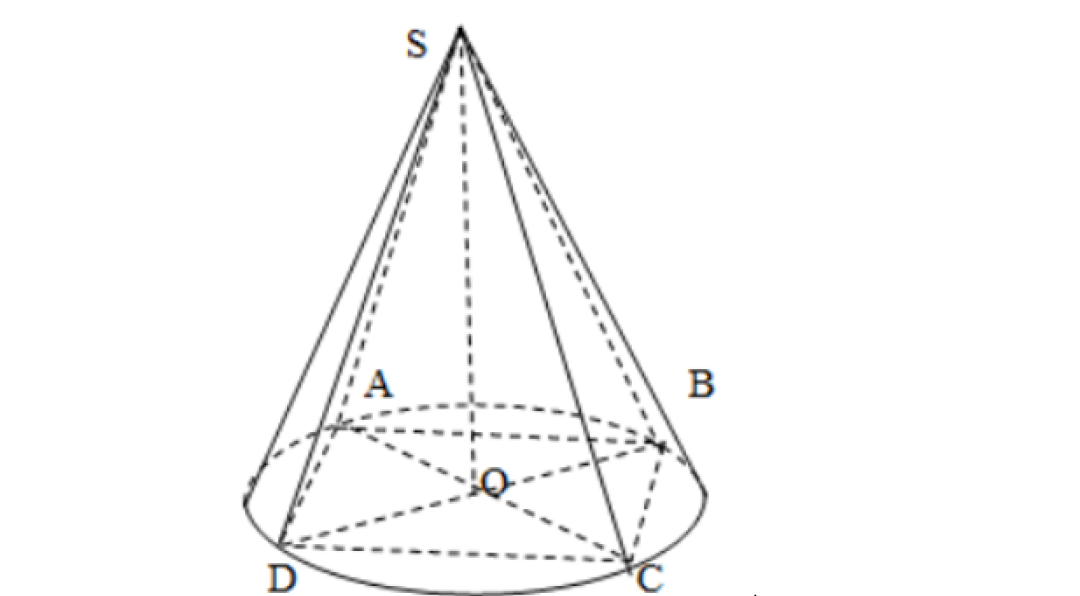
Gọi h_{nón}, r, l, h_{chóp} lần lượt là chiều cao, bán kính, đường sinh của hình nón và chiều cao hình chóp, ta có:
- h_{nón} = h_{chóp} = SO
- Tâm của đáy đường tròn đáy hình nón là tâm đường tròn ngoại tiếp tứ giác ABCD là O
- Bán kính của hình nón r = OA = OB = OC = OD
- Đường sinh của hình nón l = SA = SB = SC = SD
Ví dụ minh hoạ:
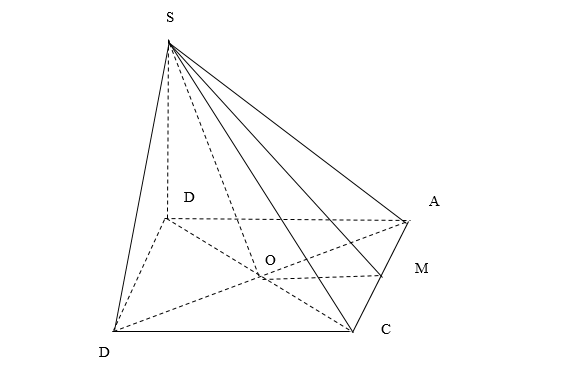
Mà S_{\Delta SAB} = 2a^{2} => SM = 4a.
Ta có \Delta SMO vuông tại M, có SO = \sqrt{SM^{2} – OM^{2}} = \frac{3\sqrt{7} a}{2}.
Bán kính đáy hình nón R = OB = \frac{DB}{2} = \frac{\sqrt{a^{2} + a^{2}}}{2} = \frac{a\sqrt{2}}{2}
Vậy V = \frac{1}{3}\pi R^{2}.h = \frac{a\sqrt{7}}{4}
2. Phương pháp giải hình nón nội tiếp hình chóp
Hình nón nội tiếp hình chóp (hình chóp ngoại tiếp hính nón) thì đỉnh của hình chóp trùng với điểm của hình nón và đáy của hình nón là hình tròn nội tiếp đáy của hình chóp
Sau đây là một số trường hợp chúng ta hay gặp trong các đề thi.
2.1 Hình nón nội tiếp hình chóp tam giác
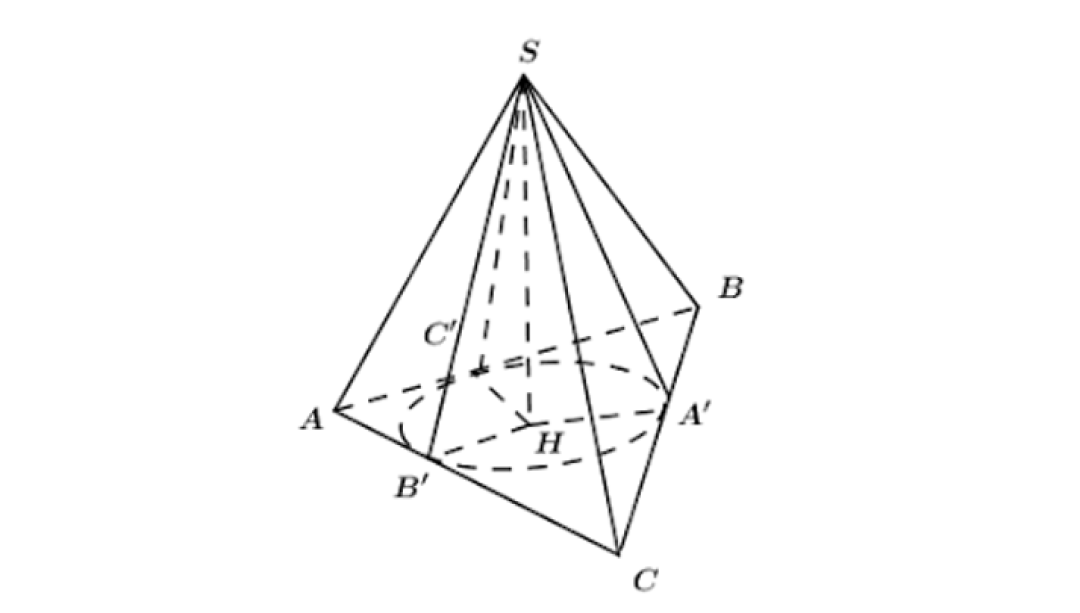
Gọi h_{nón}, r, l, h_{chóp} lần lượt là chiều cao, bán kính, đường sinh của hình nón và chiều cao hình chóp, ta có:
- h_{nón} = h_{chóp} = SH
- Tâm của đáy đường tròn đáy hình nón là tâm đường tròn nội tiếp tam giác ABD là H
- Bán kính của hình nón r = OA' = OB' = OC'
- Đường sinh của hình nón l = SA' = SB' = SC'
Ví dụ minh hoạ:
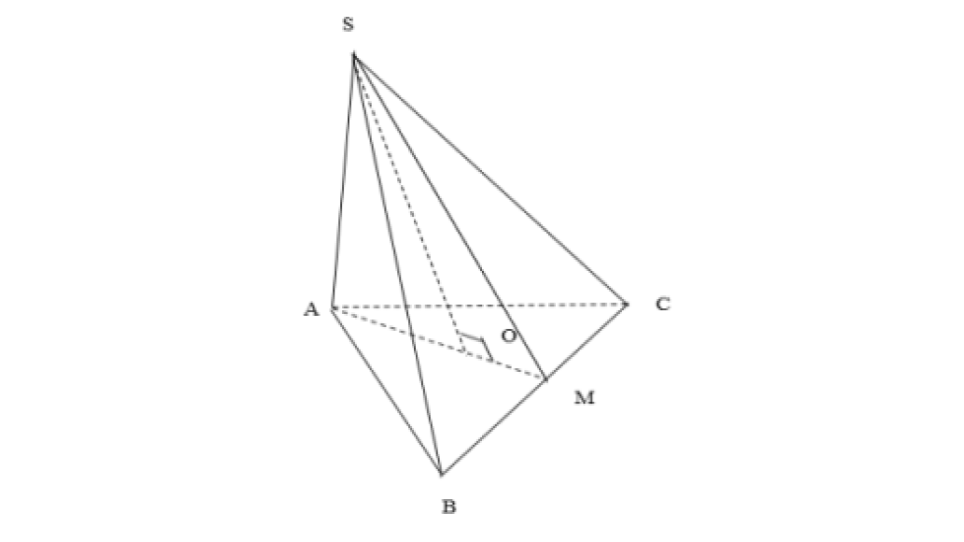
Dễ thấy, bán kính đường tròn đáy nội tiếp R = OM = \frac{a\sqrt{3}}{6}.
Tam giác SAO vuông tại O, có SO = \sqrt{SA^{2} – OA^{2}} = \frac{a\sqrt{6}}{3}.
Vậy V = \frac{1}{3}\pi R^{2}h = \frac{\sqrt{6}\pi a^{3}}{108}
2.2 Hình chóp nội tiếp hình chóp tứ giác
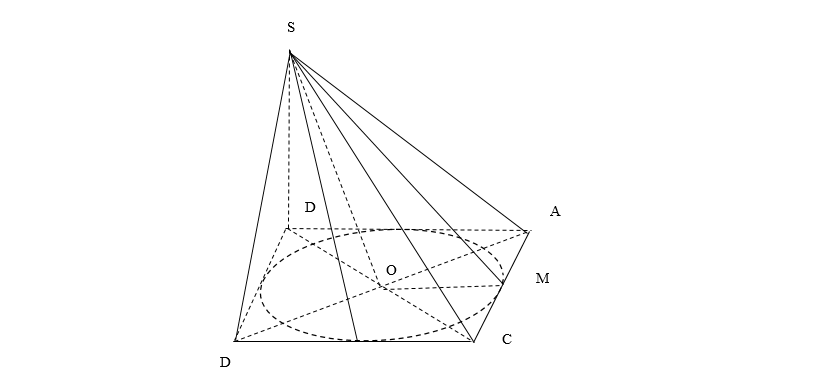
Hình nón có : Tâm O, bán kính r = OM, chiều cao h = SO, đường sinh l = SM
Ví dụ minh hoạ:
Đường sinh của hình nón : l = SM = \sqrt{SC^{2} – MC^{2}} = \sqrt{((4a)^{2} – \frac{a^{2}}{4}} = \frac{3\sqrt{7}}{2}
Vậy S_{xq} = \pi Rl = \frac{3\sqrt{7}}{4}\pi
(Xem hình nón nội tiếp hình chóp tứ giác)
Trên đây là bài viết Phương pháp giải hình nón ngoại tiếp nội tiếp hình chóp chi tiết nhất mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương Mặt tròn xoay để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt.
Bài viết khác liên quan đến Lớp 12 – Toán – Khái niệm mặt tròn xoay
- Lý thuyết mặt nón và mặt trụ hay đầy đủ nhất
- Lý thuyết Hình nón cụt và bài tập chi tiết dễ hiểu nhất
- 20 câu trắc nghiệm bài tập Hình nón dễ hiểu có lời giải chi tiết
- Tổng hợp các câu trắc nghiệm Hình nón vận dụng – vận dụng cao có lời giải
- 20 câu trắc nghiệm bài tập Hình trụ dễ hiểu có lời giải chi tiết nhất
- Tương giao giữa hình trụ và mặt phẳng, đường phẳng
- Dạng toán sự tạo thành mặt trụ, hình trụ – hướng dẫn giải và bài tập
- Dạng toán sự tạo thành mặt nón, hình nón – hướng dẫn giải và bài tập
- Lý thuyết mặt tròn xoay – mặt nón và mặt trụ chi tiết nhất
- Dạng toán tương giao giữa hình nón và mặt phẳng – hướng dẫn giải và bài tập
- Dạng toán mặt cầu ngoại tiếp nội tiếp lăng trụ – hướng dẫn giải và bài tập
- Tổng hợp bài tập hình nón ngoại tiếp nội tiếp có lời giải chi tiết nhất
- Tổng hợp các câu bài tập mặt cầu nội tiếp ngoại tiếp có lời giải chi tiết nhất
- Phương pháp giải hình nón ngoại tiếp nội tiếp hình trụ chi tiết nhất





