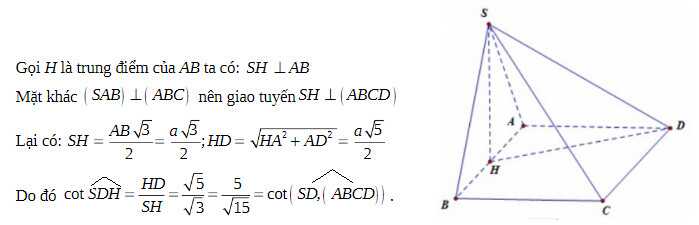
Góc giữa đường thẳng và mặt phẳng cực chi tiết và dễ hiểu.

Xin chào các bạn, trong bài viết hôm nay HocThatGioi sẽ giúp bạn ghi nhớ một cách dễ dàng nhất cách xác định góc giữa một đường thẳng và mặt phẳng. Hãy cùng HocThatGioi chinh phục hình học không gian bằng cách theo dõi hết bài viết bên dưới nhé!

1. Định nghĩa góc giữa đường thẳng và mặt phẳng

Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) là 90^0

Nếu a \bot (P) \Rightarrow \widehat{ (a,(P)) } = 90^0

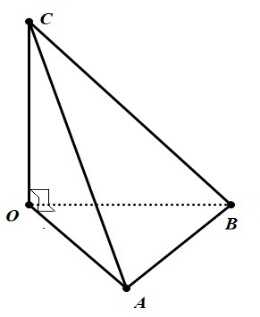
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì ta nói góc giữa đường thẳng a và hình chiếu của nó a ' lên mặt phẳng (P) gọi là góc giữa đường thẳng a và mặt phẳng (P)

Nếu a \not \perp (P) \Rightarrow \widehat{ (a,(P)) } = \widehat{ (a,a')} , với a ' là hình chiếu của a lên mặt phẳng (P)

2. Cách xác định góc giữa đường thẳng và mặt phẳng

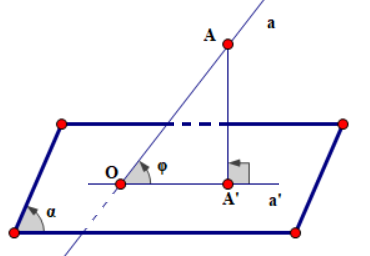
Vậy để tính góc của đường thẳng và mặt phẳng ta cần tìm được hình chiếu của đường thẳng lên phẳng đó theo các bước sau:

Bước 1: Tìm giao điểm O giữa đường thẳng a và mặt phẳng (\alpha) .

Bước 2: Từ một điểm A bất kì trên đường thẳng a kẻ đường vuông góc xuống mặt phẳng (\alpha) .

Bước 3: Góc \varphi= \widehat{AOA'} là góc cần tìm.

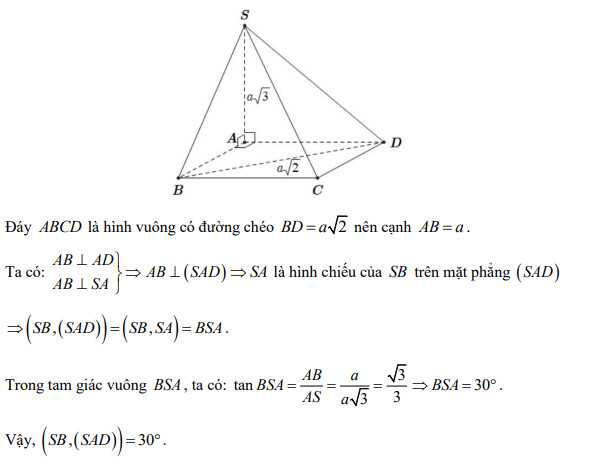
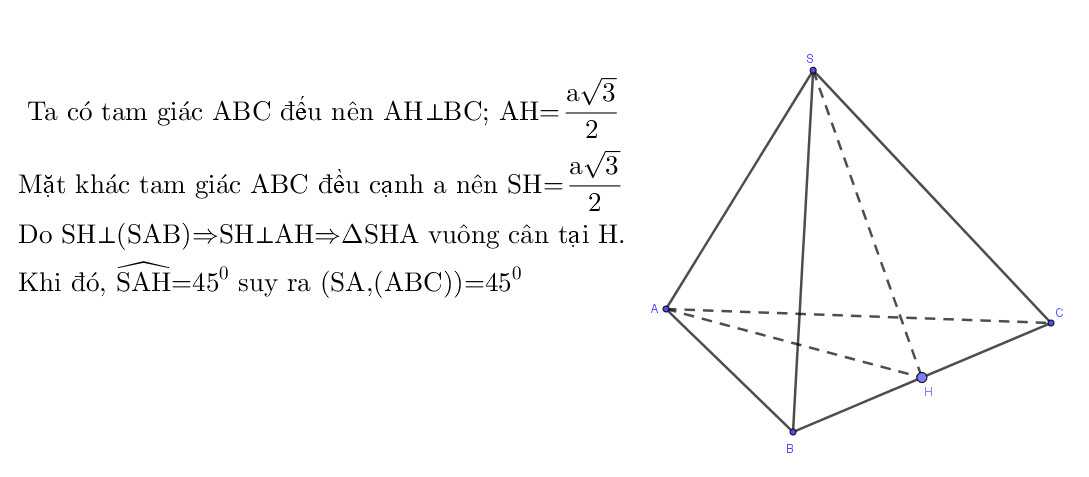
3. Bài tập vận dụng góc giữa đường thẳng và mặt phẳng

Ví dụ 1: Cho tứ diện OABC có OA,OB,OC vuông góc với nhau từng đôi một. Xác định góc giữa cạnh BC và mặt phẳng (OAB) .

• a. \widehat{CBA}
• b. \widehat{ABO}
• c. \widehat{BCO}
• d. \widehat{BCA}

Xem bài giải

Ta có OA,OB,OC vuông góc với nhau từng đôi một.
Suy ra: \begin{cases} OB \bot OA \\ OB \bot OC \end{cases} \Rightarrow OB \bot (OAC)
Ta có C là điểm chung giữa mặt phẳng (OAC) và cạnh BC, O là hình chiếu của B xuống mặt phẳng (OAC).
Nên góc giữa cạnh BC và mặt phẳng (OAB) là \widehat{BCO} .

Ví dụ 2: Cho hình chóp S.ABCD có SD vuông góc với mặt phẳng đáy. Tứ giác ABCD là hình chữ nhật. Góc giữa đường thẳng SC và mặt phẳng (SAD) là

• a. \widehat{BAC}
• b. \widehat{SCD}
• c. \widehat{SCB}
• d. \widehat{CSD}

Xem bài giải

Ta có: \begin{cases} CD \bot AD \\ CD \bot SD \end{cases} \Rightarrow CD \bot (SAD)
Suy ra CD là hình chiếu của SC xuống mặt phẳng (SAD).
Suy ra: \widehat{(SC,(SAD))}= \widehat{(SC,SD)}=\widehat{CSD} .

Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình vuông và SA vuông góc với mặt phẳng đáy và SA=a\sqrt{3}, BD= a\sqrt{2} . Góc giữa đường thẳng SB và mặt phẳng (SAD) bằng

• a. 30^0
• b. 45^0
• c. 60^0
• d. 90^0

Xem bài giải

Ví dụ 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều. Góc giữa đường thẳng SA và mặt phẳng (SAD) bằng

• a. 60^0
• b. 30^0
• c. 45^0
• d. 75^0

Xem bài giải

Ví dụ 5: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác (SAB) đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Tính cot góc giữa đường thẳng SB và mặt phẳng (SAD) là

• a. \frac{\mathrm{ \sqrt{5} } }{\mathrm{ 15}}
• b. \frac{\mathrm{ \sqrt{3} } }{\mathrm{ 2}}
• c. \sqrt{3}
• d. \frac{\mathrm{ 5 } }{\mathrm{ \sqrt{15}}}

Xem bài giải

Cảm ơn các bạn đã xem hết bài học hôm nay, HocThatGioi hi vong bài học hôm nay sẽ giúp các bạn tự tin hơn khi gặp những dạng bài này. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi nhá. Đừng quên để lại 1 like, 1 cmt để tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!

Bài viết khác liên quan đến Lớp 12 – Toán – Phương trình đường thẳng trong không gian

• Phương trình đường thẳng, mặt phẳng và mặt cầu trong không gian Oxyz hay chi tiết nhất
• Phương trình đường thẳng trong không gian Oxyz – Góc và khoảng cách giữa đường thẳng
• Cách tính khoảng cách giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
• Cách viết phương trình đường thẳng trong không gian Oxyz – bài tập áp dụng
• Hình chiếu vuông góc của điểm lên đường thẳng lên mặt phẳng trong không gian Oxyz
• Quan hệ vuông góc và song song của đường thẳng, mặt phẳng trong không gian
• Vị trí tương đối của đường thẳng và mặt phẳng trong không gian siêu chi tiết.
• Cách tính khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian Oxyz-bài tập áp dụng
• Cách tính góc giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
• Cách tính góc giữa đường thẳng và mặt phẳng trong không gian Oxyz – bài tập áp dụng
• Vị trí tương đối của đường thẳng và mặt phẳng với mặt cầu trong không gian Oxyz
• Vị trí tương đối của hai đường thẳng trong không gian siêu dễ.