Vị trí tương đối của đường thẳng và mặt phẳng trong không gian siêu chi tiết.
Trong bài này, HocThatGioi sẽ giới thiệu cho các bạn về Các vị trí tương đối của đường thẳng với mặt phẳng từ đó xây dựng lý thuyết đường thẳng song song với mặt phẳng, bài viết sẽ giúp các bạn biết được các vị trí tương đối giữa đường thẳng và mặt phẳng, cũng như cách để chứng minh đường thẳng song song với mặt phẳng một cách đơn giản và dễ hiểu nhất nhé!
1. Vị trí tương đối của đường thẳng và mặt phẳng.
Cho đường thẳng d và mặt phẳng (\alpha) , ta có ba vị trí tương đối giữa chúng là:
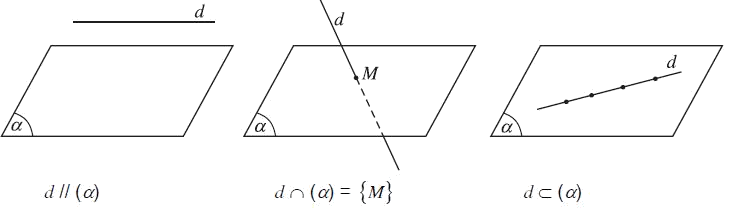
- d song song với (\alpha)[ , kí hiệu d// (\alpha) hoặc (\alpha)//d. (hình 1)
- d và (\alpha) cắt nhau tại M kí hiệu M=d \cap (\alpha) . ( hình 2)
- d nằm trong (\alpha) , kí hiệu d \subset (\alpha) . (hình 3)
2. Các định lý và tính chất đường thẳng song song với mặt phẳng
Định lý 1:
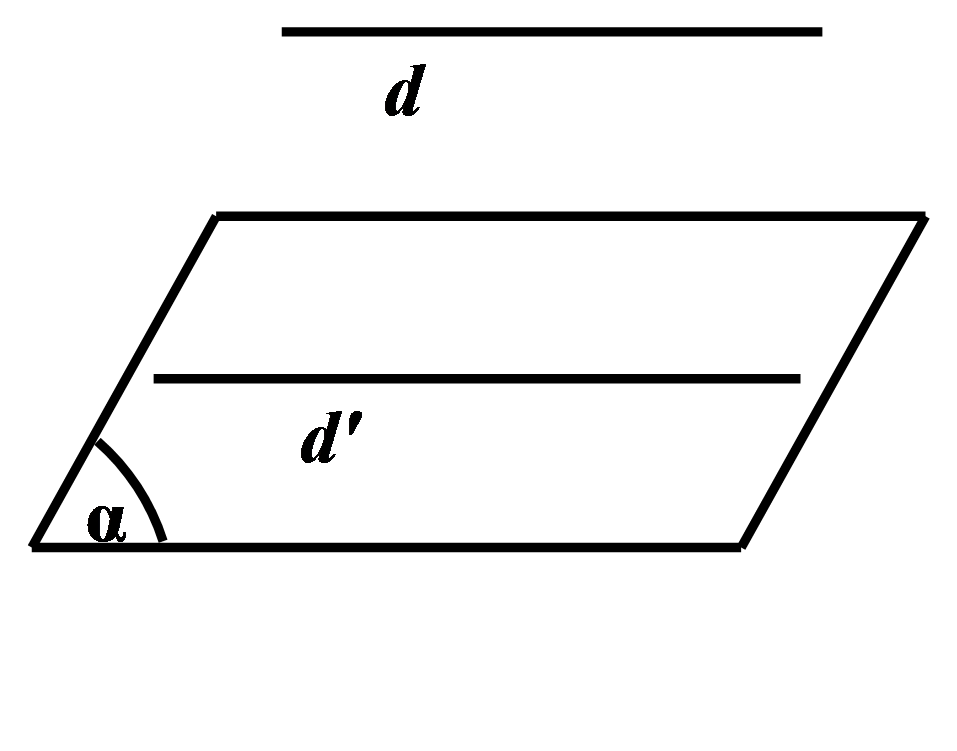
Nếu đường thẳng d không nằm trong mặt phẳng (\alpha) và d song song với đường thẳng d' nằm trong (\alpha) thì d song song với (\alpha) .
Vậy \left\{\begin{matrix} d \nsubseteq (\alpha)\\ d'//d \\ d'\subseteq (\alpha ) \end{matrix}\right. \Rightarrow d //(\alpha) .
Định lí 2
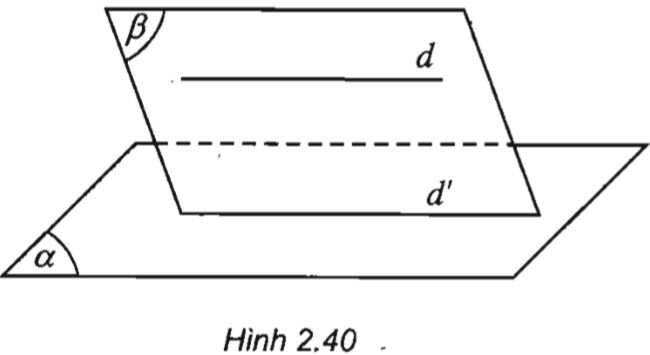
Cho đường thẳng d song song với mặt phẳng (\alpha) . Nếu mặt phẳng (\beta) đi qua d và cắt (\alpha) theo giao tuyến d' thì d//d'
Vậy \left\{\begin{matrix} d// (\alpha)\\ d\subset (\beta )\\ (\alpha )\cap (\beta ) \end{matrix}\right. \Rightarrow d'//d
Định lí 3
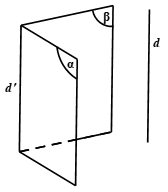
Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng ( nếu có) cũng song song với đường thẳng đó.
Vậy \left\{\begin{matrix} (\alpha)// d \\ (\beta )// d \\ (\alpha )\cap (\beta )=d' \end{matrix}\right. \Rightarrow d //d'
Hệ quả
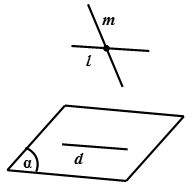
Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
3. Các định lý và tính chất của đường thẳng vuông góc với mặt phẳng.
Định lý
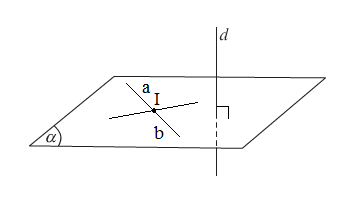
d vuông góc với mặt phẳng (\alpha) nếu d vuông góc với hai đường thẳng cắt nhau cùng nằm trong (\alpha)
\left\{\begin{matrix} d \bot a \\ d \bot b \\ a, b \subset (\alpha) , a \cap b=I \end{matrix}\right. \Rightarrow d \bot (\alpha)Tính chất 1
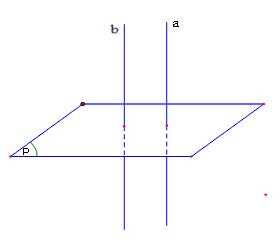
Nếu hai đường thẳng cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
Ta có: \left\{\begin{matrix} a \neq b \\ a \bot (P) , b \bot (P) \end{matrix}\right. \Rightarrow a//b
Ngược lại nếu một mặt phẳng vuông góc với một trong hai đường thẳng song song thì nó sẽ vuông góc với đường thẳng còn lại.
Ta có: \left\{\begin{matrix} a \\ b // a \bot (P) \end{matrix}\right. \Rightarrow b \bot (P)
Tính chất 2
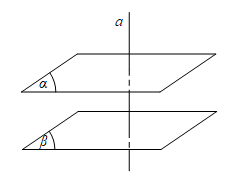
Nếu một đường thẳng vuông góc với một trong hai mặt phẳng song song thì nó vuông góc với mặt phẳng còn lại.
Ta có: \left\{\begin{matrix} (\alpha) // (\beta) \\ a \bot (\alpha) \end{matrix}\right. \Rightarrow a// (\beta)
Nếu một đường thẳng cùng vuông góc với hai mặt phẳng phân biệt thì hai mặt phẳng đó song song với nhau.
Ta có: [ Ta có: \left\{\begin{matrix} (\alpha) \neq (\beta) \\ a \bot (\alpha) , a \bot (\beta) \end{matrix}\right. \Rightarrow (\alpha) // (\beta)
Tính chất 3
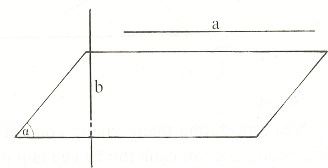
Nếu một đường thẳng song song với mặt phẳng thì chúng sẽ cùng vuông góc với một đường thẳng.
Ta có: \left\{\begin{matrix} a// (\alpha) \\ b \bot (\alpha) \end{matrix}\right. \Rightarrow b \bot a
Ngược lại nếu một đường và một mặt phẳng (không hcuwas đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
Ta có: \left\{\begin{matrix} a \nsubseteq (\alpha) \\ a \bot b, b \bot (\alpha) \end{matrix}\right. \Rightarrow a // (\alpha)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Nắm trọn kiến thức cơ bản về các vị trí tương đối của đường thẳng và mặt phẳng trong không gian. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực hay góp ý cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Phương trình đường thẳng trong không gian
- Phương trình đường thẳng, mặt phẳng và mặt cầu trong không gian Oxyz hay chi tiết nhất
- Phương trình đường thẳng trong không gian Oxyz – Góc và khoảng cách giữa đường thẳng
- Cách tính khoảng cách giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
- Cách viết phương trình đường thẳng trong không gian Oxyz – bài tập áp dụng
- Hình chiếu vuông góc của điểm lên đường thẳng lên mặt phẳng trong không gian Oxyz
- Quan hệ vuông góc và song song của đường thẳng, mặt phẳng trong không gian
- Góc giữa đường thẳng và mặt phẳng cực chi tiết và dễ hiểu.
- Cách tính khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian Oxyz-bài tập áp dụng
- Cách tính góc giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
- Cách tính góc giữa đường thẳng và mặt phẳng trong không gian Oxyz – bài tập áp dụng
- Vị trí tương đối của đường thẳng và mặt phẳng với mặt cầu trong không gian Oxyz
- Vị trí tương đối của hai đường thẳng trong không gian siêu dễ.





