Khảo sát sự biến thiên và vẽ đồ thị chương hàm số cực đầy đủ và chi tiết
Bài viết này, HocThatGioi sẽ hướng dẫn các bạn các bước khảo sát sự biến thiên và vẽ đồ thị của hàm số cơ bản hay gặp nhất, giúp các bạn có thể dễ dàng nhận dạng được các loại đồ thị khác nhau, nếu các bạn còn đang gặp vấn đề về dạng bài đồ thị này thì còn chần chừ gì nữa mà không cùng HocThatGioi bắt đầu bài học ngay bây giờ nào.
1. Khảo sát đồ thị hàm số
Bước 1: Tìm tập xác định của hàm số
Bước 2: Đạo hàm tìm nghiệm của y'=0 hoặc các điểm làm hàm số không xác định
Bước 3: Xét dấu, vẽ bảng biến thiên
Bước 4: Vẽ đồ thị
Để hiểu rõ hơn về phương pháp làm, chúng ta cùng nhau đi đến ví dụ minh họa cụ thể trong các phần sau để nắm rõ hơn nhé.
2. Đồ thị hàm số chương hàm số
2.1 Đồ thị hàm số bậc 3
Cho hàm số y=ax^3+bx^2+cx+d (a\neq 0). Khi đó ta khảo sát đồ thị như sau:
Bước 1: Tập xác định D=\mathbb{R}
Bước 2: Tìm đạo hàm: y'=3ax^2+2bx+c
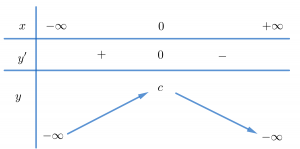
Bước 3: Vẽ bảng biến thiên
Xét \Delta '=b^2-3ac
TH1: Nếu \Delta '>0 thì phương trình y'=0 có 2 nghiệm phân biệt.
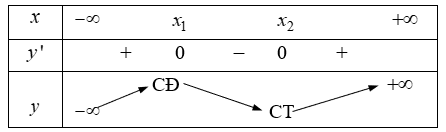
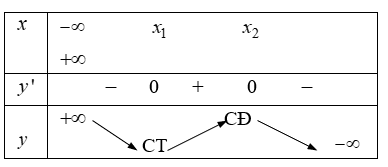
TH2: Nếu \Delta ' \leqslant 0 thì phương trình y'=0 có nghiệm kép, do đó qua nghiệm này y' không đổi dấu
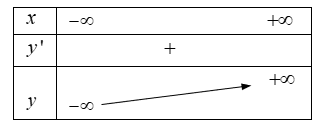
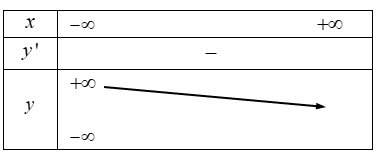
Bước 4: Vẽ đồ thị
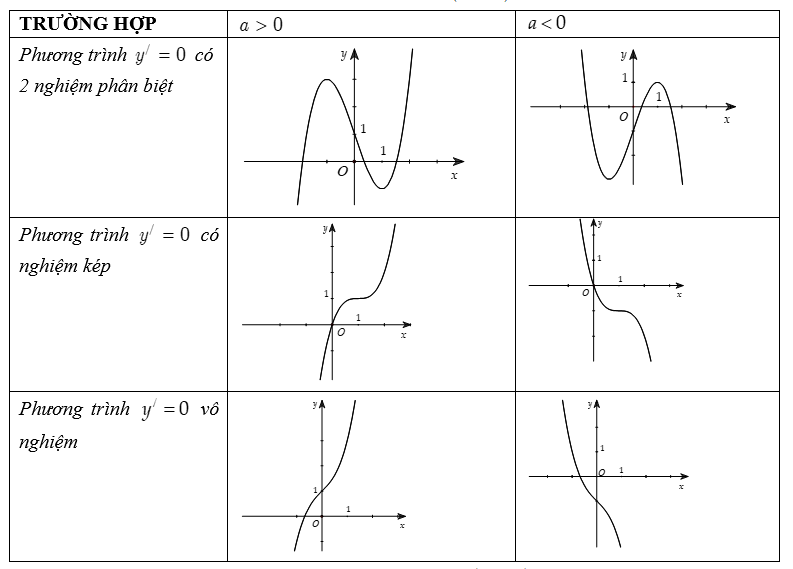
2.2 Đồ thị hàm số trùng phương
Cho hàm số y=ax^4+bx^2+c (a\neq 0) , khi đó ta khảo sát đồ thị hàm số như sau
Bước 1: Tập xác định D=\mathbb{R}
Bước 2: Tìm nghiệm đạo hàm: y'=4ax^3+2bx=0
Suy ra: x=0 hoặc x^2=-\frac{b}{2a}
Bước 3: Vẽ bảng biến thiên
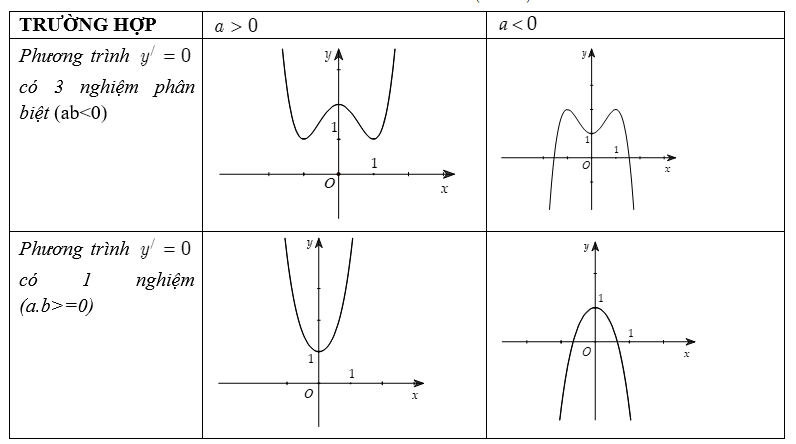
TH1: Nếu a.b < 0 thì phương trình y'=0 có 3 nghiệm phân biệt.
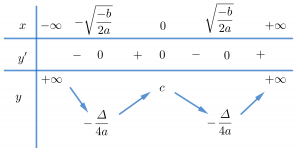
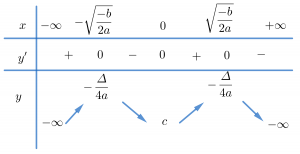
TH2: Nếu \Delta ' \geq 0 thì phương trình y'=0 1 nghiệm đơn mà qua đó làm y' đổi dấu
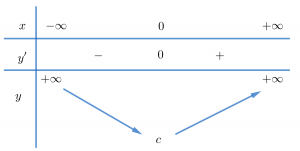
Bước 4: Vẽ đồ thị
2.3 Đồ thị hàm số phân thức
Cho hàm số y=\frac{ax+b}{cx+d}, khi đó ta khảo sát hàm số như sau
Bước 1: Tập xác định D=\mathbb{R} \setminus \left\{ \frac{-d}{c}\right\}
Bước 2: Đạo hàm y=\frac{ad\:-\:bc}{(cx+d)^2}
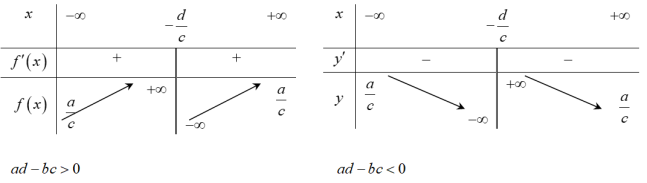
Bước 3: Khảo sát sự biến thiên
Đồ thị hàm số nhận y=\frac{a}{c} làm tiệm cận ngang và x=\frac{-d}{c} làm tiệm cận đứng.
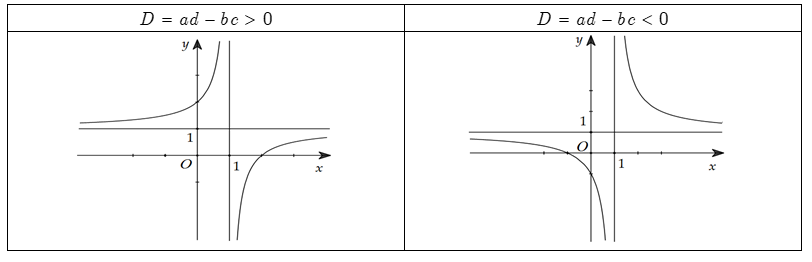
TH1: ad\:-\:bc > 0, khi đó hàm số đồng biến trên từng khoảng xác định
TH2: ad\:-\:bc < 0, khi đó hàm số nghịch biến trên từng khoảng xác định
Bước 4: Vẽ đồ thị
Trên đây là Lý thuyết khảo sát đồ thị chương hàm số. Trong các bài viết tiếp theo, chúng ta sẽ cùng nhau đi chinh phục các dạng bài tập khảo sát hàm số nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hi vọng rằng bài viết sẽ mang lại thêm các kiến thức bổ ích cho các bạn. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt!





