Lý thuyết phép vị tự đầy đủ nhất

Quang Thái Tháng Một 18, 2022

Xin chào các bạn, bài viết hôm nay sẽ đem đến cho các khái niệm, tính chất,.. của phép vị tự ngoài ra sẽ có một số bài tập biểu thức toạ độ. Nhằm giúp các bạn hệ thống hoá được kiến thức bài học. Hãy theo dõi hết bài viết cùng HocThatGioi nhé.

1. Định nghĩa

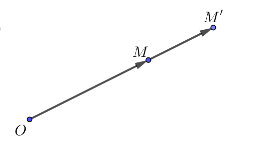
Cho điểm $O$ cố định và mốt số $k$ không đổi, $k \neq 0$ . Khi đó phép vị tự tâm $O$ tỷ số $k \neq 0$ là phép biến hình biến mỗi điểm $M$ thành $M'$ sao cho $\overrightarrow{OM'} = k\overrightarrow{OM}$

Ký hiệu phép vị tự

V_{(O;k)}(M) = M’ \Leftrightarrow \overrightarrow{OM’} = k\overrightarrow{OM}

Nhận xét:
– Phép vị tự biến tâm vị tự thành chính nó
– Khi

k > 0

thì

M

và

M’

cùng phía với điểm

O

– Khi

k = -1

thì

M

và

M’

đối xứng nhau qua điểm

O

– Khi

k = 0

thì

M

và

M’

có vị trí trùng nhau nên phép vị tự tỷ số k = 1 là phép đồng nhất
–

V_{(O;k)}(M) = M’ \Leftrightarrow V_{(O;\frac{1}{k})}(M’) = M

2. Tính chất

Lý thuyết phép vị tự đầy đủ nhất 6 — Tính chất 1

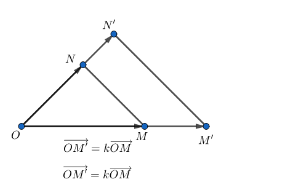
Tính chất 1: Nếu phép vị tự tỷ số $k$ biến ham điểm $M, N$ tuỳ ý thành hai điểm $M', N'$ thì $\overrightarrow{M'N'} = k\overrightarrow{MN}$ và $M;N' = |k|MN$

Lý thuyết phép vị tự đầy đủ nhất 7 — Tính chất 2

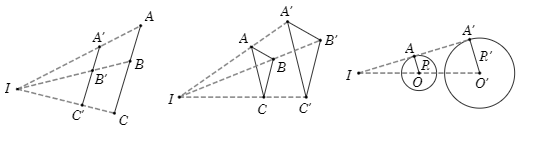
Tính chất 2: Phép vị tự tỷ số $k$ biến:

Ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa cácđiểm.
Đường thẳng thành đường thẳng song song hoặc trùng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Tam giác thành tam giác đồng dạng với nó, góc thành góc bằng nó.
Đường tròn bán kính R thành đường tròn có bán kính |k|R.

3. Cách tìm tâm vị tự của hai đường tròn

Cho hai đường trong $(I,R)$ và $(I';R')$

Trường hợp 1: Trường hợp $I$ trùng với $I'$

Lý thuyết phép vị tự đầy đủ nhất 8 — Trường hợp 1

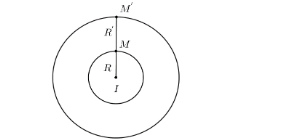
Phép vị tự tâm $I$ , tỉ số $\frac{R'}{R}$ và phép vị tự tâm $I$ , tỉ số $-\frac{R'}{R}$ biến đường tròn $(I,R)$ thành đường tròn $(I',R')$

Trường hợp 2: Trường hợp $I$ khác $I'$ và $R \neq R'$

Lý thuyết phép vị tự đầy đủ nhất 9 — Trường hợp 2

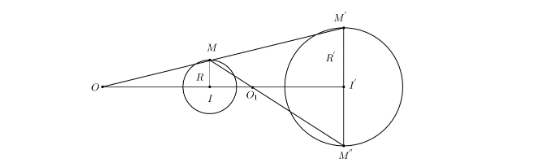
Lấy $M'$ bất kì thuộc $(I;R)$ , đường thẳng qua $I'$ song song với $IM$ cắt $(I';R')$ tại $M'$ và $M''$

Giả sử $M, M'$ nằm cung phía đối với đường thẳng $II'$ , còn $M, M''$ nằm khác phía với đường thẳng $II'$

Giả sử đường thẳng $MM'$ cắt $II'$ tại $O$ nằm ngoài đường thẳng $II'$ , còn đường thẳng $MM'$ cắt $II'$ tại $O_{1}$ nằm ngoài đoạn thẳng $II'$ .

Khi đó phép vị tự tâm $O$ tỉ số $\frac{R'}{R}$ và phép vị tự tâm $O_{1}$ , tỉ số $-\frac{R'}{R}$ biến đường tròn $(I,R)$ thành đường tròn $(I',R')$

Ta gọi $O$ là tâm vị tự ngoài, còn $O_{1}$ là tâm vị tự tròn của $2$ đường tròn.

Trường hợp 3: Trường hợp $I$ khác $I'$ và $R = R'$ .

Lý thuyết phép vị tự đầy đủ nhất 10 — Trường hợp 3

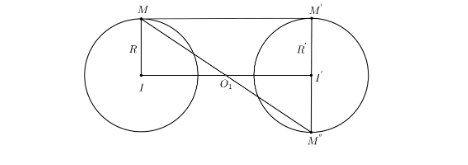
Khi đó $MM'$ song song với $II'$ nên chỉ có phép vị tự tâm $O_{1}$ , tỉ số $k = -\frac{R'}{R} = -1$ biến đường tròn $(I;R)$ thành đường tròn $(I';R')$

Nó chính là phép đối xứng tâm $O_{1}$

4. Biểu thức toạ độ

Trong mặt phẳng $Oxy$ , cho điểm $M(x;y)$ và điểm $M'$ là ảnh của $M$ qua phép quay vị tự tâm $I$ . Khi đó:

Biểu thức toạ độ

V_{(I;k)}(M) = M’ \Leftrightarrow \overrightarrow{IM’} = k\overrightarrow{IM} \Leftrightarrow (x – a’;y’ – b) = k(x – a;y – b) \Leftrightarrow \left\{\begin{matrix}x’ – a = k(x – a)\\y’ – b = k(y – b)\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x’ = a + k(x – a)\\y’ = b + k(y – b)\end{matrix}\right.

Vi dụ 1: Trong mặt phẳng Oxy cho hai điểm M(4;6) và M'(-3;5). Phép vị tự tâm I, tỉ số

k = \frac{1}{2}

biến điểm M thành điểm M’. Tìm toạ độ vị tự I.

Gọi

I(x;y)

. Suy ra

\overrightarrow{IM} = (4 – x;6 – y), \overrightarrow{IM’} = (-3 – x; 5 – y)

Ta có

V_{(I;\frac{1}{2})}M = M’ \Leftrightarrow \overrightarrow{IM’} = \frac{1}{2}\overrightarrow{IM} \Leftrightarrow \left\{\begin{matrix}-3 – x = \frac{1}{2}(4 – x)\\5 – y = \frac{1}{2}(6 – y)\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -10\\ y = 4\end{matrix}\right. \Rightarrow I(-10;4)

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết phép vị tự đầy đủ nhất. Nếu thấy bài viết hay, bổ ích hãy chia sẻ ngay cho bạn bè của mình để cùng nhau học giỏi nhé! Chúc các bạn học tốt!