Lý thuyết mặt tròn xoay – mặt nón và mặt trụ chi tiết nhất

Quang Thái Tháng Mười Một 23, 2021

Xin chào các bạn, hôm nay HocThatGioi sẽ đem đến cho các bạn một khái niệm mới, đó là mặt tròn xoay. Đồng thời các bạn sẽ cùng HocThatGioi đi tìm hiểu kĩ hai mặt tròn xoay phổ biết là mặt nón và mặt trụ cũng như các khái niệm hình nón, hình trụ, khối nón và khối trụ. Hãy cùng với HocThatGioi bắt đầu buổi học hôm nay nhé.

1. Sự tạo thành mặt tròn xoay

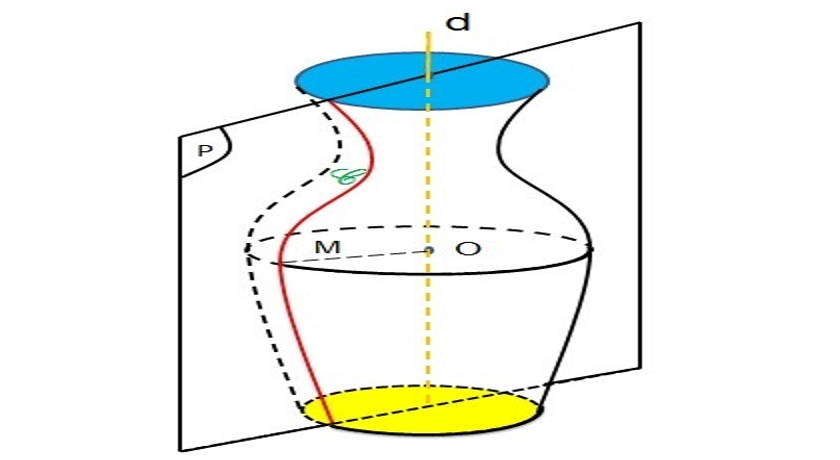
Trong không gian cho mặt phẳng $(P)$ chứa đường thẳng $d$ và một đường $\varepsilon$ . Khi quay mặt phẳng $(P)$ quanh $d$ một góc $360^{\circ}$ thì mỗi điểm $M$ trên đường thẳng $\varepsilon$ vạch ra một đường tròn có tâm $O$ thuôc $d$ và nằm trên mặt phẳng vuông góc với $d$ . Như vậy khi quay mặt phẳng $(P)$ quanh đường thẳng $d$ thì đường $\varepsilon$ sẽ tạo nên một hình được gọi là là mặt tròn xoay.

Đường $\varepsilon$ được gọi là đường sinh của mặt tròn xoay.
Đường thẳng $d$ được gọi là trục của mặt tròn xoay.

2. Mặt nón tròn xoay

Sau đây là định nghĩa mặt nón, hình nón, khối nón tròn xoay.

2.1 Định nghĩa mặt nón tròn xoay

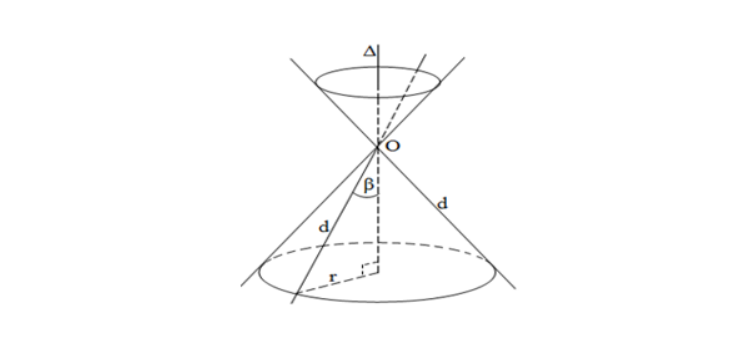
Trong mặt phẳng $(P)$ cho hai đường thẳng $d$ và $\Delta$ cắt nhau tại điểm $O$ và tạo thành góc β với $0^{\circ} < β < 90^{\circ}$ . Khi quay mặt phẳng $(P)$ xung quanh $\Delta$ thì đường thẳng $d$ sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh $O$ (gọi tắt là mặt nón).

Đường thẳng $\Delta$ gọi là trục.
Đường thẳng $d$ goi là đường sinh.
Góc $2β$ goi là góc ở đỉnh của mặt nón đó.

2.2 Hình nón tròn xoay và khối nón tròn xoay

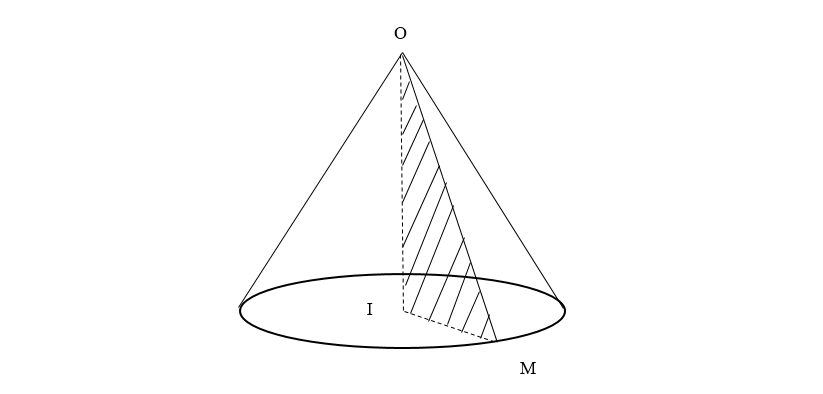
Cho tam giác $OIM$ vuông tai $I$ . Khi quay tam giác đó xung quanh cạnh góc vuông $OI$ thì đường gấp khúc $OMI$ tạo thành một hình được gọi là hình nón tròn xoay (gọi tắt là hình nón)

Hình tròn tâm $I$ sinh bởi các điểm thuộc canh $IM$ khi $IM$ quay quanh trục $OI$ được gọi là mặt đáy của hình nón . .
Điểm $O$ gọi là đỉnh của hình nón.
Độ dài $OI$ gọi là chiều cao của hình nón cũng là khoảng cách từ $O$ tới mặt phẳng đáy.
Độ dài đoạn $OM$ gọi là độ dài đường sinh của hình nón.
Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh $OM$ khi quay quanh trục $OI$ gọi là mặt xung quanh của hình nón.

Khối nón tròn xoay là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó. Người ta còn gọi tắt khối nón tròn xoay là khối nón.

Những điểm không thuộc khối nón được gọi là những điểm ngoài của khối nón.
Những điểm thuộc khối nón được gọi là những điểm trong của khối nón.
Ta gọi đỉnh, mặt đáy, đường sinh của một hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.

2.3. Công thức diện tích hình nón và thể tích khối nón

Cho hình nón có chiều cao là $h$ , bán kính đáy $r$ và đường sinh là $l$ thì có:

Diện tích xung quanh: $S_{xq}$ = $\pi rl$ .
Diện tích đáy: $S_{đ}$ = $\pi r^{2}$ .
Diện tích toàn phần $S_{tp}=S_{xq}+S_{đ}=\pi rl + \pi r^{2}$ .
Thể tích khối nón: $V = \frac{1}{3}\pi r^{2}h$ .

3. Mặt trụ tròn xoay

3.1 Định nghĩa mặt trụ tròn xoay

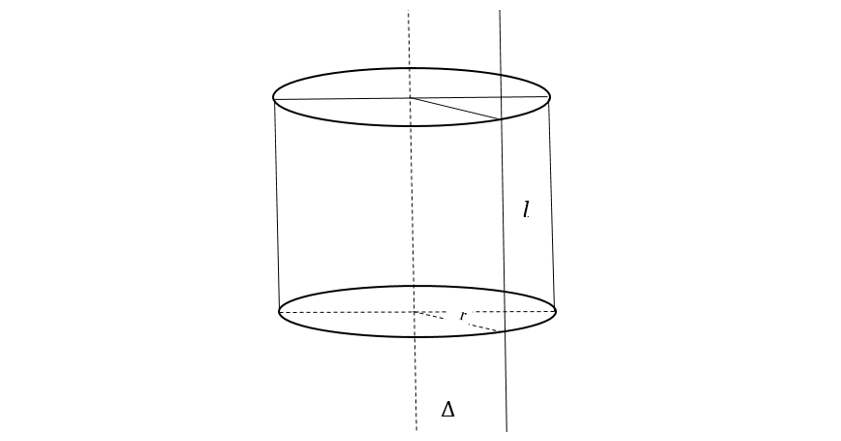
Trong mặt phẳng $(P)$ cho hai đường thẳng $\Delta$ và $l$ song song với nhau, cách nhau một khoảng bằng $r$ . Khi quay mặt phẳng $(P)$ xung quanh $\Delta$ thì đường thẳng $l$ sinh ra một mặt tròn xoay gọi là mặt trụ tròn xoay (gọi tắt là mặt trụ).

Đường thẳng $\Delta$ gọi là trục.
Đường thẳng $l$ gọi là đường sinh.
$r$ là bán kính của mặt trụ đó

3.2 Hình trụ tròn xoay và khối trụ tròn xoay

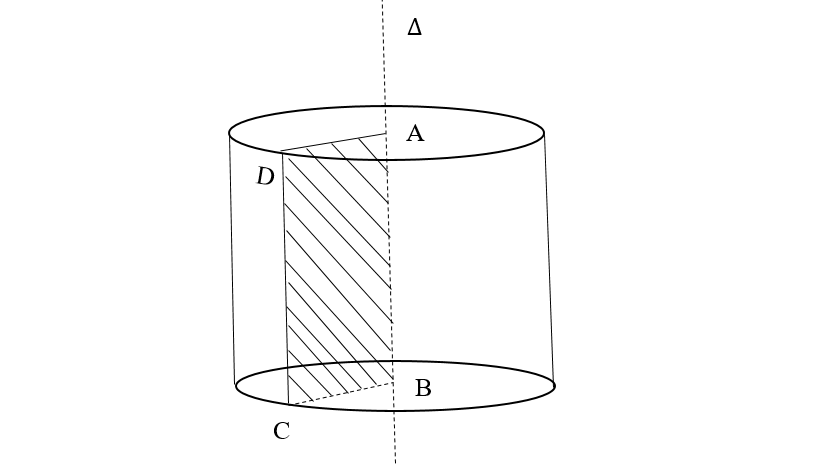
Ta xét hình chữ nhật $ABCD$ . Khi quay hình đó xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh $AB$ , thì đường gấp khúc $ADCB$ tạo thành một hình được gọi là hình trụ tròn xoay (gọi tắt là hình trụ)

Khi quay quanh $AB$ , hai cạnh $AD, BC$ sẽ vạch ra hai hình tròn bằng nhau gọi là hai đáy của hình trụ, bán kính của chúng được gọi là bán kính hình trụ, ví dụ $BC$ hoặc $AD$ .
Độ dài $CD$ gọi là độ dài đường sinh của hình trụ.
Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh $CD$ khi quay quanh $AB$ gọi là mặt xung quanh của hình trụ.
Khoảng cách $AB$ giữa hai mặt phẳng song song chứa hai đáy là chiều cao của hình trụ.

Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó. Khối trụ tròn xoay còn được gọi tắt là khối trụ.

Những điểm không thuộc khối trụ được gọi là những điểm ngoài của khối trụ.
Những điểm thuộc khối trụ được gọi là những điểm ngoài của khối nón.
Ta gọi mặt đáy, chiều cao, đường sinh, bán kính của một hình trụ theo tứ tự là mặt đáy, chiều cao, đường sinh, bán kính của khối trụ tương ứng.

3.3 Công thức tính diện tích hình trụ và thể tích khối trụ

Cho hình trụ có chiều cao là $h$ , bán kính đáy $r$ thì có:

Diện tích xung quanh: $S_{xq}$ = $2\pi rl$ .
Diện tích đáy: $S_{2đ}$ = $2\pi r^{2}$ .
Diện tích toàn phần $S_{tp}=S_{xq}+S_{2đ}=2\pi rl + 2\pi r^{2}$ .
Thể tích khối nón: $V = \pi r^{2}h$ .

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết khái niệm về mặt tròn xoay. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!