Cách tính góc giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng

Ngọc Quốc Tháng Mười 24, 2021

Trong bài viết này, HocThatGioi sẽ giới thiệu đến các bạn cách tình góc giữa 2 đường thẳng trong không gian Oxyz. Đây là dạng bài cơ bản thường xuất hiện dưới dạng trắc nghiệm trong đề thi và là cơ sở để giải được những bài toán khó hơn. Hi vọng bài viết này sẽ giúp phần nào giải quyết được những thắc mắc mà bạn đang vướng phải. Nhớ đọc đến hết bài nhé!

1. Góc giữa 2 đường thẳng trong không gian Oxyz là gì?

Giữa 2 đường thẳng có vị trí khác nhau thì sẽ có cách nhìn góc của chúng khác nhau:

Đối với 2 đường thẳng song song hoặc trùng nhau: Góc tạo thành giữa chúng là 0.
Đối với góc giữa 2 đường thẳng cắt nhau: Ta sẽ tính góc nhọn được tạo thành giữa 2 đường thẳng ấy.
Đối với 2 đường thẳng chéo nhau: thì ta sẽ vẽ một đường thẳng song song và cắt đường còn lại, khi đó, góc nhọn giữa 2 đường thẳng cắt nhau đó sẽ là góc cần tìm. Hoặc ta cũng có thể vẽ 2 đường thẳng song song với 2 đường đó và cắt nhau. Khi đó, góc nhọn giữa 2 đường thẳng vừa vẽ sẽ là góc của 2 đường thẳng ban đầu. Minh họa như hình bên dưới

Cách tính góc giữa 2 đường thẳng trong không gian Oxyz - bài tập áp dụng 2 — Góc giữa 2 đường thẳng trong không gian

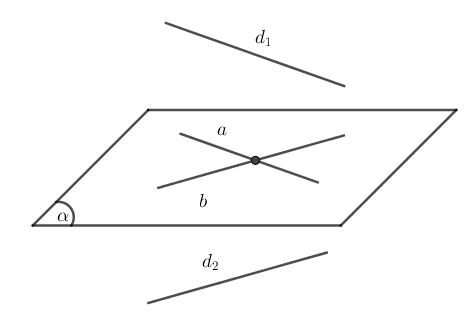
2. Cách tính góc giữa 2 đường thẳng trong không gian Oxyz

Cho 2 đường thẳng $d_1$ có vecto chỉ phương $u_1=(a_1;b_1;c_1)$ và đường thẳng $d_2$ có vecto chỉ phương $u_2=(a_2;b_2;c_2)$ . Khi đó góc $\alpha$ giữa 2 đường thẳng $d_1$ và $d_2$ chính là góc giữa 2 vecto chỉ phương của 2 đường thẳng đó và được tính theo công thức sau:

Công thức tính góc giữa 2 đường thẳng trong không gian:

cos \alpha = \frac{|\vec {d_1} \vec {d_2}|}{|\vec{d_1}| |\vec {d_2}|}= \frac{|a_1a_2+b_1b_2+c_1c_2|}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}

Trong đó:
Đường thẳng

d_1

có vecto chỉ phương

u_1=(a_1;b_1;c_1)

Đường thẳng

d_2

có vecto chỉ phương

u_2=(a_2;b_2;c_2)

Khi có được $cos \alpha$ thì việc tính ra góc $\alpha$ không phải là vấn đề gì khó. Xem thử ví dụ dưới đây để hiểu rõ hơn về cách tính góc giữa 2 đường thẳng trng không gian.

Cho 2 đường thẳng

d_1

và

d_2

có phương trình lần lượt như sau:

d_1: \left\{\begin{matrix} x=t \\ y=-1-t \\ z=1+2t \end{matrix}\right.

d_2 \left\{\begin{matrix} x=-1-t \\ y=t \\ z=3+t \end{matrix}\right.

.
Tính góc giữa 2 đường thẳng trên

cos \alpha = \frac{|\vec {d_1} \vec {d_2}|}{|\vec{d_1}| |\vec {d_2}|}= \frac{|a_1a_2+b_1b_2+c_1c_2|}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}} =0

=> Góc giữa 2 đường thẳng trên là

90^0

3. Bài tập tính góc giữa 2 đường thẳng trong không gian

Thử ngay những bài tập dưới đây để nhớ lâu hơn công thức mà HocThatGioi vừa giới thiệu ở trên nhé!

1. Cho 2 đường thẳng

d_1

và

d_2

có phương trình lần lượt như sau:

d_1: \left\{\begin{matrix} x=-t \\ y=-1+4t \\ z=3t \end{matrix}\right.

d_2 \left\{\begin{matrix} x=t \\ y=-1-4t \\ z=2-3t \end{matrix}\right.

.
Tính góc giữa 2 đường thẳng trên

a. $0^o$
b. $30^o$
c. $60^o$
d. $90^o$

2. Cho 2 đường thẳng

d_1

và

d_2

có phương trình lần lượt như sau:

d_1: \left\{\begin{matrix} x=t \\ y=5-2t \\ z=14-3t \end{matrix}\right.

d_2 \left\{\begin{matrix} x=5-4t \\ y=6+t \\ z=2+5t \end{matrix}\right.

.
Tính góc giữa 2 đường thẳng trên

a. $45^o$
b. $30^o$
c. $60^o$
d. $90^o$

3. Cho 4 điểm

A(1;0;0), B(0;1;0), C(0;0;1),D(-2;1;-1)

. Tính góc giữa 2 đường thẳng AB và CD.

a. $30^o$
b. $60^o$
c. $90^o$
d. $45^o$

4. Cho 2 đường thẳng

d_1

và

d_2

có phương trình lần lượt như sau:

d_1: \left\{\begin{matrix} x=1+2t \\ y=4+2t \\ z=3-t \end{matrix}\right.

d_2 \left\{\begin{matrix} x=t \\ y=-5-2t \\ z=7+t \end{matrix}\right.

.
Tính góc giữa 2 đường thẳng trên

a. $\frac{1}{\sqrt 6}$
b. $\frac{1}{\sqrt 2}$
c. $\frac{1}{\sqrt 3}$
d. 30

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Cách tính góc giữa 2 đường thẳng trong không gian Oxyz. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!