Dạng toán tương giao giữa hình nón và mặt phẳng – hướng dẫn giải và bài tập
Xin chào các bạn, bài học hôm nay HocThatGioi sẽ tiếp tục đem đến cho các bạn một dạng toán về hình nón mà thường xuyên xuất hiện trong các đề thi THPTQG đó là tương giao giữa hình nón và mặt phẳng. Dạng toán này thật sự không dễ dàng với một số bạn. Nhưng hôm nay HocThatGioi sẽ giúp các bạn giải quyết dạng toán điển hình của hình nón này. Hãy theo dõi hết bài viết hôm nay nhé !
1. Phương pháp giả tương giao giữa hình nón và mặt phẳng
Phương giải dạng toán này sẽ tuỳ thuộc vào từng trường hợp mà chúng ta gặp. Sau đây là những trường hợp mà chúng ta thường gặp.
1.1 Trường hợp mặt phẳng đi qua trục của hình nón và cắt mặt nón theo 2 đường sinh
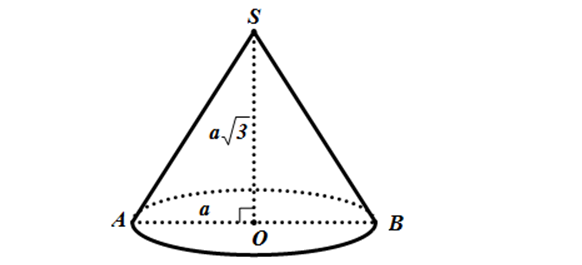
Thiết diện qua trục của hình nón : mặt phẳng (P) đi qua trục của hình nón và cắt mặt nón theo 2 đường sinh
Vậy thiết diện là tam giác cân.
Cách vẽ hình: dưới hình vẽ, thiết diện là tam giác SAB
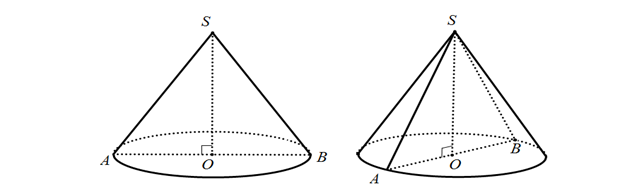
Thiết diện qua trục của hình nón thông thường gặp ở một số dạng như sau :
- Thiết diện qua trục là một tam giác vuông
- Thiết diện qua trục là một tam giác vuông cân
- Thiết diện qua trục là một tam giác đều
- Thiết diện qua trục có góc ở đỉnh bằng số độ cho trước (]60^{\circ} hay 120^{\circ}.)
- ……
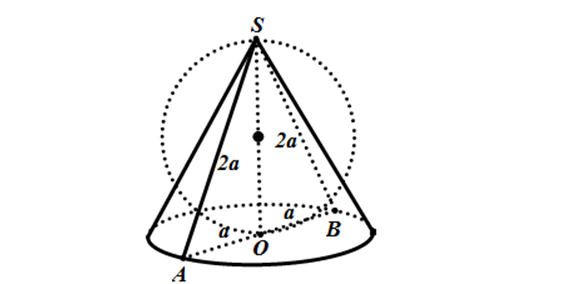
Ví dụ minh hoạ:
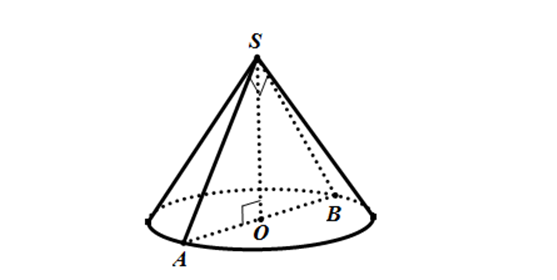
Xét \Delta SAB vuông cân tại S:
SO = AO = \frac{1}{2} AB = \frac{1}{2}.2\sqrt{3} = \sqrt{3} => V = \frac{1}{3}\pi hr^{2} = \frac{1}{3}.SO.\pi.(OA)^{2} = \pi\sqrt{3}
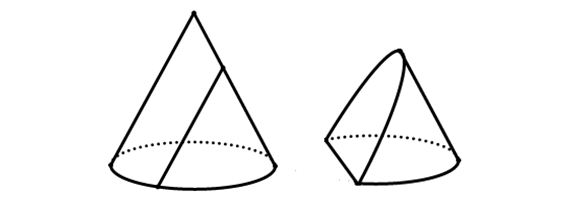
1.2 Trường hợp mặt phẳng đi qua đỉnh của hình nón và cắt mặt nón theo 2 đường sinh
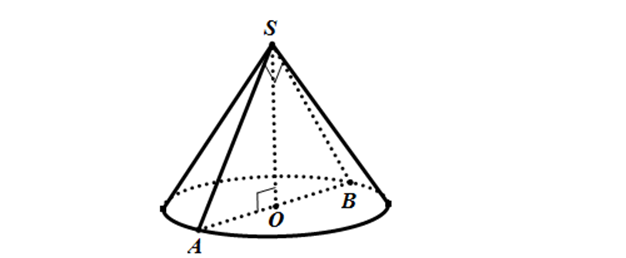
Thiết diện qua đỉnh của hình nón: mặt phẳng P đi qua đỉnh của hình nón và cắt mặt nón theo 2 đường sinh.
Vậy thiết diện cũng là tam giác cân.
Cách vẽ hình: dưới hình vẽ, thiết diện là tam giác SAB
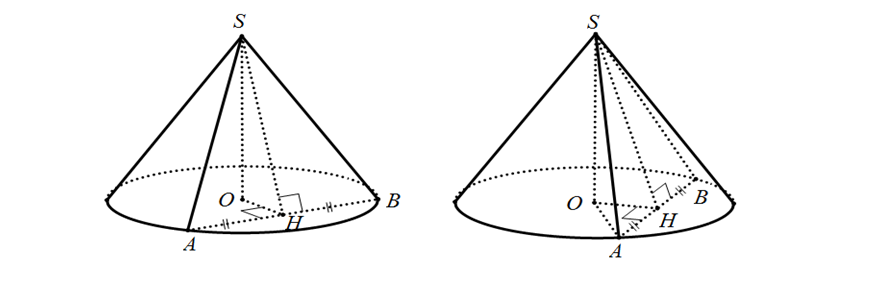
Thiết diện qua đỉnh của hình nón thông thường hay gặp ở một số dạng như sau :
- Thiết diện qua đỉnh là một tam giác vuông
- Thiết diện qua đỉnh là một tam giác vuông cân
- Thiết diện qua đỉnh là một tam giác đều
- Thiết diện qua đỉnh có góc tạo bởi thiết diện và trục là số cho trước (]60^{\circ} hay 120^{\circ}.)
- Thiết diện qua đỉnh của hình nón có khoảng cách từ tâm đáy tới mặt phẳng chứa thiết diện là a (cm)
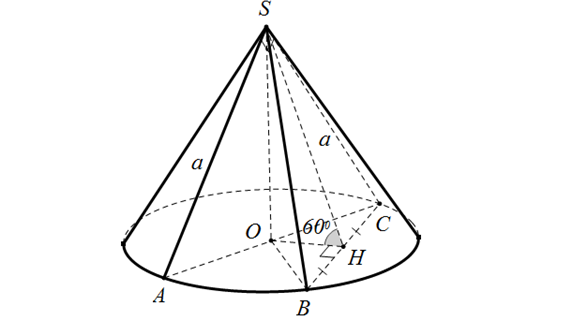
Ví dụ minh hoạ:
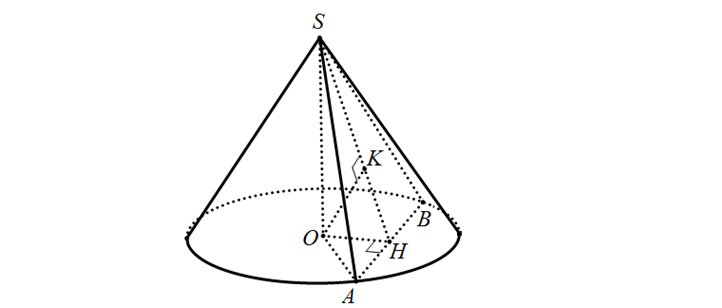
Góc giữa (SAB) và đáy:
(O) \frown (SAB) = AB; (O) : OH \bot AB = H (HA = HB); SH \bot AB = H
Suy ra \widehat{(SAB); (O)} = \widehat {OH; SH} = \widehat{SHO} = 60^{\circ}.
Gỉa thiết cho \Delta SAB đều cạnh 4cm => SH = \frac{4\sqrt{3}}{2} = 2\sqrt{3}
\Delta SOH: sin60^{\circ} = \frac{SO}{SH} => SO = sin60^{\circ}.SH = \sqrt{3}; OH = \frac{SO}{tan60^{\circ}} = \frac{3}{\sqrt{3}}
\Delta OAH: OA = \sqrt{OH^{2} + AH^{2}} = \sqrt{7}
Vậy V = \frac{1}{3}h\pi r^{2} = 7\pi (cm^{3})
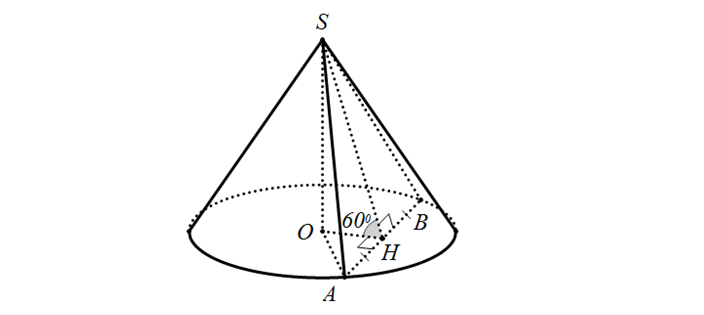
Với ví dụ này, các bạn thường gặp khó khăn ở việc xác định góc giữa hai mặt phẳng, nên HocThatGioi sẽ nhắc lại phần này nhé.
Các bước xác định góc giữa hai mặt phẳng:
- Bước 1: Tìm giao tuyến chung của 2 mặt phẳng
- Bước 2: Lần lượt trên hai mặt phẳng xác định 2 đường thẳng cùng vuông với giao tuyến chung tại một điểm
- Bước 3: Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng vừa tìm
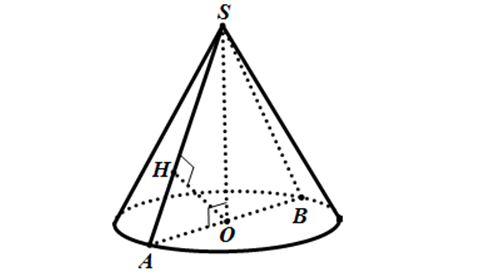
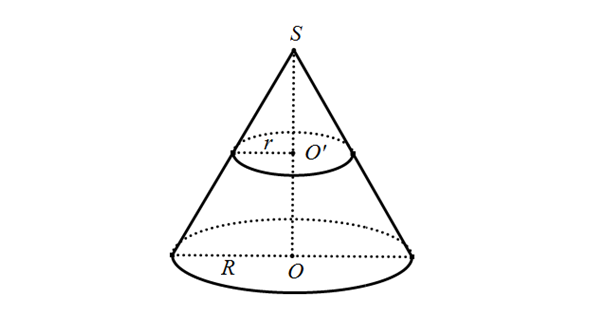
1.3 Trường hợp mặt phẳng vuông góc với trục của hình nón và song song với đường tròn đáy
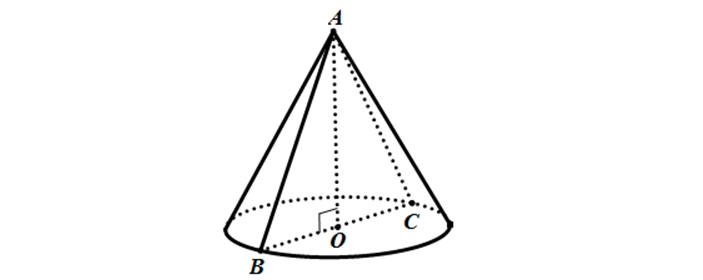
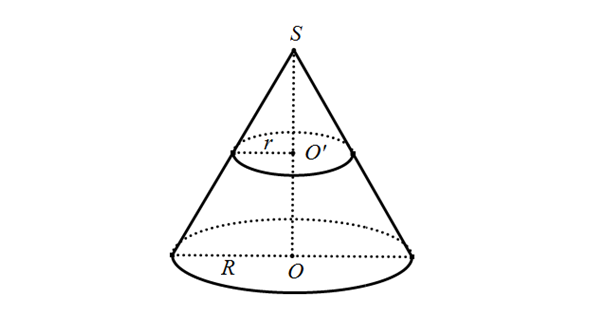
Thiết diện vuông góc với trục của hình nón và song song với đường tròn đáy hình nón: mặt phẳng (P) vuông góc với trục nón.
Vậy giao tuyến là một đường tròn
Cách vẽ: dưới hình vẽ, thiết diện là đường tròn tâm O'.
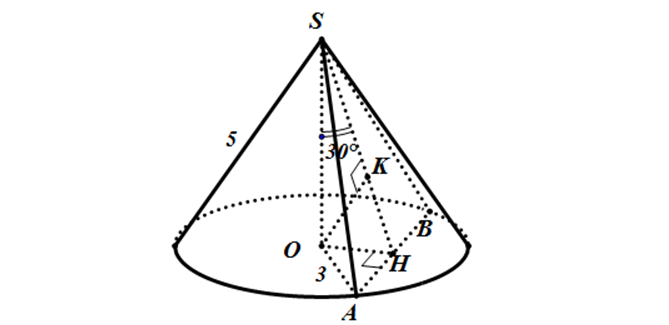
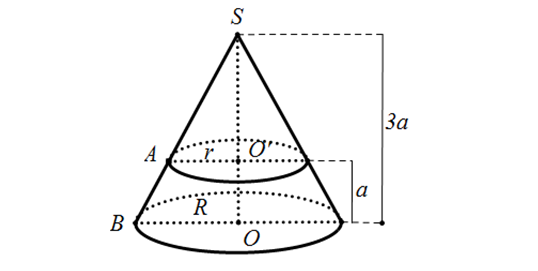
Ví dụ minh hoạ:
Ta có:
S_{O’} = \pi r^{2} = \frac{64}{9}\pi a^{2} => r = \frac{8}{3}a = AO’
Áp dụng Talet trong \Delta SOB, ta có:
\frac{SO’}{SO} = \frac{AO’}{BO} => BO = \frac{SO.AO’}{SO’} = 4a = R
Vậy V = \frac{1}{3}.3a\pi (4a)^{2} = 16\pi a^{3}
1.4 Trường hợp mặt phẳng cắt mọi đường sinh của hình nón
Thiết diện cắt mọi đường sinh của hình nón: mặt phẳng (P) cắt mọi đường sinh hình nón.
Vậy giao tuyến là 1 đường elip.
Cách vẽ hình :
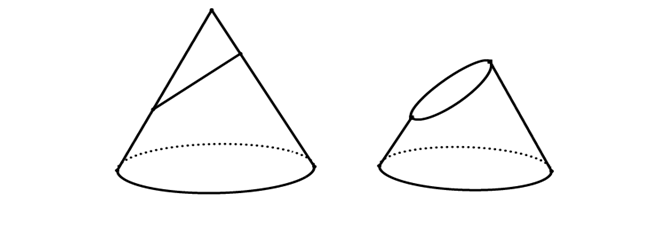
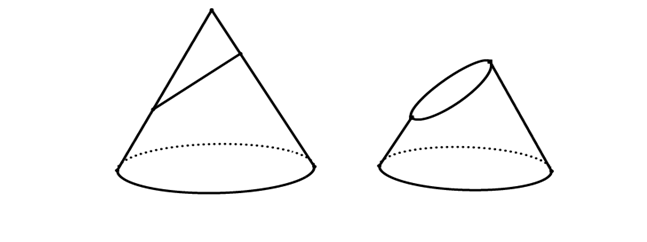
1.5 Trường hợp mặt phẳng song song với 1 đường sinh của hình nón
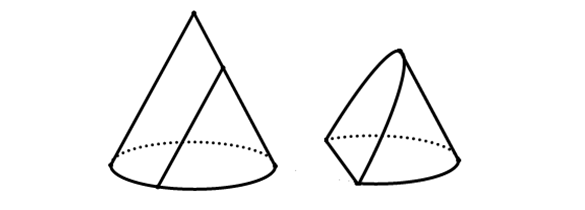
Thiết diện song song với 1 đường sinh của hình nón: mặt phẳng (P) song song với 1 đường sinh hình nón.
Vậy giao tuyến là 1 đường parabol.
Cách vẽ hình:
2. Bài tập tương giao giữa hình nón và mặt phẳng
3. Bài tập tự luyện về sự tương giao giữa hình nón và mặt phẳng
Với bài tập tự luyện, HocThatGioi sẽ đem đến cho các bạn những câu nằm ở mức vận dụng - vận dụng cao, nhưng sẽ có hướng dẫn phương pháp làm cho các bạn nhé.
Trên đây là bài viết về Dạng toán tương giao giữa hình nón và mặt phẳng - hướng dẫn giải và bài tập thành mặt nón, hình nón mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương Mặt tròn xoay để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt.
Bài viết khác liên quan đến Lớp 12 - Toán - Khái niệm mặt tròn xoay
- Lý thuyết mặt nón và mặt trụ hay đầy đủ nhất
- Lý thuyết Hình nón cụt và bài tập chi tiết dễ hiểu nhất
- 20 câu trắc nghiệm bài tập Hình nón dễ hiểu có lời giải chi tiết
- Tổng hợp các câu trắc nghiệm Hình nón vận dụng – vận dụng cao có lời giải
- 20 câu trắc nghiệm bài tập Hình trụ dễ hiểu có lời giải chi tiết nhất
- Tương giao giữa hình trụ và mặt phẳng, đường phẳng
- Dạng toán sự tạo thành mặt trụ, hình trụ – hướng dẫn giải và bài tập
- Dạng toán sự tạo thành mặt nón, hình nón – hướng dẫn giải và bài tập
- Lý thuyết mặt tròn xoay – mặt nón và mặt trụ chi tiết nhất
- Dạng toán mặt cầu ngoại tiếp nội tiếp lăng trụ – hướng dẫn giải và bài tập
- Tổng hợp bài tập hình nón ngoại tiếp nội tiếp có lời giải chi tiết nhất
- Tổng hợp các câu bài tập mặt cầu nội tiếp ngoại tiếp có lời giải chi tiết nhất
- Phương pháp giải hình nón ngoại tiếp nội tiếp hình chóp chi tiết nhất
- Phương pháp giải hình nón ngoại tiếp nội tiếp hình trụ chi tiết nhất