Phương pháp giải các dạng toán phép đối xứng trục cực hay
Xin chào các bạn, bài học hôm nay sẽ đem đến cho các bạn các phương pháp để giải nhưng dạng toán của phép đối xứng trục đầy đủ nhất. Hãy theo dõi hết bài viết cùng HocThatGioi nhé.
1. Xác định ảnh của một hình qua phép đối xứng trục
Phương pháp: Sử dụng biểu thức toạ độ của phép đối xứng trục.
Trong mặt phẳng Oxy, với mỗi điểm M(x;y), gọi M'(x';y') = Đ_{đ}(M).
Nếu chọn d là trục Ox thì \left\{\begin{matrix}x' = x\\y' = -y\end{matrix}\right.
Nếu chọ d là trục Oy, thì \left\{\begin{matrix}x' = - x\\y' = y\end{matrix}\right.
a. Tìm ảnh của M, d, (C) qua phép đối xứng trục Ox
b. Tìm ảnh của M qua phép đối xứng qua đường thẳng d
Gọi M’, d’, (C’) theo thứ tự là ảnh của M, d, (C) qua phép đối xứng trụ Đ_{Ox}
Áp dụng biểu thức toạ độ của phép đối xứng trục Ox, suy ra M'(1;-5).
Tìm ảnh của đường thẳng d:
Lấy N(x;y) \in d \Rightarrow x + 2y + 4 = 0 (1)
Gọi N'(x’;y’) là ảnh của N qua phép đối xứng Đ_{Ox}
Ta có: \left\{\begin{matrix}x’ = x \\ y’ = -y\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = x’\\y = -y’\end{matrix}\right.
Thay (1) ta được: x’ – 2y’ + 4 = 0
Vậy d’: x – 2y + 4 = 0
Tìm ảnh của đường tròn (C)
Đường tròn (C) có tâm I(-1;2) và bán kính R = 3.
Gọi I’, R’ là tâm và bán kính của (C’) thì I'(-1;-2) và R’ = R = 3
Do đó (C’): (x + 1)^{2} + (y + 2)^{2} = 9
b. Tìm ảnh của M qua phép đối xứng qua đường thẳng d
Đường thẳng d_{1} đi qua M vuông góc với d có phương trình 2x – y + 3 = 0
Gọi I = d \cap d_{1} thì toạ độ điểm I là nghiệm của hệ phương trình \left\{\begin{matrix}x + 2y + 4 = 0\\2x – y + 3 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -2\\y = -1\end{matrix}\right. \Rightarrow I(-2;-1)
Gọi M’ đối xứng với M qua d thì I là trung điểm của MM’
Ta có \left\{\begin{matrix}x_{I} = \frac{x_{M} + x_{M’}}{2}\\y_{I} = \frac{y_{M} + y_{M’}}{2}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M’} = 2x_{I} – x_{M} = -5\\y_{M’} = 2y_{I} – y_{M} = -7\end{matrix}\right. \Rightarrow M'(-5;-7)
Vậy ảnh của M qua phép đối xứng đường thẳng d là điểm M'(-5;-7)
Ta có d_{1} \cap d = I(1;1) nên Đ_{d}(I) = I
Lấy M(3;0) \in d_{1}.
Đường thẳng d_{2} đi qua M vuông góc với d có phương trình x – y – 3 = 0.
Gọi M_{0} = d \cap d_{2}, thì toạ độ của M_{0} là nghiệm của hệ \left\{\begin{matrix}x + y – 2 = 0\\x – y – 3 = 0\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = \frac{5}{2}\\y = -\frac{1}{2}\end{matrix}\right.
M_{0}(\frac{5}{2};-\frac{1}{2})
Gọi M’ là ảnh M qua Đ_{d} thì M_{0} là trung điểm MM’ nên M'(2;-1)
Gọi d_{1}’ = Đ_{d}(d_{1}) thì d_{1}’ đi qua I và M’ nên có phương trình \frac{x – 1}{1} = \frac{y – 1}{-2} \Leftrightarrow 2x + y – 3 = 0
Vậy d_{1}’: 2x + y – 3 = 0
2. Dùng phép đối xứng để giải các dạng toán dựng hình
Phương pháp: Để dựng một điểm M ta tìm cách xác định nó như là ảnh của một điểm đã biết qua một phép đối xứng trục, hoặc xem M như là giao điểm của một đường cố định và một với ảnh của một đường đã biết qua phép đối xứng trục.
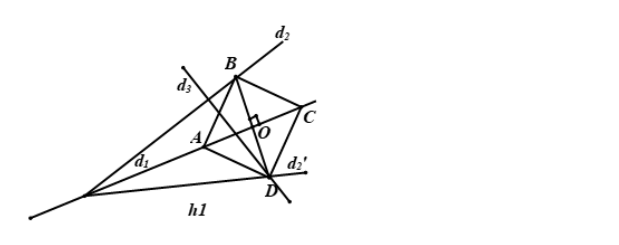
Gỉa sử đã dựng được hình vuông ABCD thoả điều kiện bài toán.
Do A, C \in d_{1} và AC là trục đối xùng của hình vuông ABCD, mặc khác B \in d_{2} nên D \in d_{2}’, trong đó d_{2}’ là đường thẳng đối xứng với d_{2} qua d_{1}. Suy ra D = d_{2}’ \cap d_{3}. Hai điểm B, D đối xứng qua đường thẳng d_{1} nên Đ_{d_{1}}(D) = B.
Cách dựng:
+ Dựng d_{2}’ = Đ_{d_{1}}(d_{2}), gọi D = d_{3} \cap d_{2}’
+ Dựng đường thẳng D vuông góc d_{1} tại O cắt d_{2} tại B.
+ Dựng đường tròn tâm O bán kính BD cắt d_{1} tại A, C (A,C theo thứ tự tạo thành tứ giác ABCD)
Chứng minh: Từ cách dựng suy ra ABCD là hình vuông
Nhận xét:
Trường hợp 1: d_{2} cắt d_{3} khi đó
+ Nếu d_{2}’ \cap d_{3} thì bào toán có một nghiệm hình
+ Nếu d_{2}’ || d_{3} thì bài toán vô nghiệm hình.
Trường hợp 2: d_{2} || d_{3} khi đó:
+ Nếu d_{1} song song và cách đều d_{2}, d_{3} thì bài toán có vô số nghiệm hình
+ Nếu d_{1} hợp với d_{2}, d_{3} một góc 45^{\circ} thì bào toán có một nghiệm hình
+ Nếu d_{1} song song và không cách đều d_{2}, d_{3} hoặc d_{1} không hợp d_{2}, d_{3} một góc 45^{\circ} thì ví dụ đã cho vô nghiệm hình.
3. Dùng phép đối xứng trục để giải các bài tập hợp điểm
Phương pháp: Nếu M' = Đ_{d}(M) với M di động trên hình (H) thì M' di đông trên hình (H') là ảnh của hình (H) qua phép đối xứng trục d.
Ta có: \widehat{A’CA} = \widehat{xAM} = \widehat{ABM} = \widehat{BB’A’} do đó ABB’C là hình thang cân.
Gọi d là trục đối xứng của hình thang này thì Đ_{d}(C) = B’ mà V di động trên đường tròn (O’) nên B’ di động trên đường tròn (O”) là ảnh của (O’) qua Đ_{d}
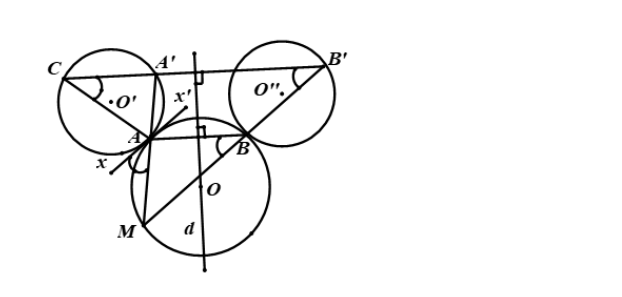
Cảm ơn các bạn đã theo dõi bài viết về Phương pháp giải các dạng toán phép đối xứng trục cực hay của HocThatGioi. Nếu thấy bài viết hay, ý nghĩa hãy chia sẻ nó đến với bạn bè và nhớ theo dõi HocThatGioi mỗi ngày để cập nhật thêm những kiến thức mới mỗi ngày nhé! Chúc các bạn học tốt!





